Czegóż dawniej uczono
Twierdzenie Sturma
Rozważamy wielomian 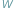 o współczynnikach rzeczywistych stopnia
o współczynnikach rzeczywistych stopnia 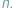 Wiadomo, że wielomian taki ma
Wiadomo, że wielomian taki ma 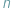 pierwiastków zespolonych; niektóre z nich (czasami wszystkie) są, być może, rzeczywiste. Twierdzenie Sturma pozwala obliczyć liczbę pierwiastków rzeczywistych wielomianu
pierwiastków zespolonych; niektóre z nich (czasami wszystkie) są, być może, rzeczywiste. Twierdzenie Sturma pozwala obliczyć liczbę pierwiastków rzeczywistych wielomianu 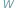 należących do wybranego przedziału
należących do wybranego przedziału 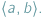 Oczywiście, odpowiedź na to pytanie możemy uzyskać, stosując metodę badania funkcji wielomianowej
Oczywiście, odpowiedź na to pytanie możemy uzyskać, stosując metodę badania funkcji wielomianowej 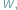 znaną z analizy matematycznej. Metoda Sturma jest czysto algebraiczna, nie stosuje metod analizy matematycznej.
znaną z analizy matematycznej. Metoda Sturma jest czysto algebraiczna, nie stosuje metod analizy matematycznej.
Sprecyzujmy założenia. Wielomian 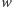 o współczynnikach rzeczywistych nie ma pierwiastków wielokrotnych (gdyby miał, to możemy je usunąć opisaną w Delcie 12/2015 metodą) oraz dla ustalonych liczb
o współczynnikach rzeczywistych nie ma pierwiastków wielokrotnych (gdyby miał, to możemy je usunąć opisaną w Delcie 12/2015 metodą) oraz dla ustalonych liczb 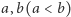 wartości
wartości 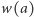 i
i 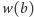 są różne od zera.
są różne od zera.
Ciągiem Sturma dla wielomianu 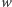 nazywamy ciąg wielomianów
nazywamy ciąg wielomianów 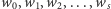 określony przez algorytm Euklidesa dla wielomianu
określony przez algorytm Euklidesa dla wielomianu 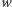 i jego pochodnej
i jego pochodnej 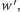 zmodyfikowany w ten sposób, że rozważamy kolejne reszty z dzielenia zaopatrzone w znak minus:
zmodyfikowany w ten sposób, że rozważamy kolejne reszty z dzielenia zaopatrzone w znak minus:
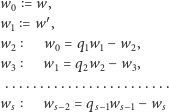
dotąd aż wielomian 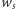 nie będzie miał pierwiastków w przedziale
nie będzie miał pierwiastków w przedziale 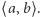 Ten warunek na pewno możemy spełnić, gdyż zmodyfikowany algorytm Euklidesa, który tu stosujemy, prowadzi do największego wspólnego dzielnika wielomianu
Ten warunek na pewno możemy spełnić, gdyż zmodyfikowany algorytm Euklidesa, który tu stosujemy, prowadzi do największego wspólnego dzielnika wielomianu 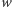 i jego pochodnej, a gdyby ten miał pierwiastek, to byłby to wspólny pierwiastek
i jego pochodnej, a gdyby ten miał pierwiastek, to byłby to wspólny pierwiastek 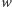 i
i 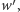 czyli pierwiastek wielokrotny wielomianu
czyli pierwiastek wielokrotny wielomianu 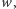 wbrew założeniu, że nie ma pierwiastków wielokrotnych.
wbrew założeniu, że nie ma pierwiastków wielokrotnych.
Dla  należącego do
należącego do 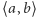 przez
przez 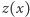 oznaczamy liczbę zmian znaku w ciągu
oznaczamy liczbę zmian znaku w ciągu 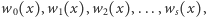 tj. liczbę takich sytuacji, gdy kolejne wyrazy są liczbami przeciwnych znaków, a jeśli któryś wyraz jest zerowy, to pomijamy go i porównujemy znaki pozostałych wyrazów sąsiednich.
tj. liczbę takich sytuacji, gdy kolejne wyrazy są liczbami przeciwnych znaków, a jeśli któryś wyraz jest zerowy, to pomijamy go i porównujemy znaki pozostałych wyrazów sąsiednich.
Twierdzenie 1 (Sturma). Liczba pierwiastków rzeczywistych wielomianu 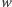 spełniającego sformułowane wyżej założenia w przedziale
spełniającego sformułowane wyżej założenia w przedziale 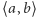 jest równa
jest równa 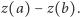
Dowód. Dwa kolejne wielomiany ciągu Sturma nie mogą mieć wspólnego miejsca zerowego w przedziale 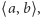 gdyby bowiem
gdyby bowiem 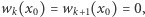 to wobec równości
to wobec równości
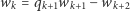
mielibyśmy 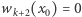 i kolejne wielomiany ciągu Sturma aż do
i kolejne wielomiany ciągu Sturma aż do 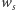 zerowałyby się w punkcie
zerowałyby się w punkcie 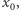 co nie jest możliwe.
co nie jest możliwe.
Wszystkie wielomiany ciągu Sturma mają skończoną liczbę miejsc zerowych, możemy więc dany przedział 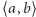 podzielić na skończoną liczbę podprzedziałów, w których każdy z wielomianów ma stały znak. Funkcja
podzielić na skończoną liczbę podprzedziałów, w których każdy z wielomianów ma stały znak. Funkcja  jest stała w każdym z tych podprzedziałów i może zmieniać swą wartość tylko przy przejściu przez punkt, w którym zeruje się jeden z wielomianów ciągu Sturma.
jest stała w każdym z tych podprzedziałów i może zmieniać swą wartość tylko przy przejściu przez punkt, w którym zeruje się jeden z wielomianów ciągu Sturma.
Jeśli 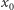 jest miejscem zerowym wielomianu
jest miejscem zerowym wielomianu 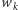 dla
dla 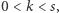 to ponieważ
to ponieważ
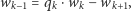
więc liczby 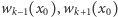 mają przeciwne znaki. W pobliżu punktu
mają przeciwne znaki. W pobliżu punktu 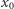 na lewo i na prawo możliwe są następujące układy znaków liczb
na lewo i na prawo możliwe są następujące układy znaków liczb 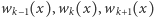 :
:
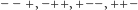
a w samym punkcie 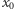 :
:
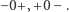
W każdym przypadku mamy tylko jedną zmianę znaku. Jeśli więc 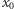 nie jest miejscem zerowym wielomianu
nie jest miejscem zerowym wielomianu 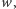 to przy przejściu przez
to przy przejściu przez 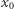 funkcja
funkcja  nie zmienia swej wartości. Jeśli natomiast
nie zmienia swej wartości. Jeśli natomiast 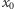 jest miejscem zerowym wielomianu
jest miejscem zerowym wielomianu 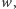 to
to
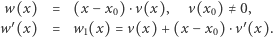
Ponieważ 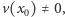 więc w pewnym otoczeniu
więc w pewnym otoczeniu 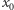 funkcja
funkcja  ma stały znak. Gdy
ma stały znak. Gdy 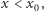 funkcja
funkcja 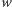 ma przeciwny znak niż
ma przeciwny znak niż 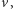 gdy zaś
gdy zaś 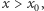 funkcje
funkcje 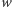 i
i  mają ten sam znak. Zatem funkcja
mają ten sam znak. Zatem funkcja  przy przejściu przez
przy przejściu przez 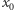 zmniejsza swą wartość o 1. Liczba pierwiastków rzeczywistych wielomianu
zmniejsza swą wartość o 1. Liczba pierwiastków rzeczywistych wielomianu 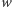 leżących w przedziale
leżących w przedziale 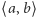 jest istotnie równa
jest istotnie równa 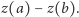

Przykład 1. Wyznaczymy liczbę pierwiastków rzeczywistych wielomianu 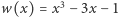 i wskażemy takie przedziały o końcach w liczbach całkowitych, z których każdy zawiera tylko jeden z tych pierwiastków.
i wskażemy takie przedziały o końcach w liczbach całkowitych, z których każdy zawiera tylko jeden z tych pierwiastków.
Zamiast pochodnej 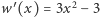 możemy przyjąć
możemy przyjąć 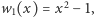 gdyż przy wyznaczaniu liczby zmian znaku ważne są tylko znaki wartości wielomianów ciągu Sturma. Obliczamy
gdyż przy wyznaczaniu liczby zmian znaku ważne są tylko znaki wartości wielomianów ciągu Sturma. Obliczamy 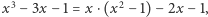 więc przyjmujemy
więc przyjmujemy 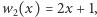 a ponieważ
a ponieważ 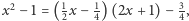 więc
więc 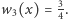 Budujemy tabelkę, w której pierwszym wierszu wypisujemy wybrane liczby całkowite - będą one końcami przedziałów, w których spodziewamy się pierwiastków wielomianu
Budujemy tabelkę, w której pierwszym wierszu wypisujemy wybrane liczby całkowite - będą one końcami przedziałów, w których spodziewamy się pierwiastków wielomianu 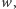 a w pierwszej kolumnie wypisujemy wielomiany ciągu Sturma. Pod każdą liczbą z pierwszego wiersza wypisujemy znaki kolejnych wielomianów, a niżej liczbę zmian znaku.
a w pierwszej kolumnie wypisujemy wielomiany ciągu Sturma. Pod każdą liczbą z pierwszego wiersza wypisujemy znaki kolejnych wielomianów, a niżej liczbę zmian znaku.

Z tabeli odczytujemy, że po jednym pierwiastku wielomianu 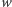 zawiera każdy z przedziałów
zawiera każdy z przedziałów 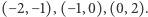 Są to oczywiście wszystkie pierwiastki, gdyż wielomian stopnia trzeciego nie ma więcej niż trzy pierwiastki.
Są to oczywiście wszystkie pierwiastki, gdyż wielomian stopnia trzeciego nie ma więcej niż trzy pierwiastki.
Przykład 2. Rozważmy teraz wielomian 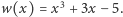 Jako
Jako 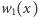 możemy przyjąć
możemy przyjąć 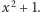 Ponieważ
Ponieważ 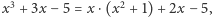 więc przyjmujemy
więc przyjmujemy 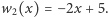 Następnie obliczamy
Następnie obliczamy 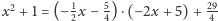 ; zatem
; zatem 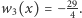 Budujemy tabelkę podobną, jak w poprzednim przykładzie, ale zaczniemy od wyznaczenia znaków granic wielomianów ciągu Sturma w
Budujemy tabelkę podobną, jak w poprzednim przykładzie, ale zaczniemy od wyznaczenia znaków granic wielomianów ciągu Sturma w 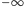 i
i 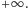
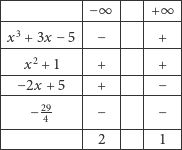
Wynika stąd, że wielomian 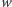 ma tylko jeden pierwiastek rzeczywisty. Obliczmy liczbę zmian znaku na końcach przedziału
ma tylko jeden pierwiastek rzeczywisty. Obliczmy liczbę zmian znaku na końcach przedziału 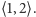
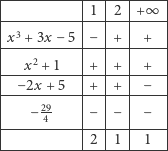
Jedyny pierwiastek wielomianu 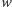 należy do przedziału
należy do przedziału