Czegóż dawniej uczono
Pierwiastki wielokrotne wielomianu
Rozważamy wielomian 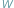 stopnia
stopnia 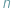 o współczynnikach rzeczywistych...
o współczynnikach rzeczywistych...

Liczba 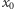 jest pierwiastkiem wielomianu
jest pierwiastkiem wielomianu 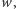 jeśli wielomian ten jest podzielny przez dwumian
jeśli wielomian ten jest podzielny przez dwumian 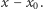 Pierwiastek
Pierwiastek 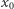 jest
jest 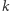 -krotny (
-krotny ( 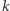 jest pewną liczbą naturalną), jeśli wielomian
jest pewną liczbą naturalną), jeśli wielomian 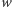 jest podzielny przez
jest podzielny przez 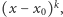 ale nie dzieli się przez
ale nie dzieli się przez 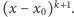 Na przykład dla wielomianu
Na przykład dla wielomianu 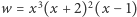 pierwiastek
pierwiastek 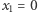 jest trzykrotny,
jest trzykrotny, 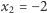 jest dwukrotny,
jest dwukrotny, 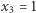 jest jednokrotny.
jest jednokrotny.
Do badania krotności pierwiastków wielomianu wygodnie jest posłużyć się pochodną tego wielomianu. Na wykładzie algebry nie odwoływano się do definicji pochodnej znanej z analizy matematycznej, a określano pochodną jednomianu 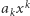 w sposób formalny, jako
w sposób formalny, jako 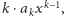 pochodną jednomianu stopnia zero
pochodną jednomianu stopnia zero 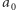 jako 0, a pochodną wielomianu będącego sumą jednomianów jako sumę pochodnych tych jednomianów. Na przykład
jako 0, a pochodną wielomianu będącego sumą jednomianów jako sumę pochodnych tych jednomianów. Na przykład

Można udowodnić, że pochodna określona w sposób formalny dla wielomianu ma wiele własności przysługujących pochodnej funkcji znanych z analizy matematycznej, w szczególności pochodna iloczynu wielomianów 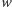 i
i  spełnia związek
spełnia związek 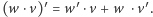
Twierdzenie. Jeśli liczba jest pierwiastkiem 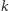 -krotnym wielomianu
-krotnym wielomianu 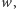 to jest pierwiastkiem
to jest pierwiastkiem 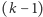 -krotnym pochodnej
-krotnym pochodnej 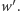
Dowód. Ponieważ 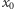 jest pierwiastkiem
jest pierwiastkiem 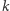 -krotnym wielomianu
-krotnym wielomianu 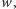 więc
więc 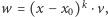 przy czym
przy czym 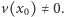 Wobec tego
Wobec tego
![w′ = k(x− x0)k−1⋅v +(x − x0)k⋅v′= (x − x0)k−1[k ⋅v + (x −x0) ⋅v′].](/math/temat/matematyka/algebra/2015/11/29/Pierwiastki_wielokrotne_wielomia/17x-55556d0a99d7cdcbd22c23c6035e6f9ccc346751-dm-33,33,33-FF,FF,FF.gif)
Liczba 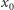 nie jest pierwiastkiem wielomianu występującego w nawiasie kwadratowym, gdyż jest pierwiastkiem drugiego składnika, ale nie jest pierwiastkiem składnika pierwszego. Wynika stąd, że jest ona pierwiastkiem
nie jest pierwiastkiem wielomianu występującego w nawiasie kwadratowym, gdyż jest pierwiastkiem drugiego składnika, ale nie jest pierwiastkiem składnika pierwszego. Wynika stąd, że jest ona pierwiastkiem 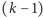 -krotnym pochodnej
-krotnym pochodnej 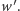
Wniosek 1. Liczba 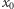 jest pierwiastkiem wielokrotnym wielomianu
jest pierwiastkiem wielokrotnym wielomianu  wtedy i tylko wtedy, gdy jest wspólnym pierwiastkiem tego wielomianu i jego pochodnej, a zatem jest pierwiastkiem największego wspólnego dzielnika
wtedy i tylko wtedy, gdy jest wspólnym pierwiastkiem tego wielomianu i jego pochodnej, a zatem jest pierwiastkiem największego wspólnego dzielnika 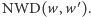
Wniosek 2. Dzieląc wielomian 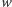 przez
przez 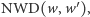 otrzymamy wielomian mający te same pierwiastki, co wielomian
otrzymamy wielomian mający te same pierwiastki, co wielomian 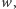 ale wszystkie jednokrotne.
ale wszystkie jednokrotne.
Dowód. Istotnie, jeśli 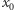 jest pierwiastkiem
jest pierwiastkiem 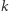 -krotnym wielomianu
-krotnym wielomianu 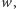 to jest pierwiastkiem
to jest pierwiastkiem 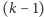 -krotnym pochodnej
-krotnym pochodnej 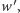 jest więc też pierwiastkiem
jest więc też pierwiastkiem 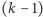 -krotnym wielomianu
-krotnym wielomianu 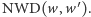 Dzielenie
Dzielenie 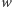 przez
przez 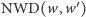 możemy nazywać usuwaniem pierwiastków wielokrotnych.
możemy nazywać usuwaniem pierwiastków wielokrotnych.
Przykład. Usuniemy pierwiastki wielokrotne wielomianu

Obliczamy pochodną 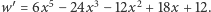 Aby obliczyć
Aby obliczyć 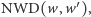 zastosujemy algorytm Euklidesa, zastępując wielomian
zastosujemy algorytm Euklidesa, zastępując wielomian 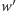 proporcjonalnym do niego wielomianem
proporcjonalnym do niego wielomianem 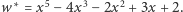 Najpierw dzielimy
Najpierw dzielimy 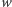 przez
przez 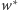 z resztą i dostajemy
z resztą i dostajemy

a następnie dzielimy 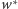 przez
przez 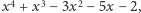 otrzymując iloraz
otrzymując iloraz 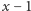 i resztę 0. Wobec tego
i resztę 0. Wobec tego 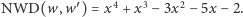 Po podzieleniu wielomianu
Po podzieleniu wielomianu 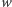 przez otrzymany wielomian stopnia 4 otrzymamy
przez otrzymany wielomian stopnia 4 otrzymamy 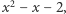 czyli
czyli 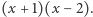 Zatem liczby
Zatem liczby 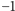 i
i 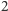 są pierwiastkami wielomianu
są pierwiastkami wielomianu 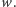 Można łatwo sprawdzić, że
Można łatwo sprawdzić, że 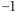 jest pierwiastkiem czterokrotnym, a 2 - pierwiastkiem dwukrotnym.
jest pierwiastkiem czterokrotnym, a 2 - pierwiastkiem dwukrotnym.