Okręgi Carlyle’a
Jednym z najstarszych zagadnień matematyki są równania algebraiczne, wśród nich problem znalezienia pierwiastków trójmianu kwadratowego...
Już w starożytności pojawiły się zadania, do rozwiązania których należało wyciągnąć pierwiastek kwadratowy z liczby (to jest rozwiązać równanie 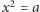 dla
dla 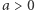 ) lub odnaleźć miejsce zerowe trójmianu kwadratowego. Pojawił się, między innymi, klasyczny problem wyznaczenia długości przekątnej kwadratu (oraz wykazanie niewspółmierności przekątnej z bokiem). Jedne z pierwszych zapisków zawierających rozwiązania równań kwadratowych oraz sześciennych pochodzą jeszcze z czasów Babilonii, datowane są na 1800-1600) p.n.e. Dopiero prawie 3000 lat później, w XII wieku Aczarja Bhaskara wykazał, że liczba dodatnia ma dwa pierwiastki.
) lub odnaleźć miejsce zerowe trójmianu kwadratowego. Pojawił się, między innymi, klasyczny problem wyznaczenia długości przekątnej kwadratu (oraz wykazanie niewspółmierności przekątnej z bokiem). Jedne z pierwszych zapisków zawierających rozwiązania równań kwadratowych oraz sześciennych pochodzą jeszcze z czasów Babilonii, datowane są na 1800-1600) p.n.e. Dopiero prawie 3000 lat później, w XII wieku Aczarja Bhaskara wykazał, że liczba dodatnia ma dwa pierwiastki.
Wiele problemów algebraicznych można rozwiązać w sposób dokładny lub przybliżony, wykorzystując narzędzia geometrii. Historia zna wiele przykładów, począwszy od problemu kwadratury koła, przez rozwiązywanie równań oraz układów równań liniowych. Takie graficzne (i dokładne) rozwiązanie jest również możliwe dla równań kwadratowych. Rozwiązanie graficzne wykorzystuje jedynie klasyczne konstrukcje oparte na cyrklu i linijce - oraz tytułowe okręgi Carlyle'a.
Rozważmy równanie kwadratowe:
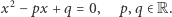 |
(1) |
Naszym celem jest znalezienie rozwiązań powyższego równania, za pomocą pewnej konstrukcji geometrycznej. Oczywiście, algebraicznie jesteśmy w stanie natychmiast podać pierwiastki równania (1):

Jedną z metod przybliżonego poszukiwania pierwiastków jest próba narysowania paraboli. Zwykle jednak do tego celu wykorzystujemy właśnie pierwiastki równania. Tego błędnego koła można szczęśliwie uniknąć, wykorzystując wspomniane już okręgi Carlyle'a.

Wprowadźmy formalną definicję.
Definicja. Okręgiem Carlyle'a stowarzyszonym z równaniem kwadratowym (1) nazywamy okrąg, którego średnicą jest odcinek o końcach w punktach 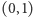 oraz
oraz 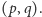
Okrąg Carlyle'a jest wyznaczony w sposób jednoznaczny przez równanie (1). Co więcej, łatwo można zaobserwować, że dla każdego okręgu przechodzącego przez punkt 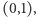 istnieją takie wartości współczynników
istnieją takie wartości współczynników 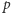 oraz
oraz 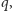 że okrąg ten jest okręgiem Carlyle'a stowarzyszonym z równaniem kwadratowym
że okrąg ten jest okręgiem Carlyle'a stowarzyszonym z równaniem kwadratowym 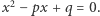
Najważniejszą cechą okręgu Carlyle'a jest jego związek z pierwiastkami równania, które wyznacza okrąg. Okazuje się bowiem, że liczba 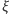 jest rozwiązaniem równania (1) wtedy i tylko wtedy, gdy stowarzyszony okrąg Carlyle'a przecina oś odciętych w punkcie
jest rozwiązaniem równania (1) wtedy i tylko wtedy, gdy stowarzyszony okrąg Carlyle'a przecina oś odciętych w punkcie 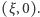 Istotnie, środek takiego okręgu to punkt o współrzędnych
Istotnie, środek takiego okręgu to punkt o współrzędnych 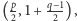 a z twierdzenia Pitagorasa jego promień jest równy
a z twierdzenia Pitagorasa jego promień jest równy 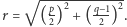 Okrąg Carlyle'a opisany jest więc równaniem
Okrąg Carlyle'a opisany jest więc równaniem
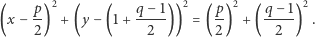 |
(2) |
Ponieważ poszukujemy punktów przecięcia okręgu z osią 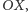 więc podstawiamy
więc podstawiamy 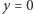 do równania (2). Upraszcza się ono do postaci
do równania (2). Upraszcza się ono do postaci
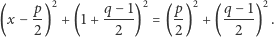 |
(3) |
Po redukcji równania (3) otrzymujemy dokładnie równanie (1).
Należy ponadto sprawdzić, że okrąg przecina oś 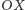 w co najmniej jednym punkcie wtedy i tylko wtedy, gdy wyróżnik trójmianu (1) jest nieujemny. Można to zrobić niezależnie od powyższego rozumowania i to zadanie pozostawiamy Tobie, Drogi Czytelniku.
w co najmniej jednym punkcie wtedy i tylko wtedy, gdy wyróżnik trójmianu (1) jest nieujemny. Można to zrobić niezależnie od powyższego rozumowania i to zadanie pozostawiamy Tobie, Drogi Czytelniku.
Dzięki swoim własnościom okręgi Carlyle'a znalazły zastosowanie w konstrukcjach wielokątów foremnych. W szczególności za ich pomocą, wykorzystując wyłącznie cyrkiel i linijkę, można łatwo skonstruować pięciokąt oraz siedemnastokąt foremny.
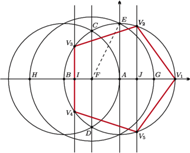
Opiszemy teraz konstrukcję pięciokąta foremnego z wykorzystaniem okręgów Carlyle'a.
- Narysuj okrąg (zwany dalej: początkowym) o środku w punkcie
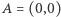 oraz promieniu
oraz promieniu 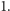 Niech ponadto
Niech ponadto 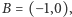
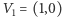 oraz
oraz 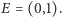 Punkt
Punkt 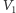 jest jednym z wierzchołków konstruowanego pięciokąta foremnego.
jest jednym z wierzchołków konstruowanego pięciokąta foremnego. - Narysuj okrąg o środku w punkcie
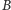 przechodzący przez punkt
przechodzący przez punkt 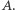 Okrąg ten przecina okrąg początkowy w punktach
Okrąg ten przecina okrąg początkowy w punktach 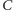 oraz
oraz 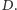
- Przez punkty
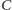 oraz
oraz 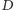 poprowadź prostą. Punkt jej przecięcia z osią
poprowadź prostą. Punkt jej przecięcia z osią 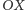 oznacz
oznacz 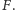
- Narysuj okrąg o środku w punkcie
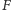 przechodzący przez punkt
przechodzący przez punkt 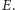 Przecina on oś
Przecina on oś 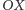 w dwóch punktach
w dwóch punktach 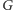 oraz
oraz 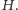
- Skonstruuj symetralne odcinków
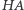 oraz
oraz 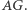 Oznacz miejsca przecięcia tych symetralnych z osią
Oznacz miejsca przecięcia tych symetralnych z osią 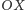 odpowiednio przez
odpowiednio przez 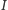 oraz
oraz 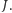
- Symetralne skonstruowane w punkcie 5. przecinają ponadto okrąg początkowy w czterech punktach
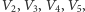 będących jednocześnie czterema brakującymi wierzchołkami pięciokąta foremnego.
będących jednocześnie czterema brakującymi wierzchołkami pięciokąta foremnego.
Wyprowadzimy teraz algebraicznie powyższą konstrukcję. Konstrukcja ta wykorzystuje podstawowe wiadomości dotyczące zbioru liczb zespolonych 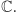
Liczby zespolone stanowią rozszerzenie liczb rzeczywistych o "pierwiastek z 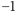 ". Formalnie liczby zespolone definiujemy jako zbiór par liczb rzeczywistych
". Formalnie liczby zespolone definiujemy jako zbiór par liczb rzeczywistych 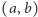 z działaniami dodawania oraz mnożenia zdefiniowanymi następująco:
z działaniami dodawania oraz mnożenia zdefiniowanymi następująco:

 oznacza się przez
oznacza się przez  Innym sposobem zapisu liczby zespolonej
Innym sposobem zapisu liczby zespolonej  jest jej postać algebraiczna
jest jej postać algebraiczna  Definiuje się część rzeczywistą
Definiuje się część rzeczywistą  oraz urojoną
oraz urojoną  ponadto definiuje się moduł liczby zespolonej
ponadto definiuje się moduł liczby zespolonej  oraz jej argument
oraz jej argument  będący wartością kąta nachylenia wektora
będący wartością kąta nachylenia wektora ![[a,b]](/math/temat/matematyka/algebra/2015/07/22/Okregi_Carlyle_a/12x-40ae973cb7ddd89ab8b70d3a271df72d8f79d212-im-33,33,33-FF,FF,FF.gif) na płaszczyźnie względem osi
na płaszczyźnie względem osi  Argument spełnia zależności
Argument spełnia zależności  oraz
oraz  Pozwala to na zapisanie liczby zespolonej w postaci trygonometrycznej
Pozwala to na zapisanie liczby zespolonej w postaci trygonometrycznej  oraz wykładniczej
oraz wykładniczej  która wynika ze wzoru Eulera
która wynika ze wzoru Eulera  prawdziwego dla dowolnej liczby rzeczywistej
prawdziwego dla dowolnej liczby rzeczywistej  Charakterystyczną cechą zbioru liczb zespolonych jest to, że wszystkie równania algebraiczne mają w nim pierwiastki. Równanie
Charakterystyczną cechą zbioru liczb zespolonych jest to, że wszystkie równania algebraiczne mają w nim pierwiastki. Równanie  nie ma rozwiązań rzeczywistych, natomiast ma dwa rozwiązania zespolone
nie ma rozwiązań rzeczywistych, natomiast ma dwa rozwiązania zespolone  oraz
oraz 
Przejdźmy do wyprowadzenia konstrukcji. Aby zbudować pięciokąt foremny, wystarczy skonstruować pierwiastki piątego stopnia z jedynki, czyli rozwiązać w zbiorze liczb zespolonych równanie
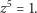 |
(4) |
Jednym z pierwiastków równania (4) jest, oczywiście, 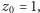 pozostałe natomiast spełniają równanie
pozostałe natomiast spełniają równanie
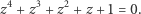 |
(5) |
Niech teraz 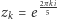 dla
dla 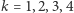 będą pierwiastkami równania (5). Zdefiniujmy
będą pierwiastkami równania (5). Zdefiniujmy
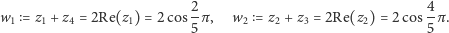 |
(6) |
Ze wzoru Viète'a na sumę pierwiastków wynika, że 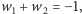 ponadto
ponadto

Ponownie korzystając ze wzorów Viète'a, stwierdzamy, że 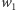 oraz
oraz 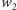 są pierwiastkami równania kwadratowego
są pierwiastkami równania kwadratowego 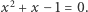 Konstruujemy zatem okrąg Carlyle'a o średnicy opartej na punktach
Konstruujemy zatem okrąg Carlyle'a o średnicy opartej na punktach 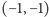 i
i 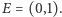 Jego środkiem jest punkt
Jego środkiem jest punkt 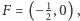 a punktami przecięcia z osią odciętych, zgodnie ze wzorem (6) są
a punktami przecięcia z osią odciętych, zgodnie ze wzorem (6) są 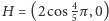 oraz
oraz 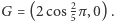 Symetralne odcinków
Symetralne odcinków 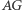 oraz
oraz 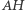 przecinają więc oś
przecinają więc oś 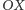 w punktach
w punktach 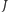 oraz
oraz 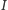 odpowiednio, których odcięte są równe częściom rzeczywistym odpowiednich pierwiastków. Ponieważ symetralne mają stałą odciętą, przecinają one okrąg każda w dwóch punktach, będących jednocześnie poszukiwanymi pierwiastkami równania (5).
odpowiednio, których odcięte są równe częściom rzeczywistym odpowiednich pierwiastków. Ponieważ symetralne mają stałą odciętą, przecinają one okrąg każda w dwóch punktach, będących jednocześnie poszukiwanymi pierwiastkami równania (5).
Wielokąty foremne mające 257 oraz 65537 boków również dają się skonstruować z wykorzystaniem okręgów Carlyle'a. Fizyczny model wymagałby jednak bardzo dokładnego oraz bardzo dużego cyrkla. O ile konstrukcja pięciokąta wymaga zaledwie jednego okręgu Carlyle'a, a konstrukcja siedemnastokąta czterech, to konstrukcja 257-kąta wymaga 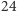 okręgów; jeden z nich jest rozwiązaniem równania
okręgów; jeden z nich jest rozwiązaniem równania  (a więc ma promień kilkadziesiąt razy większy niż okrąg jednostkowy, na którym budowany jest wielokąt). W przypadku 65537-kąta jeden z okręgów będzie stowarzyszony z równaniem
(a więc ma promień kilkadziesiąt razy większy niż okrąg jednostkowy, na którym budowany jest wielokąt). W przypadku 65537-kąta jeden z okręgów będzie stowarzyszony z równaniem 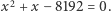 W 1991 roku stwierdzono, że liczba wymaganych w tym celu okręgów nie przekracza 1332 (!). Dokładna i wystarczająca ich liczba nie jest niestety znana autorowi artykułu.
W 1991 roku stwierdzono, że liczba wymaganych w tym celu okręgów nie przekracza 1332 (!). Dokładna i wystarczająca ich liczba nie jest niestety znana autorowi artykułu.