Logarytm – logika i rytm?
Dodawanie jest łatwe. Każdy się z tym zgodzi. Ot, zapisujemy dodawane liczby jedna pod drugą, dodajemy kolejne cyfry, bacząc na przeniesienia i to wszystko. Gorzej jest z mnożeniem...

Wyznaczenie iloczynu liczby  -cyfrowej przez liczbę
-cyfrowej przez liczbę 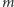 -cyfrową, gdzie
-cyfrową, gdzie 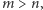 wymaga co najmniej dodania
wymaga co najmniej dodania 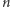 liczb o około
liczb o około 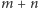 cyfrach każda. Zajmuje to dużo miejsca, czasu. Łatwo się pomylić. Zastanówmy się zatem, czy nie dałoby się jakoś tak "zakodować" liczb, aby zamiast mnożyć liczby jako takie, dodawać ich kody, a następnie wynik odkodować, dostając iloczyn. Innymi słowy, pytamy o istnienie funkcji
cyfrach każda. Zajmuje to dużo miejsca, czasu. Łatwo się pomylić. Zastanówmy się zatem, czy nie dałoby się jakoś tak "zakodować" liczb, aby zamiast mnożyć liczby jako takie, dodawać ich kody, a następnie wynik odkodować, dostając iloczyn. Innymi słowy, pytamy o istnienie funkcji  która spełnia związek:
która spełnia związek:
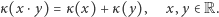 |
(*) |
No tak, ale już na pierwszy rzut oka widać, że jedyną taką funkcją jest funkcja stale równa zeru. Bo przecież  skąd
skąd 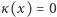 dla dowolnego
dla dowolnego 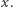
Hmm... To może złagodźmy nieco nasze wymagania? Właściwie po co mamy kodować zero? W końcu wszyscy wiedzą, jak się przez nie mnoży? Więcej - wystarczy takie kodowanie znaleźć tylko dla liczb dodatnich - przecież wiemy, jak znak iloczynu zależy od znaków czynników.
Tak więc szukamy funkcji 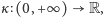 która spełnia związek
która spełnia związek 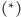 i która nie jest stale równa zeru. Więcej, szukać będziemy takiego
i która nie jest stale równa zeru. Więcej, szukać będziemy takiego  które jest ciągłe, czyli które dla bliskich wartości argumentów przyjmuje bliskie wartości i to w dodatku tak, aby dokładnością tego przybliżenia można było "sterować".
które jest ciągłe, czyli które dla bliskich wartości argumentów przyjmuje bliskie wartości i to w dodatku tak, aby dokładnością tego przybliżenia można było "sterować".
Wraz z warunkiem 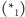 otrzymujemy, że
otrzymujemy, że 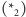 zachodzi dla
zachodzi dla 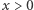 oraz
oraz  całkowitych. Dalej, jeśli
całkowitych. Dalej, jeśli 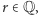 to
to 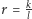 dla pewnych
dla pewnych 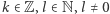 i wówczas
i wówczas

skąd 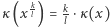 dla
dla 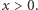 Czyli
Czyli 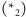 zachodzi dla
zachodzi dla 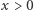 oraz
oraz  wymiernego. Ponieważ każdą liczbę niewymierną można z dowolną dokładnością przybliżać liczbami wymiernymi, postulowana wcześniej ciągłość funkcji
wymiernego. Ponieważ każdą liczbę niewymierną można z dowolną dokładnością przybliżać liczbami wymiernymi, postulowana wcześniej ciągłość funkcji 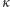 pozwala wywnioskować, że równość
pozwala wywnioskować, że równość 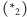 zachodzi dla dowolnej liczby rzeczywistej
zachodzi dla dowolnej liczby rzeczywistej 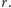
Z założeń, jakie nałożyliśmy na 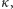 można łatwo wywnioskować, że
można łatwo wywnioskować, że 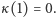 Zauważmy, że
Zauważmy, że 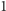 jest jedyną taką liczbą, dla której
jest jedyną taką liczbą, dla której  się zeruje. Przypuśćmy bowiem, że dla pewnego
się zeruje. Przypuśćmy bowiem, że dla pewnego  zachodzi
zachodzi 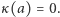 Niech dalej
Niech dalej  Ponieważ funkcja wykładnicza o podstawie
Ponieważ funkcja wykładnicza o podstawie 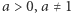 przyjmuje wszystkie dodatnie wartości, więc istnieje takie
przyjmuje wszystkie dodatnie wartości, więc istnieje takie 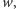 dla którego
dla którego  Stąd jednak
Stąd jednak 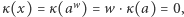 co przeczy założeniom o
co przeczy założeniom o 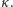
Udowodniona właśnie obserwacja implikuje w prosty sposób różnowartościowość funkcji 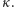 Załóżmy bowiem, że
Załóżmy bowiem, że  wówczas
wówczas 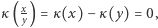 skąd właśnie
skąd właśnie 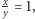 czyli
czyli 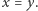 Co więcej, jedyność miejsca zerowego funkcji
Co więcej, jedyność miejsca zerowego funkcji  wraz z ciągłością tej ostatniej (a dokładniej z faktem, że ma ona własność Darboux) implikuje monotoniczność tej funkcji.
wraz z ciągłością tej ostatniej (a dokładniej z faktem, że ma ona własność Darboux) implikuje monotoniczność tej funkcji.
Niech bowiem 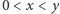 i
i 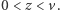 Wówczas dla
Wówczas dla 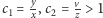 wartości
wartości 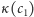 i
i 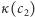 są tego samego znaku (inaczej jakieś
są tego samego znaku (inaczej jakieś  między
między 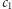 i
i 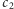 zerowałoby wartość
zerowałoby wartość 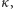 co nie jest możliwe). To zaś dowodzi, że bądź
co nie jest możliwe). To zaś dowodzi, że bądź  bądź
bądź 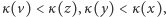 co wobec dowolności
co wobec dowolności 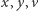 i
i  dowodzi monotoniczności
dowodzi monotoniczności 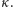
Założyliśmy, że 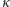 nie jest stale równa zeru, co oznacza, że istnieje
nie jest stale równa zeru, co oznacza, że istnieje 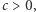 dla którego
dla którego 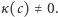 Ponieważ
Ponieważ 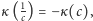 jedna z liczb
jedna z liczb 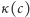 i
i 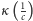 jest dodatnia, a druga ujemna. Oczywiście, możemy bez straty ogólności założyć, że to właśnie
jest dodatnia, a druga ujemna. Oczywiście, możemy bez straty ogólności założyć, że to właśnie 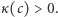 Teraz, skoro
Teraz, skoro 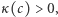 istnieją takie wymierne
istnieją takie wymierne  dla których
dla których 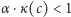 oraz
oraz 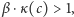 skąd
skąd 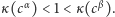 Ponieważ
Ponieważ 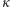 jest ciągła, spełnia ona własność Darboux, a stąd wynika, że istnieje taka wartość
jest ciągła, spełnia ona własność Darboux, a stąd wynika, że istnieje taka wartość 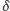 pomiędzy
pomiędzy 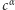 oraz
oraz  dla której
dla której  Zauważmy przy tym, że jeśli
Zauważmy przy tym, że jeśli 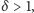 to
to  jest funkcją rosnącą, bo wówczas dla
jest funkcją rosnącą, bo wówczas dla 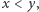 mamy
mamy 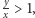 skąd wynika, że
skąd wynika, że 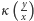 oraz
oraz 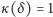 są tego samego znaku, czyli
są tego samego znaku, czyli 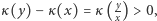 co oznacza, że
co oznacza, że 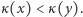
Teraz właściwie wszystko staje się jasne. Niech bowiem 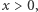 wówczas
wówczas

a stąd z różnowartościowości 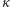 dostajemy
dostajemy 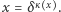
Innymi słowy, 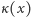 jest tą potęgą liczby
jest tą potęgą liczby 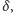 której wartością jest
której wartością jest 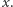 Taką liczbę nazywamy "logarytmem z
Taką liczbę nazywamy "logarytmem z 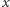 przy podstawie
przy podstawie 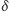 " i oznaczamy symbolem
" i oznaczamy symbolem 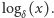 Ale przecież o tym wszyscy wiedzą - w końcu uczy się tego w szkołach...
Ale przecież o tym wszyscy wiedzą - w końcu uczy się tego w szkołach...
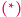
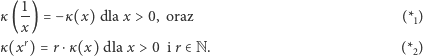
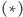 nie ma jednoznacznego rozwiązania. Dokładniej rzecz ujmując, istnieje nieprzeliczalnie wiele rozwiązań tego równania, wśród których dokładnie jedno jest ciągłe. Te nieciągłe są jednak bardzo paskudne.
nie ma jednoznacznego rozwiązania. Dokładniej rzecz ujmując, istnieje nieprzeliczalnie wiele rozwiązań tego równania, wśród których dokładnie jedno jest ciągłe. Te nieciągłe są jednak bardzo paskudne.