Schemat Falka
Wbrew często (i zazwyczaj bezmyślnie) powtarzanemu przysłowiu nie każdy obraz jest wart tysiąca słów. Ale niektóre są...
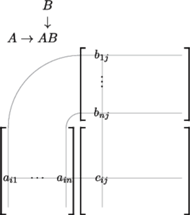
Rys. 1
Każdy student matematyki, informatyki lub politechniki na pierwszym roku
poznaje wzór, który definiuje iloczyn macierzy: jeśli liczba kolumn macierzy
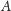 jest równa liczbie wierszy macierzy
jest równa liczbie wierszy macierzy
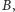 to ich iloczynem jest
macierz
to ich iloczynem jest
macierz
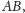 której współczynniki to
której współczynniki to
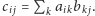 Takie
mnożenie macierzy jest znane od XIX wieku. Dopiero wiek później został
wynaleziony sposób jego zobrazowania, który dla mnie jest wart tysiąca słów,
a nawet trochę więcej.
Takie
mnożenie macierzy jest znane od XIX wieku. Dopiero wiek później został
wynaleziony sposób jego zobrazowania, który dla mnie jest wart tysiąca słów,
a nawet trochę więcej.
Schemat Falka, bo tak się ten wynalazek nazywa, składa się z tabelek ze
współczynnikami macierzy, rozmieszczonych jak na rysunku 1 Łatwo jest na
nim odnaleźć współczynniki macierzy
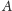 (na lewo) i
(na lewo) i
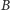 (powyżej), które mają wpływ na współczynnik
(powyżej), które mają wpływ na współczynnik
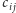 iloczynu. Wszystkie
znane własności mnożenia macierzy mają, oczywiście, dowody rachunkowe.
Schemat Falka pozwala zobaczyć wiele z tych własności, a to jest w pewnym
sensie coś więcej niż dowód.
iloczynu. Wszystkie
znane własności mnożenia macierzy mają, oczywiście, dowody rachunkowe.
Schemat Falka pozwala zobaczyć wiele z tych własności, a to jest w pewnym
sensie coś więcej niż dowód.
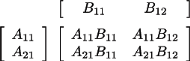
Rys. 2
Własność 1. Współczynniki nie muszą być liczbami, byleby można je było
jakoś mnożyć, a iloczyny jakoś dodawać; w tym sensie definicja iloczynu
macierzy jest uniwersalna. Na przykład (Rys. 2) współczynnikami mogą
być macierze (zwane blokami), jeśli tylko „pasują”, tj. dla każdego
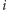 wszystkie bloki
wszystkie bloki
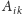 mają tyle samo wierszy, dla każdego
mają tyle samo wierszy, dla każdego
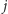 wszystkie bloki
wszystkie bloki
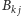 mają tyle samo kolumn, i dla każdego
mają tyle samo kolumn, i dla każdego
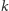 każdy blok
każdy blok
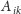 ma tyle samo kolumn, ile bloki
ma tyle samo kolumn, ile bloki
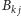 mają
wierszy. Jeśli bloki są macierzami liczbowymi, to mamy stąd ogólniejszy zapis
mnożenia macierzy liczbowych. Można też rozpatrywać bloki puste, tj.
mające 0 wierszy lub kolumn, co czasami jest wygodne.
mają
wierszy. Jeśli bloki są macierzami liczbowymi, to mamy stąd ogólniejszy zapis
mnożenia macierzy liczbowych. Można też rozpatrywać bloki puste, tj.
mające 0 wierszy lub kolumn, co czasami jest wygodne.
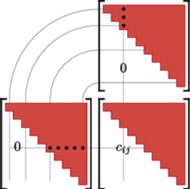
Rys. 3
Własność 2. O macierzy
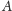 mówi się, że jest trójkątna górna, jeśli
wszystkie jej współczynniki
mówi się, że jest trójkątna górna, jeśli
wszystkie jej współczynniki
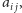 takie że
takie że
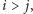 są równe
są równe
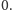 Mnożenie macierzy ma tę własność, że jeśli obie macierze
Mnożenie macierzy ma tę własność, że jeśli obie macierze
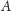 i
i
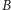 są trójkątne górne, to ich iloczyn też jest taki. Spójrzmy
na rysunek 3: po odnalezieniu współczynników w
są trójkątne górne, to ich iloczyn też jest taki. Spójrzmy
na rysunek 3: po odnalezieniu współczynników w
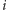 -tym wierszu
macierzy
-tym wierszu
macierzy
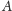 i
i
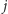 -tej kolumnie macierzy
-tej kolumnie macierzy
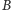 zauważamy, że
jeśli
zauważamy, że
jeśli
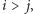 to w każdym iloczynie
to w każdym iloczynie
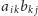 co najmniej jeden
czynnik jest zerem, a stąd
co najmniej jeden
czynnik jest zerem, a stąd
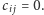 Analogiczna własność dotyczy
macierzy trójkątnych dolnych (takich że
Analogiczna własność dotyczy
macierzy trójkątnych dolnych (takich że
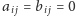 dla
dla
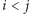 ), co
proponuję Czytelnikom narysować własnoręcznie.
), co
proponuję Czytelnikom narysować własnoręcznie.
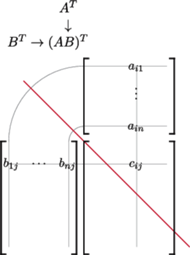
Rys. 4
Własność 3. Transpozycja przyporządkowuje dowolnej macierzy
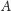 o współczynnikach
o współczynnikach
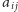 macierz
macierz
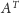 o współczynnikach
o współczynnikach
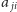 ; inaczej mówiąc, przekształcenie to zamienia wiersze z kolumnami.
Jeśli macierze
; inaczej mówiąc, przekształcenie to zamienia wiersze z kolumnami.
Jeśli macierze
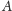 i
i
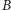 można pomnożyć (i mnożenie
współczynników jest przemienne), to
można pomnożyć (i mnożenie
współczynników jest przemienne), to
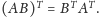 Ze schematu
Falka to wynika natychmiast po narysowaniu jego odbicia symetrycznego
względem ukośnej linii (tzw. diagonali macierzy
Ze schematu
Falka to wynika natychmiast po narysowaniu jego odbicia symetrycznego
względem ukośnej linii (tzw. diagonali macierzy
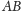 ), porównaj rysunki
1 i 4. Mnożenie macierzy (bloków) nie jest przemienne, dlatego dokonując
transpozycji iloczynu macierzy zbudowanych z bloków, tj. „odbijając”
schemat Falka, musimy „odbić”, czyli transponować każdy blok macierzy
), porównaj rysunki
1 i 4. Mnożenie macierzy (bloków) nie jest przemienne, dlatego dokonując
transpozycji iloczynu macierzy zbudowanych z bloków, tj. „odbijając”
schemat Falka, musimy „odbić”, czyli transponować każdy blok macierzy
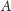 i
i
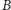 i ich iloczynu. Ale to po obejrzeniu rysunków jest
oczywiste.
i ich iloczynu. Ale to po obejrzeniu rysunków jest
oczywiste.
Własności 4 i 5. Macierz
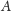 jest diagonalna, jeśli wszystkie współczynniki
oprócz
jest diagonalna, jeśli wszystkie współczynniki
oprócz
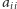 ma zerowe. Macierz permutacji jest to macierz kwadratowa,
która w każdym wierszu i w każdej kolumnie ma jeden współczynnik
równy
ma zerowe. Macierz permutacji jest to macierz kwadratowa,
która w każdym wierszu i w każdej kolumnie ma jeden współczynnik
równy
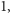 i pozostałe współczynniki
i pozostałe współczynniki
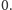 Wiersz
Wiersz
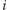 -ty
macierzy
-ty
macierzy
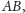 gdzie macierz
gdzie macierz
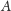 jest diagonalna, jest iloczynem
współczynnika
jest diagonalna, jest iloczynem
współczynnika
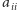 i
i
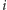 -tego wiersza macierzy
-tego wiersza macierzy
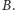 Jeśli zaś
Jeśli zaś
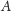 jest macierzą permutacji, to iloczyn
jest macierzą permutacji, to iloczyn
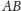 powstaje przez
poprzestawianie wierszy macierzy
powstaje przez
poprzestawianie wierszy macierzy
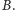 Narysowanie schematów (najlepiej
z użyciem bloków) i doprecyzowanie szczegółów polecam dla relaksu. A co
będzie, jeśli to drugi (tj. prawy) czynnik jest macierzą diagonalną lub
permutacji?
Narysowanie schematów (najlepiej
z użyciem bloków) i doprecyzowanie szczegółów polecam dla relaksu. A co
będzie, jeśli to drugi (tj. prawy) czynnik jest macierzą diagonalną lub
permutacji?
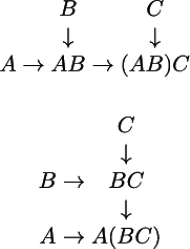
Rys. 5
Własność 6. Łączności mnożenia macierzy tak całkiem bez rachunków
pokazać się nie da, ale zobaczmy schematy na rysunku 5 Jest jasne, że wymiary
macierzy
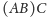 i
i
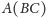 są identyczne. Jeśli w miejsce
są identyczne. Jeśli w miejsce
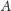 podstawimy blok
podstawimy blok
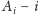 -ty wiersz macierzy
-ty wiersz macierzy
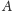 i zastąpimy
i zastąpimy
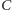 przez
przez
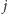 -tą kolumnę,
-tą kolumnę,
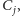 to w obu przypadkach
dostaniemy współczynnik na przecięciu
to w obu przypadkach
dostaniemy współczynnik na przecięciu
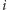 -tego wiersza i
-tego wiersza i
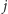 -tej
kolumny odpowiedniego iloczynu wszystkich trzech macierzy. Wyróżnimy
w macierzach bloki
-tej
kolumny odpowiedniego iloczynu wszystkich trzech macierzy. Wyróżnimy
w macierzach bloki
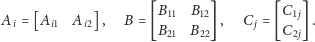 |
Podstawiając tak podzielone macierze do pierwszego schematu, dostaniemy
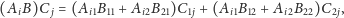 |
a z drugiego schematu otrzymamy
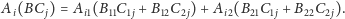 |
Jeśli mnożenie mniejszych bloków jest łączne i rozdzielne względem
dodawania, a dodawanie jest przemienne, to oba te wyrażenia mają tę samą
wartość. Ale to umożliwia przeprowadzenie dowodu indukcyjnego,
zaczynając od bloków pustych i bloków
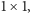 tj. zbudowanych
z pojedynczych współczynników.
tj. zbudowanych
z pojedynczych współczynników.
Schemat Falka z blokowym przedstawieniem macierzy został wykorzystany do
zilustrowania bardzo pięknego, równoległego algorytmu mnożenia dużych
macierzy przy użyciu karty graficznej w architekturze CUDA; zachęcam do
zapoznania się z nim w dokumentacji firmy NVIDIA. Tu zaś wykorzystamy
schemat Falka do przedstawienia idei szybkiego (sekwencyjnego) algorytmu
mnożenia wielkich macierzy rzadkich, czyli takich, których większość
współczynników (np. ponad
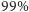 ) to zera. Iloczyn macierzy rzadkich
zwykle też jest macierzą rzadką, a przy tym każdy (lub prawie każdy) jego
niezerowy współczynnik jest sumą niewielu niezerowych składników.
Dopuszczamy zupełnie dowolne rozmieszczenie niezerowych współczynników
w macierzach
) to zera. Iloczyn macierzy rzadkich
zwykle też jest macierzą rzadką, a przy tym każdy (lub prawie każdy) jego
niezerowy współczynnik jest sumą niewielu niezerowych składników.
Dopuszczamy zupełnie dowolne rozmieszczenie niezerowych współczynników
w macierzach
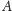 i
i
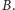 Chcielibyśmy, aby algorytm mnożył
i dodawał tylko liczby różne od zera.
Chcielibyśmy, aby algorytm mnożył
i dodawał tylko liczby różne od zera.
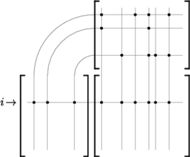
Rys. 6
Zobaczmy schemat na rysunku 6 W pokazanym przykładzie
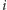 -ty wiersz
macierzy
-ty wiersz
macierzy
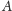 zawiera tylko trzy niezerowe współczynniki. Aby obliczyć
zawiera tylko trzy niezerowe współczynniki. Aby obliczyć
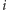 -ty wiersz iloczynu, trzeba pomnożyć przez nie odpowiednie trzy
wiersze macierzy
-ty wiersz iloczynu, trzeba pomnożyć przez nie odpowiednie trzy
wiersze macierzy
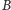 i dodać. Oczywiście, wystarczy odnaleźć
i pomnożyć tylko niezerowe współczynniki macierzy
i dodać. Oczywiście, wystarczy odnaleźć
i pomnożyć tylko niezerowe współczynniki macierzy
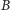 w tych
wierszach.
w tych
wierszach.
Obie macierze i ich iloczyn będziemy reprezentować za pomocą wykazów niezerowych współczynników. Wykaz jest tablicą, której każdy element zawiera indeksy wiersza i kolumny oraz niezerowy współczynnik na ich przecięciu.
Porządkiem wierszowym wykazu współczynników macierzy nazwiemy taką
kolejność jego elementów, że elementy reprezentujące niezerowe
współczynniki z każdego kolejnego wiersza są obok siebie (a w obrębie
wiersza elementy są uporządkowane dowolnie). W pierwszym kroku algorytmu
należy (np. za pomocą sortowania) uporządkować w ten sposób wykazy obu
macierzy,
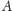 i
i
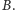 Następnie tworzymy dwie tablice pomocnicze,
których długości są o
Następnie tworzymy dwie tablice pomocnicze,
których długości są o
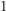 większe od liczb wierszy tych macierzy.
Kolejne elementy tablicy pomocniczej są indeksami uporządkowanego
wykazu, umożliwiającymi szybki dostęp do elementów reprezentujących
współczynniki każdego wiersza (liczba niezerowych współczynników
w wierszu jest różnicą dwóch kolejnych indeksów w pomocniczej tablicy, jej
ostatni element razem z przedostatnim umożliwia obliczenie liczby tych
współczynników w ostatnim wierszu).
większe od liczb wierszy tych macierzy.
Kolejne elementy tablicy pomocniczej są indeksami uporządkowanego
wykazu, umożliwiającymi szybki dostęp do elementów reprezentujących
współczynniki każdego wiersza (liczba niezerowych współczynników
w wierszu jest różnicą dwóch kolejnych indeksów w pomocniczej tablicy, jej
ostatni element razem z przedostatnim umożliwia obliczenie liczby tych
współczynników w ostatnim wierszu).

Aby obliczyć iloczyn
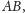 przeglądamy kolejne wiersze macierzy
przeglądamy kolejne wiersze macierzy
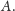 Dla współczynnika
Dla współczynnika
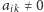 znajdujemy elementy reprezentujące
niezerowe współczynniki w
znajdujemy elementy reprezentujące
niezerowe współczynniki w
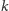 -tym wierszu macierzy
-tym wierszu macierzy
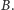 Dla
każdego takiego elementu, w dodatkowej tablicy, zapamiętujemy trójkę liczb:
indeks elementu reprezentującego współczynnik
Dla
każdego takiego elementu, w dodatkowej tablicy, zapamiętujemy trójkę liczb:
indeks elementu reprezentującego współczynnik
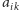 w wykazie
w wykazie
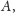 indeks elementu reprezentującego współczynnik
indeks elementu reprezentującego współczynnik
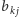 w wykazie
w wykazie
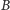 i indeks
i indeks
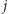 odpowiedniej kolumny macierzy
odpowiedniej kolumny macierzy
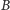 (czyli także iloczynu). Mając wszystkie takie trójki dla
(czyli także iloczynu). Mając wszystkie takie trójki dla
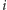 -tego
wiersza macierzy
-tego
wiersza macierzy
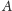 (i iloczynu), sortujemy ich ciąg względem
indeksów kolumn
(i iloczynu), sortujemy ich ciąg względem
indeksów kolumn
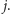 Po tym posortowaniu łatwo jest odnaleźć
odpowiednie współczynniki macierzy
Po tym posortowaniu łatwo jest odnaleźć
odpowiednie współczynniki macierzy
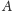 i
i
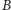 i wykonać
działania na nich, ponieważ iloczyny, których sumę trzeba obliczyć, są
reprezentowane przez trójki znajdujące się obok siebie. W ten sposób
otrzymamy niezerowe współczynniki w
i wykonać
działania na nich, ponieważ iloczyny, których sumę trzeba obliczyć, są
reprezentowane przez trójki znajdujące się obok siebie. W ten sposób
otrzymamy niezerowe współczynniki w
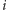 -tym wierszu macierzy
-tym wierszu macierzy
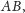 a ściślej te współczynniki, które są sumami niezerowych
składników.
a ściślej te współczynniki, które są sumami niezerowych
składników.
Koszt tego algorytmu w istotny sposób zależy od użytego algorytmu sortowania, ale są znane bardzo szybkie algorytmy sortowania, których użycie sprawia, że obliczenia pomocnicze zabierają tylko kilka razy więcej czasu niż same działania na współczynnikach. Można też opracować podobny algorytm, korzystający z kolumnowego uporządkowania wykazów.
Rysunkowe przedstawienie mnożenia macierzy wymyślił w latach 50. dwudziestego wieku Sigurd Falk, profesor politechniki w Brunszwiku. Opisane wyżej przykłady nie wyczerpują zastosowań tego wynalazku, ale mam nadzieję, że uzasadniają jego wartość, przy użyciu kilku obrazków i w przybliżeniu 1100 słów.