Pojedynek, symetrie i potwór – klasyfikacja grup prostych

Évariste Galois
30 maja 1832 roku w Paryżu zginął w pojedynku młody matematyk, Evariste Galois. Nie ma pewności, czy pojedynek ten miał podłoże polityczne, czy też Galois bronił honoru pewnej młodej damy. W pożegnalnym liście poprosił on, by jego notatki wysłać Jacobiemu albo Gaussowi. Żaden z tych wielkich matematyków nigdy nie zobaczył jednak zapisków Galois.
Czternaście lat później inny znany matematyk, Liouville, opublikował wyniki Galois razem z komentarzami. Co jednak było w nich aż tak interesującego? Galois zajmował się problemem istnienia wzorów na pierwiastki równań danych przez wielomiany. Większość Czytelników zna wzór na pierwiastki równania drugiego stopnia, słynne be kwadrat minus cztery a ce, a nieliczni słyszeli również o wzorach Cardano na rozwiązania równania stopnia trzeciego, czy Ferrariego, które stosujemy przy równaniach stopnia czwartego. Czy można w podobny sposób opisać rozwiązania dowolnego równania stopnia piątego?
Galois zauważył, że mimo iż na mocy Zasadniczego Twierdzenia Algebry równanie piątego stopnia ma aż pięć pierwiastków, to pierwiastki te nie są całkowicie niezależne – tworzą one grupy, a w każdej takiej grupie można zaobserwować pewne zależności, symetrie między pierwiastkami. Geniusz Galois polegał na tym, że skupił się on na tych symetriach, a nie na samych pierwiastkach.
Zmianę kolejności elementów w zbiorze nazywamy permutacją. Galois zainteresował fakt, że jeśli użyjemy najpierw jednej permutacji, a potem drugiej, to możemy tej parze przypisać trzecią permutację, która da ten sam efekt. Galois nazwał taki system łączenia permutacji grupą permutacji. Kluczowym pomysłem jego pracy było rozkładanie grup permutacji na prostsze grupy, które współczesny matematyk, Mark Ronan (Symmetry and the Monster, Oxford University Press, 2006), nazywa atomami symetrii. Nazwa ta jest trafna – atom pochodzi od greckiego niepodzielny, więc to określenie pasuje do grup, których na prostsze rozłożyć się nie da. Mniej romantyczna nazwa tych atomów to grupy proste.
Powiemy, że zbiór permutacji
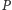 generuje grupę
generuje grupę
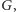 jeśli
dowolną permutację z
jeśli
dowolną permutację z
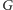 możemy przedstawić jako złożenie potęg
elementów zbioru
możemy przedstawić jako złożenie potęg
elementów zbioru
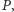 gdzie potęga permutacji
gdzie potęga permutacji
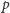 to jej wielokrotne
złożenie. Grupa
to jej wielokrotne
złożenie. Grupa
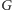 jest cykliczna, jeśli generuje ją jeden element.
Rzędem grupy
jest cykliczna, jeśli generuje ją jeden element.
Rzędem grupy
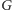 nazywamy liczbę jej elementów, zaś rząd elementu
nazywamy liczbę jej elementów, zaś rząd elementu
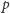 to moc grupy generowanej przez ten element. Pierwsze atomy symetrii,
jakie udało się znaleźć, to grupy cykliczne o rzędach będących liczbami
pierwszymi. Jakie są inne atomy? Czy możemy te atomy w jakiś sposób
sklasyfikować?
to moc grupy generowanej przez ten element. Pierwsze atomy symetrii,
jakie udało się znaleźć, to grupy cykliczne o rzędach będących liczbami
pierwszymi. Jakie są inne atomy? Czy możemy te atomy w jakiś sposób
sklasyfikować?
Grupy Liego, które powstały w związku z jego badaniami nad równaniami różniczkowymi, oraz pomysł Killinga na układ okresowy tych grup nadały kierunek poszukiwaniom. Udało się sklasyfikować istniejące atomy, umieszczając je w odpowiednich rodzinach. Okazało się jednak, że na tym nie koniec.
Puszka Pandory
W opowiadaniu Uncle Petros and Goldbach’s Conjecture autorstwa Apostolosa Doxiadisa pojawia się matematyk, który przez całą swoją karierę próbuje rozwiązać pewien stary problem. Mianowicie, czy każdą parzystą liczbę większą od 2 możemy przedstawić jako sumę dwóch liczb pierwszych? Jest to jedno z pytań, na które do tej pory nie udało się znaleźć odpowiedzi, chociaż poszukiwania trwają od dawna. Co sprawia, że niektóre problemy matematyczne są tak ciężkie do rozwiązania? Czy, tak jak w tym przypadku, trudność polega na tym, że nie wiemy, jak się do tego zabrać, czy może po prostu droga do rozwiązania jest długa i stroma?
Do tej drugiej grupy problemów zdecydowanie należy zaliczyć (przynajmniej dziś) twierdzenie Feita-Thompsona o nieparzystym rzędzie. Jego sformułowanie jest bardzo proste:
Jeśli atom symetrii nie jest cykliczną grupą o rzędzie będącym liczbą pierwszą, to jego rząd jest parzysty.
Dowód miał jednak 255 stron i zajął cały numer Pacific Journal of Mathematics. Dlaczego jednak twierdzenie to było tak ważne przy poszukiwaniu atomów symetrii?
Cauchy udowodnił, że jeśli rząd grupy dzieli się przez liczbę pierwszą
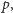 to w grupie tej istnieje element rzędu
to w grupie tej istnieje element rzędu
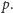 Jeśli więc rząd atomu
symetrii jest liczbą parzystą, to atom ten musi zawierać element rzędu
Jeśli więc rząd atomu
symetrii jest liczbą parzystą, to atom ten musi zawierać element rzędu
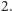 Taki element (a dokładniej mnożenie przez niego) zachowuje się
podobnie jak symetria lustrzana. Jeśli odbijemy przedmiot raz, to znajdzie się on
po drugiej stronie lustra, a jeśli odbijemy go ponownie, to wróci na swoje
miejsce. Składając tę symetrię z innymi, możemy otrzymać symetrię względem
innego lustra. Znajdą się jednak takie symetrie, które utrzymają lustro w tym
samym miejscu. Podgrupę permutacji niezmieniających wybranego lustra
będziemy nazywać przekrojem poprzecznym. Do czego potrzebny jest nam
jednak taki twór?
Taki element (a dokładniej mnożenie przez niego) zachowuje się
podobnie jak symetria lustrzana. Jeśli odbijemy przedmiot raz, to znajdzie się on
po drugiej stronie lustra, a jeśli odbijemy go ponownie, to wróci na swoje
miejsce. Składając tę symetrię z innymi, możemy otrzymać symetrię względem
innego lustra. Znajdą się jednak takie symetrie, które utrzymają lustro w tym
samym miejscu. Podgrupę permutacji niezmieniających wybranego lustra
będziemy nazywać przekrojem poprzecznym. Do czego potrzebny jest nam
jednak taki twór?
Pomysł jest prosty. Zamiast szukać atomów symetrii, spróbujmy zrozumieć ich przekroje poprzeczne. Zacznijmy od przekrojów znanych nam atomów i pokażmy, że nie mogą istnieć inne, mające te same przekroje. Okazało się jednak, że to nie takie proste.
Nowe atomy
W połowie XIX wieku, kiedy opublikowane zostały prace Galois, wielu
matematyków zainteresowało się teorią grup, a w szczególności grupami
permutacji. Powstało wtedy pojęcie tranzytywnej (przechodniej) grupy
permutacji. Grupa ta, działając na zbiorze obiektów, spełniała warunek, że
dowolnie wybrany obiekt możemy zamienić miejscami z dowolnym innym
obiektem. W podobny sposób możemy zdefiniować grupy wielokrotnie
przechodnie. Grupa
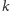 -przechodnia to taka, która dla dwóch dowolnych
podzbiorów złożonych z
-przechodnia to taka, która dla dwóch dowolnych
podzbiorów złożonych z
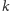 obiektów zawiera przekształcenie, które
zamienia miejscami odpowiednie pary tych obiektów. Badając grupy
obiektów zawiera przekształcenie, które
zamienia miejscami odpowiednie pary tych obiektów. Badając grupy
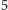 -przechodnie, francuski matematyk Mathieu wpadł na ślad dwóch
nowych atomów, które oznaczył odpowiednio
-przechodnie, francuski matematyk Mathieu wpadł na ślad dwóch
nowych atomów, które oznaczył odpowiednio
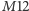 i
i
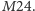 Nie
udało mu się jednak udowodnić istnienia tych grup. W końcu, ponad
Nie
udało mu się jednak udowodnić istnienia tych grup. W końcu, ponad
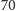 lat później, na seminarium w Hamburgu, niemiecki matematyk
Ernst Witt zdefiniował
lat później, na seminarium w Hamburgu, niemiecki matematyk
Ernst Witt zdefiniował
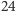 symbole, których grupa symetrii to właśnie
symbole, których grupa symetrii to właśnie
Interesujące jest, że atomy Mathieu nie należą do żadnej ze znanych rodzin atomów. Skoro jednak znaleźliśmy kilka samotnych atomów (takie samotne atomy zostały nazwane grupami sporadycznymi), to czy może być ich więcej?
Odpowiedź brzmi: tak. Korzystając z opisanych wcześniej przekrojów
poprzecznych, matematycy Janko i Thompson odnaleźli grupy, nazwane na
cześć Janko
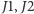 i
i
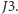
Radio i sieci
Pierwsze odkryte grupy sporadyczne miały nadspodziewanie dużo elementów. Na przykład, najmniej liczna spośród grup odkrytych przez Mathieu miała ich 7920. Powstało pytanie, jakie to obiekty mogą mieć tak liczne i nietypowe grupy symetrii.
Inspiracja przyszła od strony radia. W czasach pierwszych transmisji radiowych często zdarzało się, że dźwięki zakłócane były przez szumy, mimo że stacje radiowe starały się zachowywać jak najwyższą jakość transmisji. Szukając rozwiązania problemu, Claude Shannon z Bell Labs zaproponował, by sygnał radiowy wysyłany był jako seria krótkich dźwięków kodujących informację w taki sposób, żeby niewielkie zakłócenia mogły być natychmiast poprawiane, co zwiększyłoby jakość przekazu.
Dogodnym modelem takich sytuacji są gęsto upakowane sieci o ustalonej odległości między węzłami, na dodatek w wielowymiarowej przestrzeni.
Badając przestrzeń o wymiarze równym
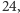 matematyk John Leech
zdefiniował nową sieć tego typu (nazywaną kratą Leecha). Doszedł on
również do wniosku, że jest to struktura na tyle ciekawa, że warto
sprawdzić, co kryje grupa jej symetrii. Udało mu się przekonać innego
matematyka, Johna Conwaya, by zajął się badaniem możliwości otrzymania
z niej kolejnych atomów symetrii, co doprowadziło Conwaya do uzyskania
trzech nowych atomów
matematyk John Leech
zdefiniował nową sieć tego typu (nazywaną kratą Leecha). Doszedł on
również do wniosku, że jest to struktura na tyle ciekawa, że warto
sprawdzić, co kryje grupa jej symetrii. Udało mu się przekonać innego
matematyka, Johna Conwaya, by zajął się badaniem możliwości otrzymania
z niej kolejnych atomów symetrii, co doprowadziło Conwaya do uzyskania
trzech nowych atomów
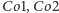 i
i
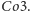
Potwór Fischera

Matematyk Bernd Fischer postanowił zająć się problemem, którego
sformułowanie było proste: jakie grupy permutacji, generowane przez permutacje
rzędu
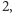 zachowują się podobnie jak transpozycje? Transpozycja to
permutacja, która zamienia miejscami dwa ustalone elementy. Łatwo jest
wykazać, że złożenie dwóch transpozycji ma albo rząd
zachowują się podobnie jak transpozycje? Transpozycja to
permutacja, która zamienia miejscami dwa ustalone elementy. Łatwo jest
wykazać, że złożenie dwóch transpozycji ma albo rząd
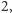 albo
rząd
albo
rząd
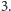 Te permutacje, tak zbliżone do transpozycji, nazywamy
transpozycjami Fischera. Fischerowi udało się udowodnić następujące
twierdzenie:
Te permutacje, tak zbliżone do transpozycji, nazywamy
transpozycjami Fischera. Fischerowi udało się udowodnić następujące
twierdzenie:
Jeśli atom symetrii (albo coś bardzo do niego podobnego) jest generowany
przez transpozycje Fischera, to może on być tylko jednym z
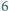 typów
obiektów.
typów
obiektów.
Analizując te typy obiektów, Fischer uzyskał trzy nowe interesujące grupy, blisko
związane z grupami Mathieu
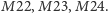 Oznaczył je jako
Oznaczył je jako
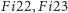 i
i
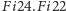 i
i
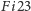 są atomami, zaś
są atomami, zaś
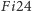 zawiera olbrzymi atom rozmiaru
zawiera olbrzymi atom rozmiaru
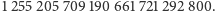
Możemy porównać transpozycje Fischera do luster, które odbijają część
obiektów, a resztę pozostawiają niezmienioną. Jeśli ustawimy dwa lustra pod
kątem
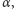 to złożenie odbić w tych lustrach będzie obrotem o kąt
to złożenie odbić w tych lustrach będzie obrotem o kąt
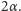 Jeśli rząd złożenia dwóch symetrii lustrzanych ma być równy
Jeśli rząd złożenia dwóch symetrii lustrzanych ma być równy
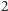 lub
lub
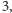 to kąty pomiędzy lustrami mogą być tylko równe
to kąty pomiędzy lustrami mogą być tylko równe
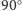 lub
lub
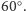 Rozważając pewne specyficzne zbiory tych
luster, czyli układy generatorów, Fischer udowodnił podane wcześniej
twierdzenie.
Rozważając pewne specyficzne zbiory tych
luster, czyli układy generatorów, Fischer udowodnił podane wcześniej
twierdzenie.
Następny krok można przedstawić jako dopuszczenie ustawienia luster pod
kątem
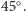 To doprowadziło Fischera do większego atomu, który zdawał
się zawierać
To doprowadziło Fischera do większego atomu, który zdawał
się zawierać
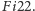 Dzięki temu udało mu się stworzyć nowy
atom symetrii, który nazwał
Dzięki temu udało mu się stworzyć nowy
atom symetrii, który nazwał
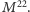 Dodatkowo zauważył, że
Dodatkowo zauważył, że
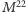 może być przekrojem poprzecznym innego atomu symetrii, który
z powodu powiązań z
może być przekrojem poprzecznym innego atomu symetrii, który
z powodu powiązań z
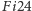 został oznaczony jako
został oznaczony jako
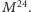 Istniało
podejrzenie, że pomiędzy
Istniało
podejrzenie, że pomiędzy
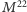 a
a
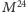 ukrywa się trzecia grupa,
więc Conway, z którym Fischer podzielił się swoimi spostrzeżeniami, nazwał te
trzy grupy odpowiednio Małym Potworem, Średnim Potworem i Super
Potworem. Gdy później okazało się, że Średni Potwór nie może istnieć,
nazwy zmieniono na Mały Potwór i Potwór.
ukrywa się trzecia grupa,
więc Conway, z którym Fischer podzielił się swoimi spostrzeżeniami, nazwał te
trzy grupy odpowiednio Małym Potworem, Średnim Potworem i Super
Potworem. Gdy później okazało się, że Średni Potwór nie może istnieć,
nazwy zmieniono na Mały Potwór i Potwór.
Potwór okazał się być grupą, której rząd wynosi

Naukowcom z Cambridge udało się udowodnić, że Potwór nietrywialnie
działa na przestrzeni o wymiarze
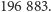 Najoszczędniejsza forma,
w jakiej udało się zawrzeć pełne informacje o tej grupie, ma postać tabeli
o 194 wierszach i tyluż kolumnach. Aby ją wypełnić (obliczyć), potrzeba
było roku pracy, w którą zaangażowano wszystkie (ówczesne) komputery
uniwersytetu w Birmingham.
Najoszczędniejsza forma,
w jakiej udało się zawrzeć pełne informacje o tej grupie, ma postać tabeli
o 194 wierszach i tyluż kolumnach. Aby ją wypełnić (obliczyć), potrzeba
było roku pracy, w którą zaangażowano wszystkie (ówczesne) komputery
uniwersytetu w Birmingham.
Jako że dwie podgrupy Potwora również okazały się atomami symetrii, to
w sumie udało się odnaleźć 25 atomów niezrzeszonych w znanych
wcześniej rodzinach. W 1975 roku Janko udowodnił istnienie jeszcze
jednego atomu,
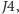 który wkrótce został dokładniej opisany.
Od tego czasu liczba tych ważnych grup już się nie zmieniła i się nie
zmieni.
który wkrótce został dokładniej opisany.
Od tego czasu liczba tych ważnych grup już się nie zmieniła i się nie
zmieni.