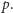Hipoteza Kakeyi
Wyobraźmy sobie igłę umieszczoną wewnątrz pewnego zbioru na płaszczyźnie.
Igłę traktujemy jak odcinek jednostkowy, który możemy dowolnie obracać
i przesuwać w obrębie naszego zbioru. Załóżmy, że chcielibyśmy
wykonać igłą obrót o
 – jak wiele miejsca do tego potrzeba?
– jak wiele miejsca do tego potrzeba?

Oczywiście, możemy umieścić igłę na środku koła o promieniu
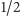 i obrócić ją bez przesuwania, co wymaga pola równego
i obrócić ją bez przesuwania, co wymaga pola równego
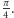 Po chwili zastanowienia widać, że rozwiązanie to nie jest optymalne.
Umieszczając igłę wewnątrz kształtu utworzonego przez trzy łuki deltoidy,
przedstawionego na rysunku, a następnie przesuwając i obracając ją tak,
aby w każdej chwili stykała się z brzegiem figury w trzech punktach,
możemy wykonać pełny obrót przy polu
Po chwili zastanowienia widać, że rozwiązanie to nie jest optymalne.
Umieszczając igłę wewnątrz kształtu utworzonego przez trzy łuki deltoidy,
przedstawionego na rysunku, a następnie przesuwając i obracając ją tak,
aby w każdej chwili stykała się z brzegiem figury w trzech punktach,
możemy wykonać pełny obrót przy polu
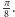 Czy da się jeszcze
lepiej?
Czy da się jeszcze
lepiej?
Pytanie to zadał po raz pierwszy japoński matematyk Soichi Kakeya w 1917 roku. Jak łatwo się przekonać, aby wewnątrz zbioru dało się wykonać pełny obrót igły, musi on zawierać odcinek jednostkowy w każdym kierunku. Własność ta ma sens nie tylko na płaszczyźnie, ale też w przestrzeni dowolnego wymiaru, co motywuje następującą definicję:
Zaskakującej odpowiedzi na pytanie Kakeyi udzielił Abraham Besicovitch w 1919 roku. Okazuje się, że istnieją zbiory o dowolnie małym polu, wewnątrz których można obrócić igłę! Co więcej, można nawet skonstruować zbiory Kakeyi o polu równym zeru. Konstrukcję, opartą o sprytne sklejanie trójkątów o coraz mniejszych polach, można obejrzeć na stronie http://www.math.ucla.edu/ tao/java/Besicovitch.html.
To jednak jeszcze nie koniec. Nawet wśród zbiorów o mierze zero istnieją zbiory „mniejsze” i „większe”. Intuicję z tym związaną formalnie ujmuje pojęcie tzw. wymiaru Minkowskiego, który (mówiąc bardzo ogólnie) mierzy, jak dobrze zbiór wypełnia przestrzeń. Wymiar ten może być liczbą niecałkowitą.
Przykładami zbiorów o niecałkowitym wymiarze Minkowskiego są
zbiory samopodobne (fraktale). Maksymalny możliwy wymiar zbioru
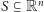 wynosi
wynosi

Możemy teraz wrócić do pytania, jak duży w sensie wymiaru Minkowskiego musi być zbiór Kakeyi.
Hipoteza (Hipoteza Kakeyi). Jeśli
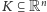 jest
zbiorem Kakeyi w przestrzeni
jest
zbiorem Kakeyi w przestrzeni
 -wymiarowej, to
-wymiarowej, to
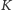 ma wymiar
Minkowskiego (i wymiar Hausdorffa) równy
ma wymiar
Minkowskiego (i wymiar Hausdorffa) równy
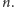
Hipotezę tę udało się dotychczas udowodnić jedynie dla
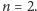 W wyższych
wymiarach, pomimo wysiłków wielu matematyków, pozostaje ona
problemem otwartym, powiązanym z wieloma działami matematyki,
między innymi z analizą harmoniczną i równaniami różniczkowymi
cząstkowymi.
W wyższych
wymiarach, pomimo wysiłków wielu matematyków, pozostaje ona
problemem otwartym, powiązanym z wieloma działami matematyki,
między innymi z analizą harmoniczną i równaniami różniczkowymi
cząstkowymi.
Skoro nie potrafimy udowodnić hipotezy Kakeyi w
 nasuwa się
pytanie, czy istnieje jakaś prostsza wersja lub szczególny przypadek problemu,
który łatwiej rozwiązać. Zwróćmy uwagę, że do zdefiniowania zbioru
Kakeyi potrzebujemy jedynie abstrakcyjnego pojęcia prostej czy odcinka,
natomiast nie jest istotne, że mamy do czynienia z liczbami rzeczywistymi.
W szczególności możemy rozważać dyskretny wariant problemu,
w którym
nasuwa się
pytanie, czy istnieje jakaś prostsza wersja lub szczególny przypadek problemu,
który łatwiej rozwiązać. Zwróćmy uwagę, że do zdefiniowania zbioru
Kakeyi potrzebujemy jedynie abstrakcyjnego pojęcia prostej czy odcinka,
natomiast nie jest istotne, że mamy do czynienia z liczbami rzeczywistymi.
W szczególności możemy rozważać dyskretny wariant problemu,
w którym
 -wymiarową przestrzeń euklidesową zastępujemy
przestrzenią nad ciałem skończonym.
-wymiarową przestrzeń euklidesową zastępujemy
przestrzenią nad ciałem skończonym.
Niech
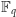 będzie ciałem o
będzie ciałem o
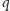 elementach. Przez
elementach. Przez
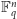 będziemy oznaczać zbiór wektorów
będziemy oznaczać zbiór wektorów
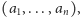 gdzie
gdzie
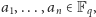 z naturalną operacją dodawania po współrzędnych. Zamiast
przestrzeni euklidesowej
z naturalną operacją dodawania po współrzędnych. Zamiast
przestrzeni euklidesowej
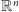 rozważamy więc skończoną przestrzeń
rozważamy więc skończoną przestrzeń
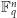 o
o
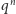 elementach. Prostą w kierunku
elementach. Prostą w kierunku
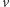 przechodzącą
przez punkt
przechodzącą
przez punkt
 gdzie
gdzie
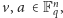 nazwiemy, podobnie jak
w przypadku euklidesowym, zbiór postaci
nazwiemy, podobnie jak
w przypadku euklidesowym, zbiór postaci
 Każda taka
prosta zawiera
Każda taka
prosta zawiera
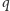 punktów.
punktów.
Ponieważ nasza przestrzeń jest teraz skończona, bardziej naturalne w definicji zbioru Kakeyi będzie zastąpienie odcinków prostymi.
Aby sformułować hipotezę Kakeyi dla ciał skończonych, potrzebujemy jeszcze
dyskretnego odpowiednika wymiaru. W przestrzeni
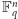 naturalnym
odpowiednikiem zbioru wymiaru
naturalnym
odpowiednikiem zbioru wymiaru
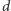 będzie zbiór mocy rzędu
będzie zbiór mocy rzędu
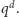 Prowadzi to do następującej hipotezy.
Prowadzi to do następującej hipotezy.
Twierdzenie 1 (Hipoteza Kakeyi dla ciał skończonych). Niech
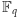 będzie ciałem skończonym o
będzie ciałem skończonym o
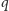 elementach. Dla każdego
elementach. Dla każdego
 istnieje taka stała
istnieje taka stała
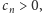 niezależna od
niezależna od
 że
jeśli
że
jeśli
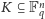 jest zbiorem Kakeyi, to
jest zbiorem Kakeyi, to

Problem ma teraz bardziej kombinatoryczny charakter niż w przypadku euklidesowym, co nie znaczy, że musi być łatwiejszy do rozwiązania. Hipotezę Kakeyi dla ciał skończonych postawiono w 1999 roku. Przez dziesięć lat, pomimo prób wielu matematyków, w tym medalistów Fieldsa, nie udało się jednak jej udowodnić.
W związku z tym wielkim zaskoczeniem okazał się przedstawiony przez Zeeva Dvira w 2009 roku piękny i prosty dowód hipotezy Kakeyi dla ciał skończonych. Dowód, z pewnością zasługujący na miano Dowodu z Księgi, korzysta z tzw. metody wielomianowej, stosowanej już wcześniej w kombinatoryce, a przy tym jest tak elementarny, że daje się zrozumieć z wykorzystaniem podstawowej wiedzy licealnej!
W dowodzie kluczową rolę grają wielomiany nad ciałami skończonymi. Niech
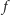 będzie wielomianem
będzie wielomianem
 zmiennych
zmiennych
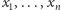 o współczynnikach
z
o współczynnikach
z
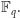 Powiemy, że
Powiemy, że
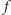 ma miejsce zerowe w punkcie
ma miejsce zerowe w punkcie
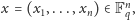 jeśli
jeśli
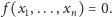 Stopniem
jednomianu postaci
Stopniem
jednomianu postaci
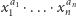 nazywamy sumę wykładników:
nazywamy sumę wykładników:
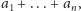 a stopniem wielomianu – największy stopień jednomianu
wchodzącego w skład
a stopniem wielomianu – największy stopień jednomianu
wchodzącego w skład
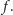

Przed przystąpieniem do dowodu hipotezy przedstawiamy dwa lematy, których
dowód jest ćwiczeniem dla Czytelnika. Nad ciałem nieskończonym (np.
 ) wielomian zerujący się w każdym punkcie ciała musi być
tożsamościowo równy zeru (mieć wszystkie współczynniki zerowe).
Zauważmy, że nie jest to prawda nad ciałami skończonymi – dla dowolnego
ciała skończonego
) wielomian zerujący się w każdym punkcie ciała musi być
tożsamościowo równy zeru (mieć wszystkie współczynniki zerowe).
Zauważmy, że nie jest to prawda nad ciałami skończonymi – dla dowolnego
ciała skończonego
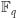 wielomian
wielomian
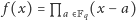 jest
wielomianem stopnia
jest
wielomianem stopnia
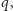 który zeruje się w każdym punkcie
który zeruje się w każdym punkcie
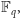 a nie jest tożsamościowo równy zeru. Każdy wielomian o tej
własności musi mieć jednak odpowiednio wysoki stopień, o czym mówi
następujący lemat.
a nie jest tożsamościowo równy zeru. Każdy wielomian o tej
własności musi mieć jednak odpowiednio wysoki stopień, o czym mówi
następujący lemat.
Lemat 1 (Lemat Schwartza–Zippela). Niech
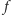 będzie wielomianem
będzie wielomianem
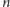 zmiennych
zmiennych
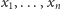 o współczynnikach
z
o współczynnikach
z
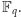 Niech
Niech
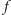 ma stopień
ma stopień
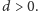 Wtedy liczba miejsc
zerowych
Wtedy liczba miejsc
zerowych
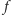 wynosi co najwyżej
wynosi co najwyżej
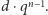
Dowód przebiega przez indukcję względem
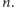 Dla
Dla
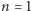 jest to
po prostu stwierdzenie, że wielomian jednej zmiennej, mający stopień
jest to
po prostu stwierdzenie, że wielomian jednej zmiennej, mający stopień
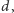 ma co najwyżej
ma co najwyżej
 miejsc zerowych. W szczególności, jeśli
wielomian
miejsc zerowych. W szczególności, jeśli
wielomian
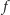 ma stopień nie większy niż
ma stopień nie większy niż
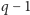 i zeruje się
w każdym punkcie
i zeruje się
w każdym punkcie
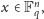 to musi być tożsamościowo równy
zeru.
to musi być tożsamościowo równy
zeru.
Lemat 2. Niech
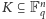 będzie zbiorem mocy mniejszej niż
będzie zbiorem mocy mniejszej niż
 Wtedy
istnieje wielomian
Wtedy
istnieje wielomian
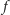 w zmiennych
w zmiennych
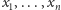 stopnia co
najwyżej
stopnia co
najwyżej
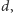 który zeruje się we wszystkich punktach
który zeruje się we wszystkich punktach
 i nie
jest tożsamościowo równy zeru.
i nie
jest tożsamościowo równy zeru.
W dowodzie kluczowa jest obserwacja, że jednomianów w zmiennych
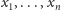 stopnia co najwyżej
stopnia co najwyżej
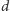 jest dokładnie
jest dokładnie
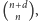 wobec
czego układ równań na współczynniki wielomianu
wobec
czego układ równań na współczynniki wielomianu
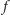 o zadanych
właściwościach ma niezerowe rozwiązania.
o zadanych
właściwościach ma niezerowe rozwiązania.
Mając w ręku powyższe lematy, możemy przystąpić do dowodu hipotezy
Kakeyi. Przypuśćmy, że istnieje zbiór Kakeyi
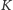 o mniej niż
o mniej niż
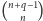 elementach. Z Lematu 2 wnioskujemy, że istnieje nietrywialny
wielomian
elementach. Z Lematu 2 wnioskujemy, że istnieje nietrywialny
wielomian
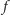 stopnia co najwyżej
stopnia co najwyżej
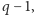 zerujący się w każdym
punkcie
zerujący się w każdym
punkcie
 Zbiór
Zbiór
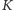 jest zbiorem Kakeyi, więc dla dowolnego
niezerowego wektora
jest zbiorem Kakeyi, więc dla dowolnego
niezerowego wektora
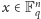 zawiera on prostą w kierunku
zawiera on prostą w kierunku
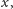 czyli
zbiór postaci
czyli
zbiór postaci
 dla pewnego
dla pewnego
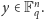 Rozpatrzmy
teraz obcięcie wielomianu
Rozpatrzmy
teraz obcięcie wielomianu
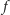 do prostej w kierunku
do prostej w kierunku
 a więc
wielomian jednej zmiennej
a więc
wielomian jednej zmiennej
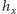 określony jako
określony jako
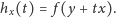
Dla każdego
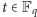 mamy
mamy
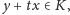 więc
więc
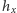 zeruje się
punkcie
zeruje się
punkcie
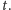 Oznacza to, że
Oznacza to, że
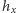 zeruje się w każdym punkcie
ciała
zeruje się w każdym punkcie
ciała
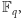 a ponieważ (tak jak
a ponieważ (tak jak
 ) ma stopień co najwyżej
) ma stopień co najwyżej
 więc musi być tożsamościowo równy zeru. Zatem dla każdego
więc musi być tożsamościowo równy zeru. Zatem dla każdego
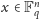 mamy
mamy


Oznaczmy stopień
 przez
przez
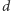 i rozpiszmy
i rozpiszmy
 na części
jednorodne, czyli
na części
jednorodne, czyli

gdzie
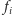 jest wielomianem złożonym z jednomianów stopnia dokładnie
jest wielomianem złożonym z jednomianów stopnia dokładnie
 Nietrudno sprawdzić, że dla dowolnego
Nietrudno sprawdzić, że dla dowolnego
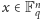 wyraz
wiodący wielomianu
wyraz
wiodący wielomianu
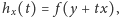 a więc współczynnik
przy
a więc współczynnik
przy
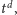 wynosi
wynosi
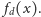 Skoro
Skoro
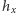 jest równy
tożsamościowo zeru, to ma wszystkie współczynniki równe zeru,
a więc dla każdego
jest równy
tożsamościowo zeru, to ma wszystkie współczynniki równe zeru,
a więc dla każdego
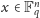 zachodzi
zachodzi
 Jednak
Jednak
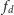 ma stopień
ma stopień
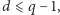 więc gdyby nie był tożsamościowo
równy zeru, to na mocy lematu Schwartza–Zippela mógłby mieć co
najwyżej
więc gdyby nie był tożsamościowo
równy zeru, to na mocy lematu Schwartza–Zippela mógłby mieć co
najwyżej
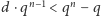 miejsc zerowych. Stąd wniosek, że
miejsc zerowych. Stąd wniosek, że
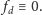 Założyliśmy jednak, że wielomian
Założyliśmy jednak, że wielomian
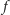 ma stopień
ma stopień
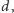 czyli w szczególności
czyli w szczególności
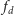 nie jest tożsamościowo równy
zeru – otrzymujemy więc sprzeczność.
nie jest tożsamościowo równy
zeru – otrzymujemy więc sprzeczność.
Wywnioskowaliśmy zatem, że dowolny zbiór Kakeyi
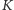 musi mieć
moc
musi mieć
moc
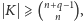 co z dokładnością do wyrazów niższego rzędu
w
co z dokładnością do wyrazów niższego rzędu
w
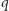 wynosi
wynosi
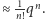 Udowodniliśmy więc hipotezę Kakeyi ze stałą
Udowodniliśmy więc hipotezę Kakeyi ze stałą
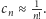
Stosując bardziej wyrafinowany wariant metody wielomianowej – tzw. metodę
krotności – można udowodnić hipotezę Kakeyi z asymptotycznie lepszą stałą
 Z drugiej strony, znane są konstrukcje zbiorów Kakeyi rozmiaru
bliskiego
Z drugiej strony, znane są konstrukcje zbiorów Kakeyi rozmiaru
bliskiego
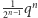 dla dostatecznie dużego
dla dostatecznie dużego

Czytelnikowi zainteresowanemu tym zagadnieniem, a w szczególności innymi zastosowaniami metody wielomianowej, polecamy materiały ze strony http://warsztatywww.wikidot.com/www8:kody-ciala-igly przygotowane przez autorów artykułu.
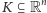
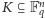

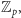 zbiór liczb
od
zbiór liczb
od
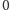 do
do
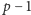 z działaniami dodawania i mnożenia modulo
z działaniami dodawania i mnożenia modulo