Zera funkcji kwadratowych
Niejeden maturzysta marzy zapewne, żeby na egzaminie dojrzałości
rozwiązywać następujące, z pozoru błahe, zadanie: Wyznacz liczbę
miejsc zerowych funkcji
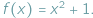 Abiturienta nie zraziłaby
prawdopodobnie nawet drobna przeszkoda, jaką jest wyraźny brak informacji
o dziedzinie funkcji
Abiturienta nie zraziłaby
prawdopodobnie nawet drobna przeszkoda, jaką jest wyraźny brak informacji
o dziedzinie funkcji
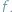 Z uwagi na wszechobecność zbioru
liczb rzeczywistych w obecnym programie nauczania wydaje się, że
o żadnych zerach mowy być nie może. Nawet słynna „delta” nie jest tu
potrzebna.
Z uwagi na wszechobecność zbioru
liczb rzeczywistych w obecnym programie nauczania wydaje się, że
o żadnych zerach mowy być nie może. Nawet słynna „delta” nie jest tu
potrzebna.
Tym, którzy z powodzeniem przejdą przez egzamin maturalny, przyjdzie, być
może, zetknąć się z liczbami zespolonymi. Mają one tę własność, że
wśród nich znajdują się pierwiastki nawet tak opornych funkcji, jak
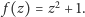 Co więcej, każdy wielomian jednej zmiennej zespolonej
o dowolnych współczynnikach (nie tylko całkowitych) ma pierwiastek
zespolony. Dowód tego ważnego faktu, znanego powszechnie jako Zasadnicze
Twierdzenie Algebry, młodzi adepci matematyki poznają w przynajmniej kilku
odsłonach, nierzadko bardzo nieoczekiwanych.
Co więcej, każdy wielomian jednej zmiennej zespolonej
o dowolnych współczynnikach (nie tylko całkowitych) ma pierwiastek
zespolony. Dowód tego ważnego faktu, znanego powszechnie jako Zasadnicze
Twierdzenie Algebry, młodzi adepci matematyki poznają w przynajmniej kilku
odsłonach, nierzadko bardzo nieoczekiwanych.
Równanie
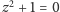 ma dwa pierwiastki zespolone:
ma dwa pierwiastki zespolone:
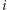 oraz
oraz
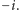 Liczba pierwiastków pokrywa się zatem ze stopniem wielomianu
i nie jest to żaden przypadek. Zamieniając
Liczba pierwiastków pokrywa się zatem ze stopniem wielomianu
i nie jest to żaden przypadek. Zamieniając
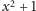 na dowolną inną
funkcję kwadratową, nigdy nie dostaniemy więcej niż dwóch różnych
miejsc zerowych. Co więcej, nie jest to fenomen dotyczący wyłącznie liczb
zespolonych. Okazuje się, że ograniczenie nie powiększy się, o ile założymy
przynajmniej tyle, że zarówno współczynniki, jak i dziedzina funkcji
na dowolną inną
funkcję kwadratową, nigdy nie dostaniemy więcej niż dwóch różnych
miejsc zerowych. Co więcej, nie jest to fenomen dotyczący wyłącznie liczb
zespolonych. Okazuje się, że ograniczenie nie powiększy się, o ile założymy
przynajmniej tyle, że zarówno współczynniki, jak i dziedzina funkcji
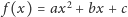 wyposażone są w dowolną strukturę określaną
w algebrze mianem ciała. Jak się jednak okaże „przynajmniej” nie zawsze
znaczy „mało”.
wyposażone są w dowolną strukturę określaną
w algebrze mianem ciała. Jak się jednak okaże „przynajmniej” nie zawsze
znaczy „mało”.
Niepusty zbiór
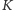 nazwiemy ciałem, jeśli wolno w nim odpowiednio
dodawać i mnożyć pary elementów. Działania te oznaczamy zwykle przez
„
nazwiemy ciałem, jeśli wolno w nim odpowiednio
dodawać i mnożyć pary elementów. Działania te oznaczamy zwykle przez
„
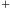 ” oraz „
” oraz „
 ”. Co znaczy „odpowiednio”? Muszą być łączne
i związane znanymi prawami rozdzielności. Każde ciało musi mieć zero,
oznaczane przez „0”, oraz jedynkę, oznaczaną przez „1”. Są one elementami
neutralnymi odpowiednio dodawania i mnożenia, a więc dodawanie zera
i mnożenie przez jedynkę nie zmieniają elementu, który poddajemy tym
operacjom. Każdy element musi mieć element przeciwny, a każdy poza zerem
– element odwrotny. I rzecz dla nas kluczowa: działania „
”. Co znaczy „odpowiednio”? Muszą być łączne
i związane znanymi prawami rozdzielności. Każde ciało musi mieć zero,
oznaczane przez „0”, oraz jedynkę, oznaczaną przez „1”. Są one elementami
neutralnymi odpowiednio dodawania i mnożenia, a więc dodawanie zera
i mnożenie przez jedynkę nie zmieniają elementu, który poddajemy tym
operacjom. Każdy element musi mieć element przeciwny, a każdy poza zerem
– element odwrotny. I rzecz dla nas kluczowa: działania „
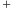 ” i „
” i „
 ”
mają być przemienne.
”
mają być przemienne.
Wspomnieliśmy już o liczbach rzeczywistych i zespolonych. Są to przykłady
ciał nieskończonych. Tymczasem już na zbiorze dwuelementowym można
wprowadzić strukturę ciała. Rozważmy zbiór
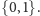 Przyjmijmy, że
działania dodawania i mnożenia określone są zgodnie z następującymi
tabelkami:
Przyjmijmy, że
działania dodawania i mnożenia określone są zgodnie z następującymi
tabelkami:

Nietrudno zidentyfikować powyższe reguły z działaniami na resztach
z dzielenia przez 2. Czytelnik bez trudu sprawdzi, że powyższe warunki zadają
na zbiorze
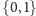 strukturę ciała dwuelementowego, oznaczanego zwykle
przez
strukturę ciała dwuelementowego, oznaczanego zwykle
przez
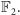 Skoro mamy ciało, możemy rozważać funkcje kwadratowe
i wyznaczać miejsca zerowe. Spójrzmy na funkcję
Skoro mamy ciało, możemy rozważać funkcje kwadratowe
i wyznaczać miejsca zerowe. Spójrzmy na funkcję
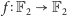 zadaną
wzorem
zadaną
wzorem
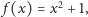 której współczynniki należą przecież do
której współczynniki należą przecież do
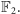 Podstawiając elementy dziedziny, dostajemy:
Podstawiając elementy dziedziny, dostajemy:

Ogólnie, dla każdej liczby pierwszej
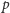 zbiór
zbiór
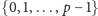 reszt
z dzielenia przez
reszt
z dzielenia przez
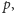 wyposażony w działanie dodawania i mnożenia
reszt, jest ciałem.
wyposażony w działanie dodawania i mnożenia
reszt, jest ciałem.
Analogiczna struktura zadana na zbiorze reszt z dzielenia przez liczbę złożoną ciałem być nie może – zachęcamy Czytelnika do poszukiwania powodu.
Co oznacza bycie pierwiastkiem wielomianu
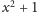 w ciele
w ciele
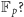 Jest
to, oczywiście, związane z podzielnością przez
Jest
to, oczywiście, związane z podzielnością przez
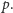 Jeśli rozważymy
zbiór
Jeśli rozważymy
zbiór
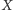 liczb całkowitych, takich, które podniesione do kwadratu
i powiększone o 1 są podzielne przez
liczb całkowitych, takich, które podniesione do kwadratu
i powiększone o 1 są podzielne przez
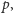 to elementy tego zbioru dają co
najwyżej dwie różne reszty z dzielenia przez
to elementy tego zbioru dają co
najwyżej dwie różne reszty z dzielenia przez
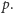 Które dwie? To już
inna historia...
Które dwie? To już
inna historia...
Postawmy jeszcze jedno pytanie. Czy funkcja
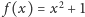 może mieć
nieskończenie wiele miejsc zerowych? Odpowiedź brzmi: tak! Przykład
dziedziny mającej tę własność jest tym bardziej zaskakujący, że znajduje się
bardzo blisko ciał. Mowa tu bowiem o kwaternionach, uogólnieniu liczb
zespolonych, których odkrycie, datowane na rok 1843, przypisuje się
Hamiltonowi. Czym one są?
może mieć
nieskończenie wiele miejsc zerowych? Odpowiedź brzmi: tak! Przykład
dziedziny mającej tę własność jest tym bardziej zaskakujący, że znajduje się
bardzo blisko ciał. Mowa tu bowiem o kwaternionach, uogólnieniu liczb
zespolonych, których odkrycie, datowane na rok 1843, przypisuje się
Hamiltonowi. Czym one są?
Konstruując ciało liczb zespolonych, do zbioru liczb rzeczywistych
dokładaliśmy tajemniczy element
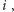 którego kwadrat był równy
którego kwadrat był równy
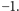 Kwaterniony powstają na podobnej zasadzie, ale zamiast jednego
elementu obcego rozważa się aż trzy. Nazwijmy je
Kwaterniony powstają na podobnej zasadzie, ale zamiast jednego
elementu obcego rozważa się aż trzy. Nazwijmy je
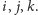 Każdy z nich,
podobnie jak jednostka urojona, ma tę własność, że jego kwadrat to
Każdy z nich,
podobnie jak jednostka urojona, ma tę własność, że jego kwadrat to
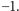 Co więcej, iloczyn dowolnych dwóch równy jest trzeciemu
(z dokładnością do znaku). Dokładniej,
Co więcej, iloczyn dowolnych dwóch równy jest trzeciemu
(z dokładnością do znaku). Dokładniej,

O ile dowolny element w ciele liczb zespolonych wyraża się jako
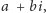 gdzie
gdzie
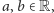 w przypadku kwaternionów dowolny
element przedstawia się jako
w przypadku kwaternionów dowolny
element przedstawia się jako
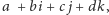 gdzie
gdzie
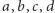 to
dowolne liczby rzeczywiste. Kwaterniony można dodawać i mnożyć
(stosując analogiczną metodę jak dla liczb zespolonych). Działania są łączne,
zachowane są prawa rozdzielności. Znajdą się, rzecz jasna, zero i jedynka.
Niemniej jednak kwaterniony nie są ciałem, a powód podaliśmy już
na starcie. Pogwałcona została przemienność mnożenia. Istotnie,
to
dowolne liczby rzeczywiste. Kwaterniony można dodawać i mnożyć
(stosując analogiczną metodę jak dla liczb zespolonych). Działania są łączne,
zachowane są prawa rozdzielności. Znajdą się, rzecz jasna, zero i jedynka.
Niemniej jednak kwaterniony nie są ciałem, a powód podaliśmy już
na starcie. Pogwałcona została przemienność mnożenia. Istotnie,
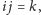 ale
ale
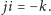 Ta drobna (i jedyna!) różnica – brak
przemienności mnożenia, który wyklucza kwaterniony z klasy ciał – ma
poważne konsekwencje dla zliczania pierwiastków wielomianów.
Ta drobna (i jedyna!) różnica – brak
przemienności mnożenia, który wyklucza kwaterniony z klasy ciał – ma
poważne konsekwencje dla zliczania pierwiastków wielomianów.
Przyjrzyjmy się sprawie dokładniej. Funkcja
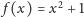 ma na pewno
przynajmniej trzy kwaternionowe zera. Są to elementy
ma na pewno
przynajmniej trzy kwaternionowe zera. Są to elementy
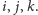 Za dużo jak
na ciało, ale wciąż za mało jak na „nieskończenie wiele”. Podstawiajmy więc
dalej:
Za dużo jak
na ciało, ale wciąż za mało jak na „nieskończenie wiele”. Podstawiajmy więc
dalej:

Nie tylko otrzymaliśmy kolejne miejsce zerowe, lecz także złapaliśmy
nieprzemienność kwaternionów na gorącym uczynku. Otrzymane zero to
skutek reguły mnożenia elementów
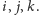 W podobny sposób
możemy otrzymać coraz więcej pierwiastków. Dokładny rachunek pokazuje,
że wśród kwaternionów postaci
W podobny sposób
możemy otrzymać coraz więcej pierwiastków. Dokładny rachunek pokazuje,
że wśród kwaternionów postaci
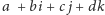 funkcja
funkcja
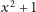 zeruje się dokładnie na tych, w których współczynnik
zeruje się dokładnie na tych, w których współczynnik
 równy jest
równy jest
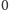 (tzw. kwaterniony czyste), a które leżą na sferze
opisanej równaniem
(tzw. kwaterniony czyste), a które leżą na sferze
opisanej równaniem
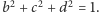
Kwaterniony zaprowadziły nas zatem daleko od początkowych rozważań. Ale
czy aby na pewno? Czy nie ma w tym żadnego podstępu? Pierwiastki przez nas
wskazane, choć jest ich dużo, są bardzo podobne. Wiele z nich różni jedynie
tzw. sprzężenie. Oznacza to, że jeśli utożsamilibyśmy wszystkie pary
pierwiastków
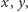 dla których istnieje kwaternion odwracalny
dla których istnieje kwaternion odwracalny
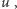 taki, że spełniony jest warunek
taki, że spełniony jest warunek
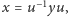 to zostałyby nam
dokładnie... dwa pierwiastki! I nie jest to przypadek, ale całkiem poważne
twierdzenie i właściwość mająca analogię wśród wielomianów wyższych
stopni. Ale o tym to już przy innej okazji...
to zostałyby nam
dokładnie... dwa pierwiastki! I nie jest to przypadek, ale całkiem poważne
twierdzenie i właściwość mająca analogię wśród wielomianów wyższych
stopni. Ale o tym to już przy innej okazji...
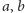 są
elementami ciała, to są nimi także
są
elementami ciała, to są nimi także
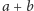 oraz
oraz
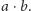
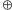 jest przemienne, jeśli dla każdych
jest przemienne, jeśli dla każdych
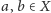 zachodzi równość
zachodzi równość