Konkurs prac uczniowskich
O prawdopodobieństwie, wyznacznikach i pokryciach cyklowych
W tym artykule będziemy się zajmowali obliczaniem wyznaczników macierzy
w dowolnym skończonym ciele
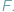 Będziemy także badali, jakie
jest prawdopodobieństwo, że taki wyznacznik dla macierzy z losowo
wpisanymi elementami z ciała
Będziemy także badali, jakie
jest prawdopodobieństwo, że taki wyznacznik dla macierzy z losowo
wpisanymi elementami z ciała
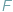 jest różny od
jest różny od
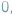 oraz
jakie jest prawdopodobieństwo, że w losowym grafie skierowanym jest
nieparzyście wiele pokryć cyklowych.
oraz
jakie jest prawdopodobieństwo, że w losowym grafie skierowanym jest
nieparzyście wiele pokryć cyklowych.
Jeżeli mamy daną macierz kwadratową z wpisanymi w nią elementami ciała
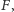 to ciężko na pierwszy rzut oka stwierdzić, czy jej wyznacznik jest
zerowy, czy nie. Sprawa okazuje się dużo prostsza, gdy mamy do czynienia
z macierzą w postaci schodkowej (tzn. z taką, która ma zera poniżej głównej
przekątnej). Wyznacznik takiej macierzy jest zerowy wtedy i tylko wtedy, gdy na
jej głównej przekątnej znajduje się co najmniej jedno
to ciężko na pierwszy rzut oka stwierdzić, czy jej wyznacznik jest
zerowy, czy nie. Sprawa okazuje się dużo prostsza, gdy mamy do czynienia
z macierzą w postaci schodkowej (tzn. z taką, która ma zera poniżej głównej
przekątnej). Wyznacznik takiej macierzy jest zerowy wtedy i tylko wtedy, gdy na
jej głównej przekątnej znajduje się co najmniej jedno
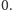 Aby
sprowadzić naszą macierz do postaci schodkowej, użyjemy metody eliminacji
Gaussa. Będziemy wykonywać dwa rodzaje operacji. Pierwszym będzie zamiana
dwóch wierszy miejscami, a drugim będzie dodanie do ustalonego wiersza
innego wiersza pomnożonego przez stałą. Jak wiadomo, operacja drugiego
rodzaju nie zmienia wyznacznika macierzy, operacja pierwszego rodzaju
natomiast zmienia jego znak, a więc nie zmienia tego, czy wyznacznik jest
zerowy, czy nie.
Aby
sprowadzić naszą macierz do postaci schodkowej, użyjemy metody eliminacji
Gaussa. Będziemy wykonywać dwa rodzaje operacji. Pierwszym będzie zamiana
dwóch wierszy miejscami, a drugim będzie dodanie do ustalonego wiersza
innego wiersza pomnożonego przez stałą. Jak wiadomo, operacja drugiego
rodzaju nie zmienia wyznacznika macierzy, operacja pierwszego rodzaju
natomiast zmienia jego znak, a więc nie zmienia tego, czy wyznacznik jest
zerowy, czy nie.
Sprowadzając macierz do postaci schodkowej, najpierw musimy zadbać o to,
aby w górnym lewym rogu naszej macierzy znalazł się jakiś niezerowy
element. Jeżeli w pierwszej kolumnie są same zera, to przerywamy nasz
algorytm, gdyż wyznacznik naszej macierzy na pewno jest równy
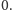 W przeciwnym przypadku, jeżeli w górnym lewym rogu jest już
niezerowy element, to nic nie robimy, a jeśli nie, to zamieniamy pierwszy
wiersz z którymś, w którym w pierwszej kolumnie znajduje się niezerowy
element. Następnie musimy zadbać o to, aby w tej kolumnie nie było
więcej niezerowych elementów, zatem jeżeli w górnym lewym rogu
znajduje się element
W przeciwnym przypadku, jeżeli w górnym lewym rogu jest już
niezerowy element, to nic nie robimy, a jeśli nie, to zamieniamy pierwszy
wiersz z którymś, w którym w pierwszej kolumnie znajduje się niezerowy
element. Następnie musimy zadbać o to, aby w tej kolumnie nie było
więcej niezerowych elementów, zatem jeżeli w górnym lewym rogu
znajduje się element
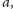 a w innym wierszu w pierwszej kolumnie
znajduje się element
a w innym wierszu w pierwszej kolumnie
znajduje się element
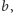 to musimy do tego wiersza dodać pierwszy
wiersz pomnożony przez
to musimy do tego wiersza dodać pierwszy
wiersz pomnożony przez
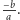 Zatem zrobiliśmy już wszystko, co
mieliśmy zrobić z pierwszym wierszem i pierwszą kolumną, i dalej
ograniczamy się do reszty naszej macierzy, dla której powtarzamy to
postępowanie. Kończymy je w momencie, gdy w macierzy, która nam
pozostała, w pierwszej kolumnie są same zera (wtedy wyznacznik równa się
Zatem zrobiliśmy już wszystko, co
mieliśmy zrobić z pierwszym wierszem i pierwszą kolumną, i dalej
ograniczamy się do reszty naszej macierzy, dla której powtarzamy to
postępowanie. Kończymy je w momencie, gdy w macierzy, która nam
pozostała, w pierwszej kolumnie są same zera (wtedy wyznacznik równa się
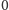 ) lub gdy szczęśliwie dojdziemy do końca (wtedy wyznacznik jest
niezerowy).
) lub gdy szczęśliwie dojdziemy do końca (wtedy wyznacznik jest
niezerowy).
Jak ta metoda może nam pomóc w obliczeniu prawdopodobieństwa, że
dla kwadratowej macierzy
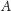 rozmiaru
rozmiaru
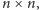 w której
każde pole jest wpisany z równym prawdopodobieństwem jakiś
element ciała
w której
każde pole jest wpisany z równym prawdopodobieństwem jakiś
element ciała
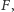 jej wyznacznik jest niezerowy? Oznaczmy liczbę
elementów ciała
jej wyznacznik jest niezerowy? Oznaczmy liczbę
elementów ciała
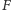 przez
przez
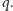 Zastanówmy się najpierw, jakie jest
prawdopodobieństwo tego, że będziemy mogli wykonać pierwszą fazę
algorytmu, czyli że w pierwszej kolumnie znajdzie się jakiś niezerowy
element. Abyśmy nie mogli jej wykonać, w każdym z
Zastanówmy się najpierw, jakie jest
prawdopodobieństwo tego, że będziemy mogli wykonać pierwszą fazę
algorytmu, czyli że w pierwszej kolumnie znajdzie się jakiś niezerowy
element. Abyśmy nie mogli jej wykonać, w każdym z
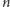 pól
pierwszej kolumny musi znaleźć się
pól
pierwszej kolumny musi znaleźć się
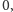 a znajduje się ono w każdym
polu z prawdopodobieństwem
a znajduje się ono w każdym
polu z prawdopodobieństwem
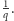 Zatem prawdopodobieństwo
tego, że będziemy mogli wykonać pierwszą fazę algorytmu, wynosi
Zatem prawdopodobieństwo
tego, że będziemy mogli wykonać pierwszą fazę algorytmu, wynosi
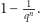 Nietrudno przekonać się o tym, że nie tylko w pierwszej, ale
w dowolnej,
Nietrudno przekonać się o tym, że nie tylko w pierwszej, ale
w dowolnej,
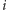 -tej fazie algorytmu, rozkład prawdopodobieństwa
wartości znajdujących się w polach
-tej fazie algorytmu, rozkład prawdopodobieństwa
wartości znajdujących się w polach
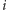 -tej kolumny, jest jednostajny.
Stosując analogiczną argumentację wnioskujemy, iż prawdopodobieństwo tego,
że będziemy mogli wykonać
-tej kolumny, jest jednostajny.
Stosując analogiczną argumentację wnioskujemy, iż prawdopodobieństwo tego,
że będziemy mogli wykonać
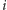 -tą fazę, o ile będziemy mogli wykonać
pierwsze
-tą fazę, o ile będziemy mogli wykonać
pierwsze
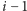 faz, jest równe
faz, jest równe

Stąd otrzymujemy końcowy wynik, że prawdopodobieństwo wykonania
całego algorytmu, czyli prawdopodobieństwo tego, że wyznacznik macierzy
będzie różny od
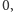 jest równe
jest równe

Zajmijmy się teraz następującym problemem. Rozważmy graf skierowany o
 wierzchołkach, w którym dla każdej uporządkowanej pary liczb
wierzchołkach, w którym dla każdej uporządkowanej pary liczb
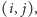 takiej że
takiej że
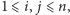 krawędź skierowana od wierzchołka
krawędź skierowana od wierzchołka
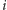 do wierzchołka
do wierzchołka
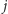 występuje z prawdopodobieństwem
występuje z prawdopodobieństwem
 (w szczególności, w tym grafie mogą występować pętle). Jakie
jest prawdopodobieństwo tego, że w tym grafie jest nieparzysta liczba
pokryć cyklowych?
(w szczególności, w tym grafie mogą występować pętle). Jakie
jest prawdopodobieństwo tego, że w tym grafie jest nieparzysta liczba
pokryć cyklowych?
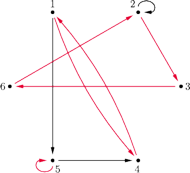
A czym właściwie są pokrycia cyklowe? Otóż pokrycie cyklowe to taki zbiór
 krawędzi grafu, że z każdego wierzchołka wychodzi dokładnie jedna
krawędź i do każdego wierzchołka wchodzi dokładnie jedna krawędź
z tego zbioru. Przedstawia się ono jako zbiór rozłącznych cykli o łącznej
długości
krawędzi grafu, że z każdego wierzchołka wychodzi dokładnie jedna
krawędź i do każdego wierzchołka wchodzi dokładnie jedna krawędź
z tego zbioru. Przedstawia się ono jako zbiór rozłącznych cykli o łącznej
długości
 Każde pokrycie cyklowe możemy utożsamiać z
Każde pokrycie cyklowe możemy utożsamiać z
 -elementową permutacją
-elementową permutacją
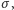 w której
w której
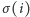 jest numerem
wierzchołka, do którego wchodzi krawędź wychodząca z wierzchołka
o numerze
jest numerem
wierzchołka, do którego wchodzi krawędź wychodząca z wierzchołka
o numerze
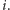 Permutacja
Permutacja
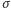 reprezentuje pokrycie cyklowe, jeżeli
dla każdego
reprezentuje pokrycie cyklowe, jeżeli
dla każdego
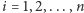 istnieje krawędź z wierzchołka
istnieje krawędź z wierzchołka
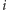 do
wierzchołka
do
wierzchołka
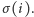
Zapiszmy nasz graf w postaci macierzy sąsiedztwa
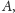 czyli macierzy
kwadratowej o wymiarach
czyli macierzy
kwadratowej o wymiarach
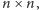 w której w polu
w której w polu
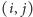 jest
jest
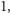 jeżeli istnieje krawędź od wierzchołka
jeżeli istnieje krawędź od wierzchołka
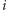 do wierzchołka
do wierzchołka
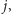 a w przeciwnym przypadku jest tam
a w przeciwnym przypadku jest tam
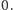 A jak na tę
macierz przenoszą się pokrycia cyklowe? Rozpatrzmy pewne pokrycie
cyklowe i zaznaczmy w naszej macierzy pola odpowiadające krawędziom
należącym do pokrycia. Będzie to
A jak na tę
macierz przenoszą się pokrycia cyklowe? Rozpatrzmy pewne pokrycie
cyklowe i zaznaczmy w naszej macierzy pola odpowiadające krawędziom
należącym do pokrycia. Będzie to
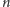 takich pól, że żadne dwa pola
nie znajdują się w tym samym wierszu ani w tej samej kolumnie i, w dodatku,
wszystkie te pola mają wartość
takich pól, że żadne dwa pola
nie znajdują się w tym samym wierszu ani w tej samej kolumnie i, w dodatku,
wszystkie te pola mają wartość
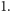 Zatem iloczyn liczb w tych
polach będzie równy
Zatem iloczyn liczb w tych
polach będzie równy
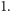 A co dzieje się z permutacjami, którym
nie odpowiadają pokrycia cyklowe? Jeżeli zaznaczymy w analogiczny
sposób w naszej macierzy pola odpowiadające potencjalnym krawędziom
z tej permutacji, to skoro nie reprezentowała ona pokrycia cyklowego,
to w co najmniej jednym zaznaczonym polu znajdzie się
A co dzieje się z permutacjami, którym
nie odpowiadają pokrycia cyklowe? Jeżeli zaznaczymy w analogiczny
sposób w naszej macierzy pola odpowiadające potencjalnym krawędziom
z tej permutacji, to skoro nie reprezentowała ona pokrycia cyklowego,
to w co najmniej jednym zaznaczonym polu znajdzie się
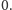 W takim
razie iloczyn liczb w tych polach będzie równy
W takim
razie iloczyn liczb w tych polach będzie równy
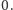 Możemy
zatem wysunąć wniosek, że liczba pokryć cyklowych w tym grafie jest
równa
Możemy
zatem wysunąć wniosek, że liczba pokryć cyklowych w tym grafie jest
równa

gdzie
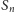 to zbiór wszystkich
to zbiór wszystkich
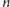 -elementowych permutacji, a
-elementowych permutacji, a
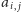 to wartość pola
to wartość pola
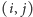 w macierzy sąsiedztwa. Powyższą
liczbę nazywa się też permanentem macierzy
w macierzy sąsiedztwa. Powyższą
liczbę nazywa się też permanentem macierzy
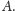 Przypatrzmy się teraz
wzorowi permutacyjnemu na wyznacznik macierzy:
Przypatrzmy się teraz
wzorowi permutacyjnemu na wyznacznik macierzy:

gdzie
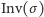 jest liczbą inwersji w permutacji
jest liczbą inwersji w permutacji
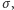 ale dla nas
istotne będzie to, że
ale dla nas
istotne będzie to, że
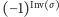 może przyjmować tylko wartości
może przyjmować tylko wartości
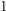 i
i
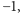 a skoro te dwie liczby są tej samej parzystości, zatem
permanent i wyznacznik macierzy całkowitoliczbowej są tej samej parzystości.
Zauważmy jeszcze, że to, czy wyznacznik takiej macierzy sąsiedztwa jest
parzysty, to po prostu pytanie, czy wyznacznik tej macierzy jest zerowy, jeżeli
potraktujemy macierz sąsiedztwa jako macierz nad ciałem
a skoro te dwie liczby są tej samej parzystości, zatem
permanent i wyznacznik macierzy całkowitoliczbowej są tej samej parzystości.
Zauważmy jeszcze, że to, czy wyznacznik takiej macierzy sąsiedztwa jest
parzysty, to po prostu pytanie, czy wyznacznik tej macierzy jest zerowy, jeżeli
potraktujemy macierz sąsiedztwa jako macierz nad ciałem
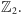 W dodatku,
sposób, w jaki losowaliśmy krawędzie grafu, odpowiada sposobowi, w jaki
losowaliśmy elementy macierzy we wcześniejszej części artykułu.
Z połączenia tych faktów otrzymujemy wniosek, że prawdopodobieństwo
tego, że liczba pokryć cyklowych naszego grafu jest nieparzysta, jest
równe
W dodatku,
sposób, w jaki losowaliśmy krawędzie grafu, odpowiada sposobowi, w jaki
losowaliśmy elementy macierzy we wcześniejszej części artykułu.
Z połączenia tych faktów otrzymujemy wniosek, że prawdopodobieństwo
tego, że liczba pokryć cyklowych naszego grafu jest nieparzysta, jest
równe
