Powiedzmy, że nasz układ wygląda tak:

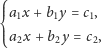
przy czym współczynnik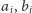i i 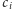  są całkowite. Korzystając ze wspomnianej metody, należy obliczyć trzy wyznaczniki, które zwyczajowo oznacza się jako 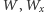 i :

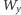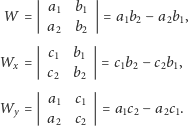
Zauważmy, że jeśli wszystkie współczynniki były całkowite, to obliczone wyznaczniki także są całkowite. Obliczywszy te trzy wartości, mamy już właściwie gotowe rozwiązanie. Przypomnijmy: jeśli 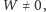 to układ ma jedno rozwiązanie:

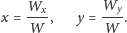
Jeśl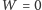i  i 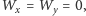  to układ ma nieskończenie wiele rozwiązań, a w przeciwnym przypadku ( 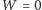 i któryś z wyznaczników 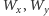 jest niezerowy) układ jest sprzeczny, czyli nie ma rozwiązań.

Przykładowo, zobaczmy, jak działa podana metoda dla poniższego, trochę nietypowego układu równań:

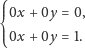
Łatwo sprawdzamy, że wówczas 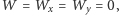 czyli układ ma nieskończenie wiele rozwiązań. Problem polega na tym, że trudno jest właściwie wskazać jakiekolwiek z tych nieskończenie wielu rozwiązań. Coś tu nie gra!

Najwyraźniej zapomnieliśmy o jakichś dodatkowych uwarunkowaniach wykorzystywanej metody. Jak w takiej sytuacji poradzi sobie informatyk? To proste: wpisze w ulubioną wyszukiwarkę internetową hasło „metoda wyznaczników” i przejrzy pierwszych kilka wyników wyszukiwania. Niestety, lektura tak znalezionych stron internetowych nie rozwiązuje naszej zagadki – najwyraźniej zastosowaliśmy metodę wyznaczników zupełnie poprawnie. A więc co jest nie tak?