Na sprawę można spojrzeć inaczej: na ile sposobów można zmienić położenie takiego banknotu? Odpowiedź, wbrew pozorom, też będzie: cztery. Trzy znajdujemy łatwo: symetria względem pionowej osi 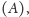symetria względem poziomej osi 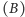i obrót o 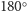względem środka, czyli symetria środkowa A czwarty sposób? No właśnie: …nie ruszać go wcale 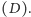Taki układ ruchów, który prowadzi do każdego możliwego położenia banknotu to jego izometrie własne lub jego ruchy.

Mają one ciekawą własność: jeśli wykonamy po kolei kilka z nich, to zawsze okaże się, że końcowy wynik można było uzyskać za pomocą tylko jednego. Proszę sprawdzić, że ta tabelka, mówiąca, co wyjdzie z wykonania kolejno dwóch takich ruchów, nie kłamie.

Za jej pomocą możemy obliczyć, jak będzie leżał banknot po kilku ruchach, bez posługiwania się banknotem. Na przykład

czyli zamiast wykonywać skomplikowane operacje opisane na początku wystarczyło tylko raz obrócić banknot. Jak to zostało obliczone? Otóż przy takich obliczeniach można dowolnie wstawiać nawiasy, więc liczyliśmy tak

Jak widać, te cztery ruchy, oznaczone przez nas tworzą układ zamknięty. W takiej sytuacji mówimy, że tworzą one grupę. Jest to grupa o czterech elementach.

Można by się zastanowić, czy jest to jedyna grupa czteroelementowa, to znaczy, czy każde inne zamknięte cztery ruchy różnić się będą od ruchów banknotu tylko obrazkiem czy nazwami.

Spróbujmy wykonać eksperyment.

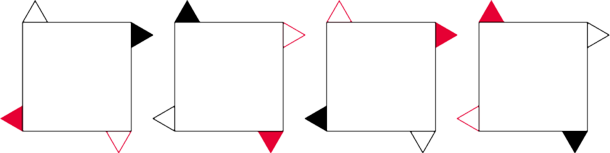
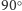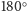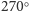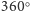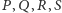Tym razem zastanowimy się, jak można przekładać kwadrat, co ma cztery rogi. Bez trudu stwierdzimy, że tym razem odwrócić go na drugą stronę się nie da – rogi nie pozwalają. Ale można go obrócić o  , , i  (lub w ogóle go nie ruszać, co na jedno wychodzi). Niech będą to ruchy . Ułóżmy dla nich tabelkę.

---

Tabelka wygląda trochę inaczej, ale może można tak poprzestawiać wiersze lub kolumny tej tabelki, by stała się taka sama jak ta poprzednia?

Baczniejsze przyjrzenie się obu tabelkom (to nawet lepiej, że oglądać je będziemy z osobna) pokazuje, że jest to jednak inna tabelka. Tam, na poprzedniej stronie, wszystkie ruchy miały tę własność, że jak się je wykonało dwa razy, to wychodziło to samo:

a tutaj tak nie jest. Oznacza to, że grupa rogatego kwadratu jest inna od grupy banknotu, bo ma inne własności. Mamy więc już dwie różne grupy o czterech elementach. A czy jest ich więcej?

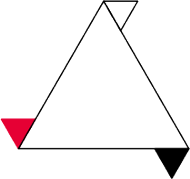
A czy grupa może mieć mniej niż cztery elementy? Oczywiście. Na przykład grupa rogatego trójkąta równobocznego. Proszę sprawdzić, że to jest jej tabelka.

Jest ona podobna do tabelki rogatego kwadratu – tak samo linie z lewego dołu do prawej góry składają się z jednakowych liter. A jakie właściwie ruchy oznaczają litery ?

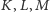A czy jest więcej grup trójelementowych niż ta jedna?

Każdy zgadnie z łatwością, jak napisać tabelkę rogatego pięciokąta foremnego. A czy grup pięcioelementowych jest więcej?

Zostawię to – jako bardzo trudne pytanie – Czytelnikom.

Jako ćwiczenie proponuję natomiast ustalenie liczby ruchów i napisanie tabelki dla ruchów nierogatego trójkąta równobocznego. Każdy dostrzega, że może to być coś trochę podobnego do banknotu, bo trójkąt będzie się mógł obracać „na lewą stronę”. Ale i do rogatego trójkąta też.

Po wykonaniu tego ćwiczenia będzie można z łatwością stwierdzić, że grup sześcioelementowych jest co najmniej dwie.