Możemy wziąć także bardzo wyjątkowy ciąg o długości zero, nazywany słowem pustym. Niektórzy zajmują się też nieskończonymi słowami, ale to inna historia. Dla nas każde słowo ma długość będącą liczbą całkowitą nieujemną.

A właściwie jakie litery dopuszczamy? Czy pozwalamy tylko na alfabet angielski, czy akceptujemy wszelkie ogonki, kropki, kreślenia i akcenty? Otóż możemy ustalić, co nam się podoba, ale trzeba to zrobić na początku zabawy. Czyli zaczynamy od wybrania alfabetu – zestawu znaków, z których będziemy składać słowa. Może to być alfabet angielski, może być polski, może być zbiór egipskich hieroglifów albo nawet zestaw 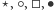. Na przykład komputery, wczytując program, pracują zwykle na słowach nad alfabetem złożonym z małych i dużych liter, cyfr i kilku znaków specjalnych (np. kropka, podkreślenie). A zapisując dane, używają dwuliterowego alfabetu: 0 i 1. Wszystkie znaki w alfabecie, jakkolwiek by one nie wyglądały, będziemy nazywać literami.

Jeśli mamy wybrany alfabet, to umiemy budować słowa, więc możemy też tworzyć języki. Językiem będzie dla nas po prostu zbiór słów zbudowanych z liter wybranego alfabetu. Może być skończony, tak jak zbiór wszystkich słów języka polskiego albo język nad alfabetem 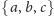złożony z czterech słów 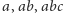i 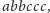albo też język złożony tylko ze słowa pustego. Ale może być nieskończony. Dla dowolnego alfabetu możemy mianowicie wziąć zbiór wszystkich słów, które da się poskładać z jego liter. Poza jednym wyjątkiem – kiedy alfabet ma zero liter i jedyne słowo nad nim to słowo puste – tak utworzony język jest nieskończony.

Przyjrzyjmy się najprostszemu przypadkowi, który ma szanse być ciekawy: alfabetowi złożonemu z jednej litery 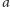 . Możemy napisać słowo jednoliterowe 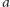 , dwuliterowe 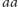 , trzyliterowe 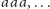Wszystkie słowa, czyli pełny język nad tym alfabetem, to ciągi powtórzeń litery 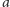 . Słowo puste, oznaczane tradycyjnie  , możemy rozumieć jako ,,zero powtórzeń litery 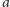 ”. Ale są też inne języki nieskończone nad tym alfabetem, mniejsze od pełnego, czyli będące jego podzbiorami. 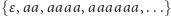Na przykład język słów o parzystej długości , język słów o nieparzystej długości 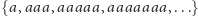, język słów o długościach będących liczbami pierwszymi, język słów o długościach podzielnych przez 157, język słów o długościach będących sześcianami liczb nieparzystych 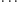Mamy mnóstwo możliwości. 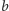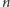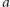A jeśli weźmiemy większy alfabet, chociażby dwuliterowy  i  , to pojawią się takie przykłady, jak język słów mających na początku  liter  , a dalej tyle samo liter  :

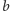język słów zawierających dokładnie jedną literę  :

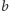czy język słów zawierających przynajmniej dwa razy więcej liter 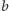 niż  :

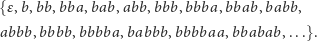Podaliśmy tylko po kilka krótkich słów, ale na pewno, Czytelniku, umiesz te listy przedłużyć, a pewnie też znaleźć algorytm wypisywania słów z każdego z podanych języków, tak żeby żadnego nie pominąć.

Trudno się spodziewać, aby wszystkie języki były tak samo interesujące. Pewnie, na przykład, częściej umiemy wykazać jakieś ciekawe własności języka określonego, jak wyżej, jakąś regułą niż losowego zbioru słów. Dobrym sposobem opisywania porządnych języków są wzory składające się z liter wybranego alfabetu, trzech symbol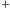i ,   i  , o których za chwilę opowiemy, i, jak zwykle, nawiasów dla zaznaczenia kolejności działań. Takie wzory na konstrukcję języka nazywają się wyrażeniami regularnymi, a języki, które za ich pomocą można opisać, to języki regularne. Są to najporządniejsze z interesujących języków – zwykle, żeby język wyrażał coś ciekawego, musi mieć bardziej skomplikowaną strukturę. Nie zawsze: budowa lekserów (części kompilatorów) jest oparta na językach regularnych, ale już parsery, wykonujące kolejny po analizie leksykalnej krok kompilacji, używają języków opisanych bardziej złożonymi ,,równaniami” niż wyrażenia regularne.

Zajmijmy się naszymi regułami. Można się domyślić, że 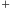 oznacza sumowanie dwóch języków, czyli wrzucenie do jednego języka wszystkich słów z obu danych zbiorów. Dalej,  to też operacja na dwóch językach – nowy język to sklejenia wszystkich słów z pierwszego języka ze wszystkimi z drugiego. Kropkę w zapisie najczęściej się pomija, tak jak znak mnożenia w arytmetyce. Na przykład,

Natomiast to operacja na jednym języku. Nowy język składa się ze wszystkich sklejeń dowolnej długości słów z podanego języka. Czyli, na przykład, zbiór wszystkich słów złożonych z litery 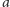 zapisuje się jako 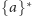 , a zbiór wszystkich słów z liter 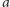,  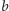 i  to  .

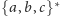Teraz jeszcze trzeba się przyzwyczaić do tego, że symbol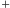i ,   i  będziemy używać nie tylko do języków, ale też do wyrażeń opisujących języki. Czyli przez 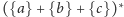rozumiemy zastosowanie operacji  do języka 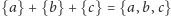. 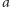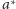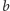Nawiasy klamrowe wokół pojedynczych słów będziemy dla wygody opuszczać, więc ostatecznie wyrażenie opisujące pełny język nad alfabetem  to po prostu  , a wyrażenie dla pełnego języka nad alfabetem ,  ,  to  .

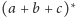A wyrażenia dla innych języków? Zacznijmy od alfabetu jednoliterowego i słów o parzystej długości. Każde takie słowo można podzielić na pary 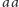 , czyli jest ono sklejeniem pewnej liczby słów 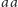 . Wobec tego odpowiednim wyrażeniem regularnym jest 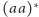 . Ponieważ obejmuje też możliwość sklejenia zera słów z danego języka, to nie musimy się osobno martwić o słowo puste.

Teraz słowa o długości nieparzystej. Jeśli obetniemy pierwszą literę 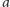 z takiego słowa, to zostanie słowo o parzystej długości, czyli ten język powstaje przez sklejanie litery 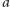 ze słowami z języka z poprzedniego przykładu. Wystarczy więc dokleić literę 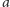 do opisanego wyżej wyrażenia: 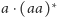. A gdybyśmy napisali 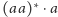? Jak widać, jeden język może być opisywany przez wiele wyrażeń regularnych.

Z pewnością już wiesz, Czytelniku, że język słów o długości podzielnej przez 157 jest opisywany przez wyrażenie 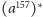 , gdzie 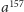zastępuje, oczywiście, odpowiednio długi ciąg, i potrafisz podać wyrażenie dla języka słów o długościach dających resztę 19 z dzielenia przez 91. Co z wyrażeniem dla słów o długościach będących liczbami pierwszymi? Lepiej będzie poszukać dowodu, że takie wyrażenie nie istnieje

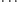
Język nad alfabetem ,  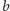złożony ze słów z dokładnie jedną literą 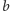 konstruujemy tak:
najpierw piszemy pewną liczbę liter 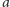 (może zero), później wstawiamy 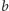 i kończymy ciągiem 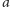 (znów może pustym). Czyli początek i koniec zapisujemy jako 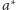 , a całe wyrażenie to 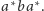Możemy też opisać zbiór słów (nad dwuliterowym alfabetem), w których żadna litera nie występuje trzy razy pod rząd. Ten warunek oznacza, że litery 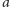 i 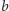 występują blokami co najwyżej dwuelementowymi. Weźmy słowo zaczynające się i kończące literą 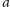 . Wtedy początek to 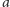lub 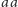 . Jeśli słowo się na tym nie kończy, to dalej mamy 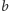lub 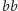 , potem znów 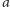lub 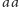 i ta sytuacja może się powtarzać. Wobec tego słowa z naszego języka zaczynające się i kończące 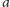 są opisywane wyrażeniem 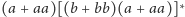. Pozostałe trzy przypadki: słowa zaczynające się 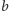 i kończące 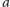 , zaczynające i kończące 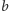 oraz zaczynające 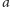 i kończące 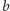 możemy opisać podobnie i dodać wyrażenia definiujące cztery części języka:

Jak opisać język zawierający trzy kolejne wystąpienia pewnej litery? A język słów o nieparzystej długości? Albo język słów, w których liter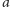a  pojawia się nieparzystą liczbę razy? Można rozważać alfabet dwuliterowy, a można większy. Podpowiemy jeszcze, że wyrażeń dla pozostałych przykładów z poprzedniej strony nie ma sensu szukać nawet w długie zimowe wieczory. Ale warto pomyśleć nad dowodem, że ich nie ma.