Drobiazgi
Reguła czy przypadek?
Gdy do wielomianu 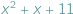 podstawiać będziemy kolejno liczby
podstawiać będziemy kolejno liczby 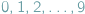 , otrzymamy
, otrzymamy 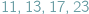 ,
, 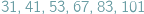 - same liczby pierwsze. Reguła czy przypadek?
- same liczby pierwsze. Reguła czy przypadek?
Nie, to nie jest reguła. Dla 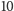 już tak nie będzie: wartość wielomianu dla
już tak nie będzie: wartość wielomianu dla 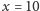 dzieli się przez
dzieli się przez 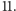
To akurat dziwić nie powinno - każdy wielomian 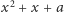 dla
dla 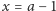 dzieli się przez
dzieli się przez 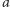 , ponieważ
, ponieważ 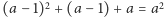 .
.
Ale Czytelnik Dociekliwy zauważy, że różnice kolejnych wartości to kolejne liczby parzyste: 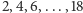 . Czy to też reguła? I to okazuje się także prawidłowością, bowiem
. Czy to też reguła? I to okazuje się także prawidłowością, bowiem 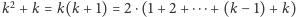 , a więc wartości każdego wielomianu
, a więc wartości każdego wielomianu 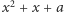 przy podstawieniu kolejnych liczb naturalnych
przy podstawieniu kolejnych liczb naturalnych 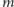 i
i 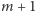 różnić się będą o
różnić się będą o 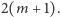
No to może wreszcie i fakt, że podstawiając kolejne liczby naturalne 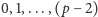 do wielomianu
do wielomianu 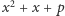 , gdzie
, gdzie 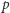 jest - jak
jest - jak 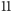 - liczbą pierwszą, otrzymujemy same liczby pierwsze, też jest prawidłowością? Np. dla
- liczbą pierwszą, otrzymujemy same liczby pierwsze, też jest prawidłowością? Np. dla 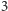 czy
czy 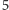 się zgadza!
się zgadza!
Okazuje się, że nie: poza wymienionymi trzema liczbami pierwszymi jest tak jeszcze tylko dla 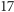 i
i 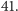 Tyle że nie jest to, oczywiście, przypadek. Ale dowód tego faktu nie jest prosty, choć - zapewne - może sprawić Czytelnikowi Studiującemu wiele satysfakcji.
Tyle że nie jest to, oczywiście, przypadek. Ale dowód tego faktu nie jest prosty, choć - zapewne - może sprawić Czytelnikowi Studiującemu wiele satysfakcji.