Zadanie ZM-1436
o zadaniu...
- Publikacja w Delcie: październik 2014
- Publikacja elektroniczna: 31-10-2014
Niech liczby 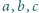 z przedziału
z przedziału 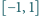 spełniają
spełniają
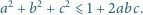
Pokazać, że dla każdej liczby całkowitej 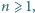
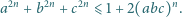
Niech liczby 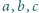 z przedziału
z przedziału 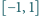 spełniają
spełniają
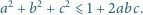
Pokazać, że dla każdej liczby całkowitej 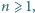
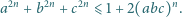
Ile jest takich macierzy 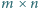 o wyrazach
o wyrazach 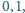 że w każdym wierszu i w każdej kolumnie jest parzysta liczba jedynek?
że w każdym wierszu i w każdej kolumnie jest parzysta liczba jedynek?
Niech 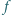 będzie wielomianem stopnia
będzie wielomianem stopnia 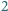 o całkowitych współczynnikach. Wiadomo, że
o całkowitych współczynnikach. Wiadomo, że 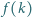 jest podzielne przez
jest podzielne przez 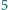 dla każdej liczby całkowitej
dla każdej liczby całkowitej 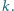 Udowodnić, że wówczas każdy współczynnik
Udowodnić, że wówczas każdy współczynnik 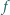 jest podzielny przez
jest podzielny przez 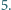
Wyznacz najmniejszą wartość funkcji kwadratowej 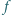 danej wzorem
danej wzorem 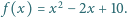
Rozwiąż równanie 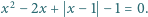
Dane są takie liczby rzeczywiste 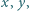 że
że 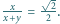 Oblicz
Oblicz 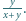
Niech 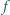 będzie wielomianem o współczynnikach całkowitych o stopniu co najmniej 1. Wykaż, że jeśli
będzie wielomianem o współczynnikach całkowitych o stopniu co najmniej 1. Wykaż, że jeśli  i
i 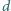 są różnymi liczbami całkowitymi, to
są różnymi liczbami całkowitymi, to  dzieli
dzieli 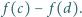
Zbadaj, czy istnieje taki wielomian 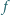 stopnia 3 o współczynnikach całkowitych, że
stopnia 3 o współczynnikach całkowitych, że 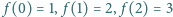 oraz
oraz 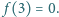
Niech 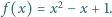 Znajdź wszystkie wartości
Znajdź wszystkie wartości 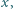 dla których
dla których 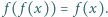
Zadanie 684 zaproponował pan Tomasz Ordowski.
Wykazać, że dla żadnej pary różnych liczb pierwszych 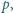
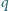 układ równań
układ równań
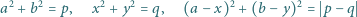
nie ma rozwiązań w liczbach całkowitych 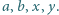
Rozstrzygnąć, czy dla każdych trzech wektorów jednostkowych
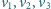 w przestrzeni da się dobrać zestaw trzech znaków
w przestrzeni da się dobrać zestaw trzech znaków
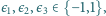 tak aby długość wektora
tak aby długość wektora
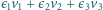 wynosiła
co najmniej
wynosiła
co najmniej
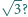
Zadanie 668 zaproponował pan Michał Kremzer.
Czy istnieje podzbiór właściwy zbioru liczb wymiernych dodatnich, w którym wykonalne są działania mnożenia i dzielenia, nie zawierający się w żadnym innym podzbiorze właściwym zbioru liczb wymiernych dodatnich, w którym wykonalne są powyższe działania?
Zadanie 666 zaproponował pan Witold Bednarek z Łodzi.
Niech
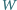 będzie wielomianem stopnia
będzie wielomianem stopnia
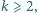 o współczynnikach
całkowitych nieujemnych. Zakładamy, że dla każdej liczby naturalnej
o współczynnikach
całkowitych nieujemnych. Zakładamy, że dla każdej liczby naturalnej
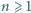 wartość
wartość
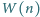 jest
jest
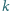 -tą potęgą liczby całkowitej
nieujemnej. Udowodnić, że
-tą potęgą liczby całkowitej
nieujemnej. Udowodnić, że
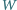 ma postać
ma postać
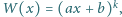 gdzie
gdzie
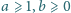 są liczbami całkowitymi.
są liczbami całkowitymi.
Znaleźć wszystkie funkcje
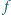 postaci
postaci
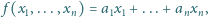
dla pewnych
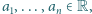 które na zbiorze
które na zbiorze
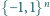 przyjmują
tylko dwie wartości:
przyjmują
tylko dwie wartości:
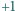 lub
lub
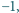 tzn. takie, że jeśli
tzn. takie, że jeśli
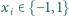 dla
dla
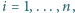 to
to
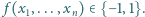
Niech wielomian
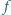 postaci
postaci
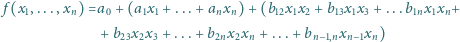
przyjmuje na zbiorze
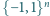 tylko dwie wartości
tylko dwie wartości
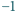 lub
lub
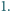 Udowodnić, że suma kwadratów jego współczynników wynosi
Udowodnić, że suma kwadratów jego współczynników wynosi
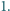
Czy istnieje wielomian
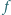 zadany wzorem
zadany wzorem
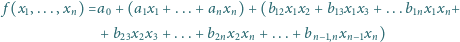
taki że dokładnie trzy spośród jego współczynników
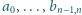 są
niezerowe, i o tej własności, że na zbiorze
są
niezerowe, i o tej własności, że na zbiorze
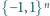 przyjmuje on tylko
wartości
przyjmuje on tylko
wartości
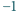 i
i
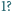 A jeśli założymy, że dokładnie cztery
współczynniki mają być niezerowe?
A jeśli założymy, że dokładnie cztery
współczynniki mają być niezerowe?
Wielomian
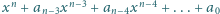 ma współczynniki
rzeczywiste
ma współczynniki
rzeczywiste
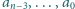 nie wszystkie równe
nie wszystkie równe
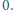 Udowodnić, że
ma on mniej niż
Udowodnić, że
ma on mniej niż
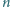 pierwiastków rzeczywistych.
pierwiastków rzeczywistych.
Liczby rzeczywiste
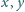 spełniają równość
spełniają równość
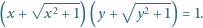
Udowodnić, że
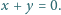
Ile wynosi suma współczynników wielomianu

Zadanie 638 zaproponował pan Paweł Kubit z Krakowa.
Liczby dodatnie
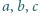 spełniają warunek
spełniają warunek
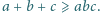 Udowodnić,
że co najwyżej jedna z liczb
Udowodnić,
że co najwyżej jedna z liczb
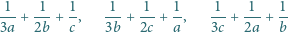
jest mniejsza od 1.
Mówimy, że funkcja
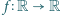 ma cykl długości
ma cykl długości
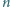 o początku
o początku
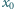 , gdy istnieje takie
, gdy istnieje takie
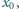 że liczby
że liczby
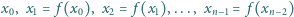 są parami różne, zaś
są parami różne, zaś
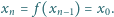
Udowodnić, że jeśli wielomian o współczynnikach całkowitych ma
cykl o początku będącym liczbą całkowitą, to jest on długości
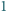 lub
lub
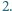
Dane są liczby rzeczywiste
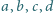 , takie że
, takie że
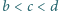 .
Udowodnić nierówność
.
Udowodnić nierówność
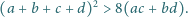
Dane jest słowo złożone z liter
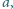
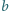 (np.
(np.
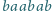 ). Na takim
słowie możemy wykonać następujące operacje:
). Na takim
słowie możemy wykonać następujące operacje:
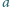 (np.
(np.
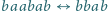 ),
),
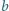 (np.
(np.
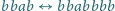 ),
),
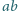 na
na
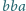 lub na odwrót
(np.
lub na odwrót
(np.
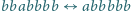 ).
).Rozstrzygnąć, czy za pomocą wielokrotnego wykonywania tych operacji można ze
słowa
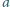 otrzymać słowo
otrzymać słowo
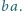
Zadanie zaproponował pan Witold Bednarek z Łodzi.
Niech
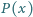 będzie wielomianem stopnia dodatniego o współczynnikach
całkowitych. Wykazać, że dla każdej liczby naturalnej
będzie wielomianem stopnia dodatniego o współczynnikach
całkowitych. Wykazać, że dla każdej liczby naturalnej
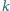 istnieje taka
liczba całkowita
istnieje taka
liczba całkowita
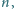 że liczba
że liczba
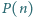 ma co najmniej
ma co najmniej
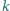 różnych dzielników pierwszych.
różnych dzielników pierwszych.
Dany jest wielomian
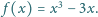 Definiujemy indukcyjnie
Definiujemy indukcyjnie
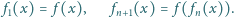
Dowieść, że wielomian
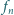 ma
ma
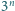 pierwiastków rzeczywistych.
pierwiastków rzeczywistych.