Kącik początkującego olimpijczyka
U(nie)jednorodnianie nierówności
Standardowym postępowaniem jest ujednorodnianie dowodzonych nierówności za pomocą danego w zadaniu warunku. Ciekawiej jest na odwrót - gdy mamy udowodnić jednorodną nierówność, możemy często założyć coś dodatkowo o występującej w niej zmiennych. Naprawdę!
W całym artykule stosujemy oznaczenia 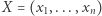 oraz
oraz
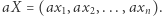 Będziemy pisać
Będziemy pisać 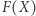 dla oznaczenia wyrażenia, w którym występują zmienne
dla oznaczenia wyrażenia, w którym występują zmienne 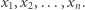 Zbiór
Zbiór 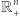 stanowią te
stanowią te 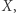 w których
w których 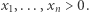
Stopniem jednomianu 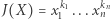 nazywamy liczbę
nazywamy liczbę 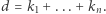 Równość
Równość 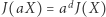 jest podstawą do uogólnienia pojęcia stopnia: jeśli istnieje takie
jest podstawą do uogólnienia pojęcia stopnia: jeśli istnieje takie 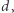 że dla każdego
że dla każdego 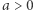 zachodzi równość
zachodzi równość 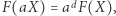 to wyrażenie
to wyrażenie 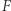 nazywamy jednorodnym, a liczbę
nazywamy jednorodnym, a liczbę 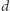 - jego stopniem. Zauważmy, że dla każdego
- jego stopniem. Zauważmy, że dla każdego 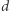 możemy powiedzieć, że wyrażenie zerowe ma stopień
możemy powiedzieć, że wyrażenie zerowe ma stopień 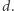
Nierówność 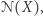 w której występują zmienne
w której występują zmienne 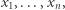 nazywamy jednorodną, jeśli obie jej strony są wyrażeniami jednorodnymi tego samego stopnia.
nazywamy jednorodną, jeśli obie jej strony są wyrażeniami jednorodnymi tego samego stopnia.
Załóżmy, że nierówność 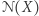 jest pod pewnym warunkiem
jest pod pewnym warunkiem 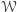 równoważna jednorodnej nierówności
równoważna jednorodnej nierówności 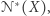 przy czym warunek
przy czym warunek 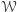 ma postać
ma postać 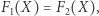 w której
w której 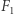 i
i 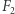 są jednorodnymi wyrażeniami różnych stopni, które przyjmują wyłącznie dodatnie wartości. Jest wówczas jasne, że jeśli
są jednorodnymi wyrażeniami różnych stopni, które przyjmują wyłącznie dodatnie wartości. Jest wówczas jasne, że jeśli 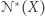 zachodzi dla wszystkich
zachodzi dla wszystkich 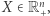 to
to 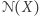 zachodzi dla wszystkich
zachodzi dla wszystkich 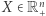 spełniających warunek
spełniających warunek 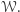
Takie postępowanie spotykamy dość często - za pomocą danego warunku 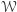 ujednorodniamy nierówność po to, by ją wykazać w postaci jednorodnej. Dzięki powyższemu twierdzeniu ten ostatni krok można wykonać już bez korzystania z warunku
ujednorodniamy nierówność po to, by ją wykazać w postaci jednorodnej. Dzięki powyższemu twierdzeniu ten ostatni krok można wykonać już bez korzystania z warunku 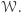 Taką metodą rozwiązujemy zadania 1-4, a także zadanie 5 z kącika nr 5.
Taką metodą rozwiązujemy zadania 1-4, a także zadanie 5 z kącika nr 5.
Mniej oczywiste i dość zaskakujące jest to, że ta implikacja działa również w drugą stronę: jeśli 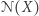 zachodzi dla wszystkich
zachodzi dla wszystkich 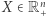 spełniających warunek
spełniających warunek 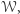 to
to 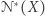 zachodzi dla wszystkich
zachodzi dla wszystkich 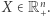
Dla dowodu ustalmy dowolne 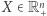 oraz połóżmy
oraz połóżmy 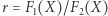 i
i 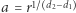 (
( 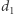 i
i 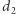 są stopniami odpowiednio
są stopniami odpowiednio 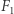 i
i 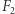 ). Otrzymujemy wtedy równości
). Otrzymujemy wtedy równości
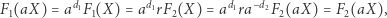 |
czyli zachodzi warunek 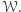 Z tego wynika, że nierówności
Z tego wynika, że nierówności 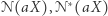 i
i 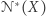 są równoważne, co kończy dowód wobec dowolności
są równoważne, co kończy dowód wobec dowolności 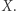
Konsekwencją tego faktu jest to, że przy dowodzeniu nierówności jednorodnej dodatnich zmiennych możemy dodatkowo przyjąć dowolny warunek 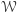 mający wyżej opisaną postać. Można to poćwiczyć na zadaniach 5-7.
mający wyżej opisaną postać. Można to poćwiczyć na zadaniach 5-7.