Kącik początkującego olimpijczyka
Lemat o zwiększaniu wykładnika p-adycznego
O zależnościach między  i
i 
W poprzednim kąciku omówiłem wykładnik 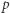 -adyczny
-adyczny  i jego podstawowe własności - zachęcam Czytelnika, aby się z nimi zapoznał przed przystąpieniem do lektury.
i jego podstawowe własności - zachęcam Czytelnika, aby się z nimi zapoznał przed przystąpieniem do lektury.
Weźmy dwie liczby całkowite 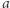 i
i 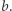 Niech
Niech  będzie liczbą pierwszą oraz
będzie liczbą pierwszą oraz 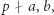 ale
ale  Możemy wówczas zapisać
Możemy wówczas zapisać 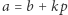 dla pewnego całkowitego
dla pewnego całkowitego  Zachodzi równość
Zachodzi równość
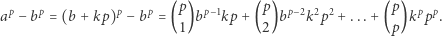 |
Zauważmy, że 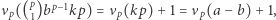 natomiast pozostałe składniki ostatniej sumy mają większe wykładniki
natomiast pozostałe składniki ostatniej sumy mają większe wykładniki  -adyczne. Na mocy własności (2') z poprzedniego kącika wynika z tego, że
-adyczne. Na mocy własności (2') z poprzedniego kącika wynika z tego, że 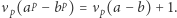
Niech teraz 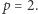 Interesują nas liczby nieparzyste
Interesują nas liczby nieparzyste 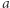 i
i 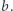 Zachodzi równość
Zachodzi równość 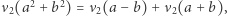 ale równość
ale równość  ma miejsce tylko wtedy, gdy
ma miejsce tylko wtedy, gdy 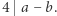
Trzymając się wciąż powyższych założeń, wybierzmy liczbę naturalną 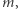 która nie jest podzielna przez
która nie jest podzielna przez  Wtedy
Wtedy
 |
więc w tym przypadku 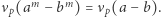
Stosując indukcję oraz powyższe rozważania, wykazujemy tytułowy lemat.
Lemat (o zwiększaniu wykładnika  -adycznego (wersja z odejmowaniem)). Niech
-adycznego (wersja z odejmowaniem)). Niech  i
i 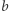 będą całkowite,
będą całkowite, 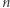 - naturalne,
- naturalne, 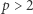 - pierwsze. Wówczas:
- pierwsze. Wówczas:
- (1)
- jeśli
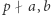 oraz
oraz 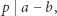 to
to 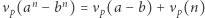 ;
; - (2)
- dla nieparzystych
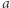 i
i 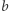 :
:
- (a)
- jeśli
 to
to 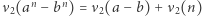 ;
; - (b)
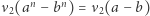 dla
dla 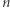 nieparzystych;
nieparzystych;- (c)
 dla
dla  parzystych.
parzystych.
Dla nieparzystego  zachodzi równość
zachodzi równość  Pisząc
Pisząc  zamiast
zamiast  otrzymamy analogiczny lemat dla dodawania.
otrzymamy analogiczny lemat dla dodawania.
Lemat (o zwiększaniu wykładnika 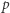 -adycznego (wersja z dodawaniem)). Niech
-adycznego (wersja z dodawaniem)). Niech 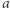 i
i 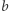 będą całkowite,
będą całkowite,  - naturalne nieparzyste,
- naturalne nieparzyste, 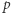 - pierwsze. Jeśli
- pierwsze. Jeśli 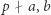 oraz
oraz 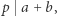 to
to 
W zadaniach dość powszechne jest stosowanie nierówności 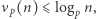 która być może jest oczywista, ale warto tu o niej wspomnieć.
która być może jest oczywista, ale warto tu o niej wspomnieć.