Kącik początkującego olimpijczyka
Wykładniki  -adyczne
-adyczne
O wygodnym narzędziu, przydatnym wszędzie tam, gdzie spotykamy rozkład na czynniki pierwsze
Niech 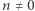 będzie liczbą całkowitą, zaś
będzie liczbą całkowitą, zaś 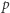 liczbą pierwszą. Wówczas największą taką liczbę całkowitą nieujemną
liczbą pierwszą. Wówczas największą taką liczbę całkowitą nieujemną 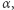 dla której
dla której 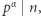 nazywamy wykładnikiem
nazywamy wykładnikiem 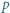 -adycznym liczby
-adycznym liczby 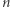 i oznaczamy
i oznaczamy 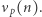 Dodatkowo przyjmujemy, że
Dodatkowo przyjmujemy, że 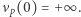
Dla 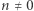 stwierdzenie
stwierdzenie 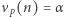 jest równoważne stwierdzeniu, że
jest równoważne stwierdzeniu, że 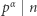 i
i 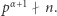 Stosuje się również notację
Stosuje się również notację 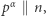 którą odczytujemy:
którą odczytujemy: 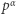 dzieli dokładnie
dzieli dokładnie 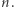 Możemy też zapisać
Możemy też zapisać 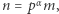 przy czym
przy czym 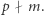 Warto jeszcze zauważyć, że
Warto jeszcze zauważyć, że 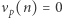 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 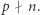
Wykładniki 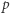 -adyczne mają następujące własności dla całkowitych
-adyczne mają następujące własności dla całkowitych 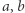 i dowolnej liczby pierwszej
i dowolnej liczby pierwszej 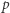 :
:
- (1)
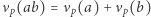 ; dla
; dla 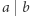 mamy
mamy 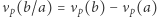 ;
;- (2)
- jeśli
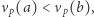 to
to 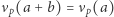 ;
; - (3)
- jeśli
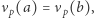 to
to 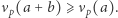
Dowód. Przypadek 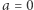 lub
lub 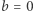 jest trywialny, więc go pominiemy. Niech
jest trywialny, więc go pominiemy. Niech 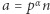 i
i 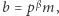 przy czym
przy czym 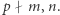 Równość
Równość 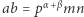 i niepodzielność
i niepodzielność 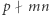 dowodzą pierwszej części własności (1). Druga część jasno wynika z pierwszej. Aby wykazać (2) i (3), zapiszmy
dowodzą pierwszej części własności (1). Druga część jasno wynika z pierwszej. Aby wykazać (2) i (3), zapiszmy 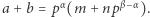 Korzystając z (1) mamy
Korzystając z (1) mamy 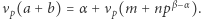 Jeśli
Jeśli 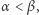 to
to 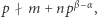 a jeśli
a jeśli 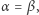 to liczba
to liczba 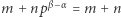 może, choć nie musi, być podzielna przez
może, choć nie musi, być podzielna przez 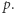
We własnościach (2) i (3) dodawanie można zastąpić odejmowaniem, dowód jest praktycznie taki sam. Indukcyjnie otrzymamy następujące uogólnienie na liczby całkowite 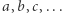 :
:
- (2')
- jeśli w ciągu
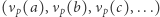 istnieje dokładnie jeden wyraz najmniejszy, to
istnieje dokładnie jeden wyraz najmniejszy, to 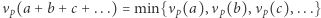 ;
; - (3')
- w każdym przypadku
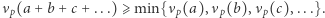
Posługując się twierdzeniem o jednoznaczności rozkładu na czynniki pierwsze, można wykazać, że dla liczb całkowitych dodatnich 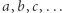 :
:
- (4)
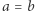 wtedy i tylko wtedy, gdy dla każdej liczby pierwszej
wtedy i tylko wtedy, gdy dla każdej liczby pierwszej 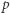 zachodzi równość
zachodzi równość 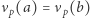 ;
;- (5)
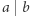 wtedy i tylko wtedy, gdy dla każdej liczby pierwszej
wtedy i tylko wtedy, gdy dla każdej liczby pierwszej 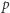 zachodzi nierówność
zachodzi nierówność 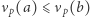 ;
;- (6)
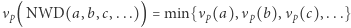 ;
;- (7)
![νp( NWW[a, b,c,...]) = max{ νp(a),νp(b),ν p(c),...}](/math/temat/matematyka/teoria_liczb/2020/10/31/wykladniki-p-adyczne/9x-d3840fec80f969e23a853676db6d3554607276bf-im-33,33,33-FF,FF,FF.gif) ;
;- (8)
- liczba
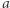 jest
jest 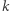 -tą potęgą liczby naturalnej wtedy i tylko wtedy, gdy dla każdej liczby pierwszej
-tą potęgą liczby naturalnej wtedy i tylko wtedy, gdy dla każdej liczby pierwszej 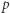 zachodzi podzielność
zachodzi podzielność 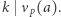
Dowód pozostawiamy Czytelnikowi.