Równoległobok to czworokąt, który ma dwie pary boków równoległych, ale można by go zdefiniować jeszcze na kilka innych sposobów. Dla czworokąta wypukłego 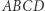następujące warunki są parami równoważne (dowód pomijamy):

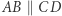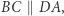
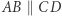• i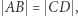
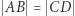• i
• i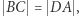
• odcink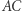i i 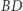mają wspólny środek.

Siła powyższego twierdzenia polega na tym, że jeśli wykażemy, że pewien czworokąt wypukły spełnia choć jeden z powyższych warunków, to możemy mieć pewność, że spełnia on wszystkie pozostałe.

Równoległoboki względnie często pojawiają się w zadaniach olimpijskich. Niekiedy jawnie - w założeniach lub tezie, gdy mamy dany pewien równoległobok lub chcemy wykazać, że jakiś czworokąt nim jest. Czasem treść zadania wskazuje na to, że gdzieś w rozważanej konfiguracji geometrycznej ukryty jest równoległobok, na przykład gdy trzeba wykazać, że jakaś prosta przechodzi przez środek jakiegoś odcinka. Nie brakuje również zadań, w których treści nie dopatrzymy się równoległoboku, ale musimy go znaleźć lub dorysować, aby zadanie rozwiązać.