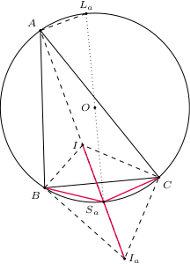
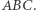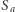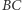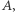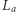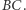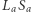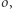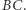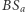Opiszmy okrąg na trójkącie Niech będzie środkiem łuku niezawierającego punktu zaś - środkiem drugiego łuku Odcinek jest oczywiście średnicą okręgu na której leży symetralna odcinka Łuki i 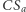są równej długości, więc kąty wpisane na nich oparte mają jednakową miarę, czyli prosta 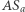jest dwusieczną kąta 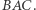Jeżeli 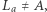to 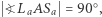więc prosta 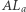jest dwusieczną kąta zewnętrznego 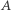trójkąta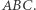

Oznaczmy przez 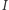środek okręgu wpisanego w trójkąt 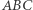oraz miary kątów wewnętrznych przy wierzchołkach 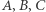odpowiednio przez 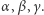Wówczas 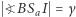oraz 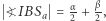więc 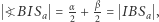co daje równość 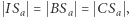znaną pod nazwą twierdzenie o trójliściu. Niech 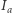będzie środkiem okręgu dopisanego do trójkąta 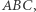stycznego do odcinka 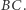Punkty 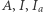leżą na jednej prostej, a ponadto 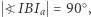więc 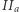jest średnicą okręgu opisanego na trójkącie 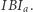To pozwala uzupełnić twierdzenie o trójliściu:

Nazywamy to twierdzeniem o trójzębie.