Potraktujmy zaczernione kwadraty jako wierzchołki skończonego grafu; para
wierzchołków jest połączona krawędzią grafu, gdy odpowiadające im kwadraty
sąsiadują (mają wspólny bok). Zgodnie z treścią zadania, z każdego
wierzchołka wychodzą dokładnie dwie krawędzie. Graf rozpada się zatem
na rozłączne cykle – to znany fakt (i łatwy do wykazania: z dowolnego
wierzchołka rozpoczynamy wędrówkę po krawędziach grafu, nie powtarzając
żadnej krawędzi; musimy wrócić do punktu wyjścia; odrzucamy
powstały cykl i powtarzamy postępowanie, do wyczerpania wszystkich
krawędzi).
Każdy cykl ma długość parzystą. Aby to zobaczyć, wystarczy sobie
wyobrazić, że (niezależnie od zaczernień rozważanych w zadaniu) cała
płaszczyzna jest „w tle” pomalowana dwoma odcieniami, jak szachownica,
a sąsiadujące kwadraty mają różne odcienie; zamknięcie cyklu wymaga
parzystej liczby kroków.
Tak więc liczba czarnych kwadratów jest parzysta. Jasne, że nie może ona
być równa 2 i że może być równa 4. Czy może być równa 6?
Musiałby to być pojedynczy cykl; znalazłby się w nim czarny kwadrat
narożny
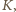 sąsiadujący np. od wschodu i od północy z dwoma
czarnymi kwadratami,
sąsiadujący np. od wschodu i od północy z dwoma
czarnymi kwadratami,
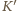 i
i
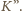 Kwadrat
Kwadrat
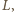 różny
od
różny
od
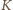 i sąsiadujący z
i sąsiadujący z
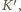
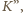 nie może być
zaczerniony (zamknąłby on cykl długości 4). Każda droga, łącząca
nie może być
zaczerniony (zamknąłby on cykl długości 4). Każda droga, łącząca
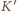 z
z
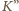 i omijająca kwadraty
i omijająca kwadraty
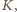
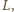 wymaga
zaczernienia więcej niż 3 kwadratów. Nie jest więc możliwe, by liczba
czarnych kwadratów wyniosła 6.
wymaga
zaczernienia więcej niż 3 kwadratów. Nie jest więc możliwe, by liczba
czarnych kwadratów wyniosła 6.
Może to być wszelako każda większa liczba parzysta
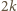
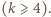 Wystarczy wziąć prostokąt o wymiarach
Wystarczy wziąć prostokąt o wymiarach
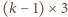 i zaczernić
wszystkie jego pola brzegowe. Jest ich dokładnie
i zaczernić
wszystkie jego pola brzegowe. Jest ich dokładnie
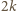 i tworzą cykl
o wymaganej własności.
i tworzą cykl
o wymaganej własności.
Dostajemy odpowiedź: liczba czarnych kwadratów może być dowolną dodatnią
liczbą parzystą z wyjątkiem 2 oraz 6.
 spełniające zależność
spełniające zależność
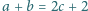 nie były tego samego
koloru?
nie były tego samego
koloru?
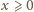 kolorujemy na kolor o numerze
kolorujemy na kolor o numerze
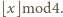 Załóżmy, że
Załóżmy, że
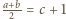 dla pewnych liczb
nieujemnych
dla pewnych liczb
nieujemnych
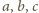 i przyjmijmy, że
i przyjmijmy, że
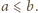 Załóżmy,
że
Załóżmy,
że
 i
i
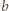 mają ten sam kolor. Niech
mają ten sam kolor. Niech
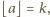 czyli
czyli
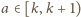 dla pewnej liczby całkowitej
dla pewnej liczby całkowitej
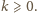 Wówczas
Wówczas
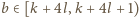 dla pewnej liczby całkowitej
dla pewnej liczby całkowitej
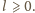 Zatem
Zatem
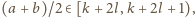 więc
więc
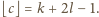 Ponieważ
Ponieważ
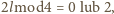 więc liczba
więc liczba
 ma w opisanym przez nas
kolorowaniu inny kolor niż liczby
ma w opisanym przez nas
kolorowaniu inny kolor niż liczby
 i
i
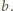
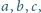 spełniające
spełniające
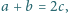 nie były tego samego koloru? Czy można pokolorować
w taki sposób zbiór liczb całkowitych nieujemnych?
nie były tego samego koloru? Czy można pokolorować
w taki sposób zbiór liczb całkowitych nieujemnych?
 jest
biała. Jedna z liczb
jest
biała. Jedna z liczb
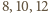 też musi być biała. Nazwijmy
ją
też musi być biała. Nazwijmy
ją
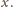 Wówczas liczby
Wówczas liczby
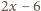 i
i
 muszą być czarne.
Zatem ich średnia
muszą być czarne.
Zatem ich średnia
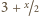 musi być biała. Dostaliśmy więc trzy białe
liczby
musi być biała. Dostaliśmy więc trzy białe
liczby
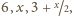 co daje sprzeczność.
co daje sprzeczność.
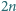 uczniów,
uczniów,
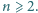 Każdego tygodnia
Każdego tygodnia
 uczniów dostaje bilety i jedzie na wycieczkę. Po
uczniów dostaje bilety i jedzie na wycieczkę. Po
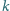 tygodniach
okazało się, że każdych dwóch uczniów było razem na przynajmniej jednej
wycieczce. Udowodnić, że
tygodniach
okazało się, że każdych dwóch uczniów było razem na przynajmniej jednej
wycieczce. Udowodnić, że
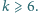
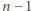 innymi uczniami, więc aby
spotkać się ze wszystkimi
innymi uczniami, więc aby
spotkać się ze wszystkimi
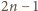 kolegami ze szkoły, musi wziąć udział
w przynajmniej
kolegami ze szkoły, musi wziąć udział
w przynajmniej
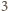 wycieczkach. Stąd liczba biletów wynosi co najmniej
wycieczkach. Stąd liczba biletów wynosi co najmniej
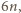 więc minęło co najmniej
więc minęło co najmniej
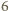 tygodni.
tygodni.
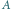
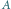
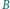
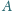 do
punktu
do
punktu
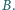 Którędy należy iść i ile jest różnych dróg do
wyboru?
Którędy należy iść i ile jest różnych dróg do
wyboru?
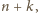 gdyż każda ma łącznie
gdyż każda ma łącznie
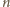 kratek na wschód i
kratek na wschód i
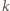 na
północ.
na
północ.
 znaków
znaków
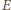 oraz
oraz
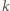 znaków
znaków
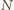 kodującym, czy na
kolejnym skrzyżowaniu należy iść na północ
kodującym, czy na
kolejnym skrzyżowaniu należy iść na północ
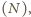 czy na
wschód
czy na
wschód
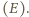 Najkrótszych dróg jest więc tyle, ile takich ciągów,
czyli
Najkrótszych dróg jest więc tyle, ile takich ciągów,
czyli
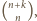 bo na tyle sposobów można wybrać, na których
bo na tyle sposobów można wybrać, na których
 spośród wszystkich
spośród wszystkich
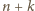 miejsc ciągu ma być znak
miejsc ciągu ma być znak
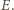
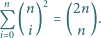
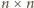 równa jest
równa jest
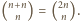
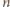 kolorowych punktów
kolorowych punktów
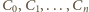 z
z 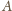 do
do
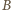 przechodzących przez
przechodzących przez
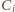 jest iloczynem liczby najkrótszych dróg z
jest iloczynem liczby najkrótszych dróg z
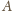 do
do
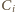 i liczby najkrótszych dróg z
i liczby najkrótszych dróg z
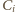 do
do
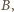 czyli –
z zadania 1 – równa jest
czyli –
z zadania 1 – równa jest
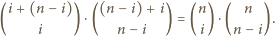
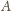 do
do
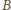 równa
jest
równa
jest
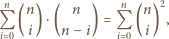
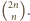
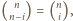 bo wybór
bo wybór
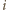 elementów z
elementów z
 równoważny jest odrzuceniu pozostałych
równoważny jest odrzuceniu pozostałych
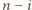 elementów.
elementów.
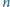 osób z banknotami 10
zł oraz
osób z banknotami 10
zł oraz
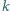 osób posiadających jedynie banknot 20 zł, przy czym
osób posiadających jedynie banknot 20 zł, przy czym
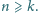 Jakie jest prawdopodobieństwo, że kasjerowi w trakcie obsługi
nie zabraknie reszty do wydawania?
Jakie jest prawdopodobieństwo, że kasjerowi w trakcie obsługi
nie zabraknie reszty do wydawania?

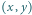

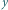
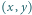

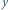
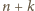 krokach: w danym kroku
idziemy w prawo, jeśli klient ma 10 zł, lub w górę, jeśli ma 20 zł. Aby
kasjerowi nie zabrakło reszty, liczba wręczonych mu banknotów 20 zł nigdy nie
może przekroczyć liczby banknotów 10 zł, które do tego momentu
dostał. Innymi słowy, droga jest dobra, jeśli nie dotyka kolorowej prostej
krokach: w danym kroku
idziemy w prawo, jeśli klient ma 10 zł, lub w górę, jeśli ma 20 zł. Aby
kasjerowi nie zabrakło reszty, liczba wręczonych mu banknotów 20 zł nigdy nie
może przekroczyć liczby banknotów 10 zł, które do tego momentu
dostał. Innymi słowy, droga jest dobra, jeśli nie dotyka kolorowej prostej
 z rysunku obok. Policzmy, ile jest złych dróg.
z rysunku obok. Policzmy, ile jest złych dróg.
 w punkcie
w punkcie
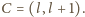 Jej część od punktu
Jej część od punktu
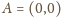 do punktu
do punktu
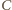 odbijmy symetrycznie względem prostej
odbijmy symetrycznie względem prostej
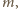 uzyskując
półodbicie złej drogi – nową drogę prowadzącą tylko w prawo lub w górę od
punktu
uzyskując
półodbicie złej drogi – nową drogę prowadzącą tylko w prawo lub w górę od
punktu
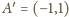 do punktu
do punktu
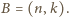 Każda zła droga
ma inne półodbicie. Ponadto każda najkrótsza droga z
Każda zła droga
ma inne półodbicie. Ponadto każda najkrótsza droga z
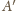 do
do
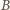 przecina prostą
przecina prostą
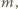 więc jest półodbiciem pewnej złej drogi.
Stąd złych dróg jest tyle, ile ich półodbić, czyli najkrótszych dróg
z
więc jest półodbiciem pewnej złej drogi.
Stąd złych dróg jest tyle, ile ich półodbić, czyli najkrótszych dróg
z
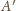 do
do
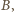 a więc, na mocy zadania 1,
a więc, na mocy zadania 1,
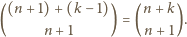
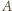 do
do
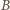 jest
jest
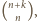 więc
liczba dobrych dróg to
więc
liczba dobrych dróg to
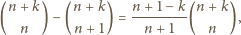
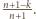
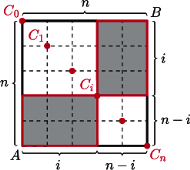
 zamalowano
zamalowano
 punktów. Udowodnić, że dla
pewnego
punktów. Udowodnić, że dla
pewnego
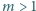 można wskazać
można wskazać
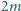 zamalowanych punktów
zamalowanych punktów
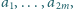 tak aby
tak aby
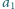 i
i
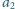 były w tym samym wierszu,
były w tym samym wierszu,
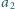 i
i
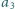 – w tej samej kolumnie,
– w tej samej kolumnie,
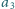 i
i
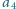 znów
w tym samym wierszu itd.,
znów
w tym samym wierszu itd.,
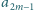 i
i
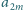 w tym samym
wierszu i wreszcie
w tym samym
wierszu i wreszcie
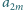 i
i
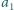 w tej samej kolumnie (tak jak na
w tej samej kolumnie (tak jak na
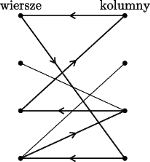
 będzie grafem o
będzie grafem o
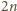 wierzchołkach oznaczających wiersze i
kolumny planszy. Krawędź pomiędzy wierszem
wierzchołkach oznaczających wiersze i
kolumny planszy. Krawędź pomiędzy wierszem
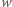 a kolumną
a kolumną
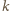 jest
w
jest
w
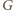 wtedy i tylko wtedy, gdy punkt o współrzędnych
wtedy i tylko wtedy, gdy punkt o współrzędnych
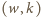 jest
zamalowany. Graf
jest
zamalowany. Graf
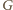 ma więc
ma więc
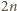 krawędzi. Jak wiadomo, jeśli graf
o
krawędzi. Jak wiadomo, jeśli graf
o
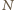 wierzchołkach nie ma cyklu, to ma co najwyżej
wierzchołkach nie ma cyklu, to ma co najwyżej
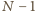 krawędzi. Zatem
krawędzi. Zatem
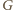 zawiera cykl. Z definicji krawędzi w
zawiera cykl. Z definicji krawędzi w
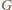 wynika,
że będzie on parzystej długości
wynika,
że będzie on parzystej długości
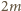 i wyznaczone przez niego krawędzie
to szukane punkty
i wyznaczone przez niego krawędzie
to szukane punkty
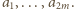
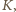 sąsiadujący np. od wschodu i od północy z dwoma
czarnymi kwadratami,
sąsiadujący np. od wschodu i od północy z dwoma
czarnymi kwadratami,
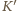 i
i
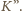 Kwadrat
Kwadrat
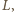 różny
od
różny
od
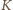 i sąsiadujący z
i sąsiadujący z
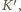
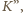 nie może być
zaczerniony (zamknąłby on cykl długości 4). Każda droga, łącząca
nie może być
zaczerniony (zamknąłby on cykl długości 4). Każda droga, łącząca
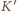 z
z
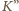 i omijająca kwadraty
i omijająca kwadraty
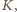
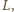 wymaga
zaczernienia więcej niż 3 kwadratów. Nie jest więc możliwe, by liczba
czarnych kwadratów wyniosła 6.
wymaga
zaczernienia więcej niż 3 kwadratów. Nie jest więc możliwe, by liczba
czarnych kwadratów wyniosła 6.
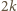
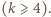 Wystarczy wziąć prostokąt o wymiarach
Wystarczy wziąć prostokąt o wymiarach
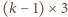 i zaczernić
wszystkie jego pola brzegowe. Jest ich dokładnie
i zaczernić
wszystkie jego pola brzegowe. Jest ich dokładnie
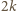 i tworzą cykl
o wymaganej własności.
i tworzą cykl
o wymaganej własności.
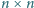 ma pola pokolorowane jak
szachownica;
ma pola pokolorowane jak
szachownica;
 jest ustaloną liczbą parzystą. Wykonujemy ciąg ruchów.
W każdym ruchu wybieramy dowolny prostokąt, złożony z pól planszy,
i zmieniamy kolory wszystkich pól w obrębie tego prostokąta (białe na czarne,
czarne na białe). Wyznaczyć najmniejszą liczbę ruchów wystarczającą, by
wszystkie pola planszy uzyskały jednakowy kolor.
jest ustaloną liczbą parzystą. Wykonujemy ciąg ruchów.
W każdym ruchu wybieramy dowolny prostokąt, złożony z pól planszy,
i zmieniamy kolory wszystkich pól w obrębie tego prostokąta (białe na czarne,
czarne na białe). Wyznaczyć najmniejszą liczbę ruchów wystarczającą, by
wszystkie pola planszy uzyskały jednakowy kolor.
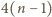 ; w stanie docelowym
wynosi 0. Jeden ruch może zmniejszyć liczbę takich par co najwyżej o 4.
Zatem liczba ruchów, po których plansza może stać się jednokolorowa, jest
nie mniejsza niż
; w stanie docelowym
wynosi 0. Jeden ruch może zmniejszyć liczbę takich par co najwyżej o 4.
Zatem liczba ruchów, po których plansza może stać się jednokolorowa, jest
nie mniejsza niż
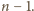
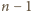 ruchów nie wystarczy do uzyskania żądanego celu, potrzeba co
najmniej
ruchów nie wystarczy do uzyskania żądanego celu, potrzeba co
najmniej
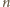 ruchów.
ruchów.
 ruchów faktycznie już wystarczy:
w początkowych
ruchów faktycznie już wystarczy:
w początkowych
 ruchach zmieniamy kolory w co drugim
wierszu, wszystkie kolumny stają się jednokolorowe (plansza „w zebrę”).
W kolejnych
ruchach zmieniamy kolory w co drugim
wierszu, wszystkie kolumny stają się jednokolorowe (plansza „w zebrę”).
W kolejnych
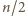 ruchach zmieniamy kolory w co drugiej kolumnie
i gotowe.
ruchach zmieniamy kolory w co drugiej kolumnie
i gotowe.
 -ty kamień?
-ty kamień?
 rycerzy. Wiadomo, że każdy rycerz ma
wśród pozostałych co najwyżej
rycerzy. Wiadomo, że każdy rycerz ma
wśród pozostałych co najwyżej
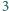 wrogów (zakładamy, że jeśli
rycerz
wrogów (zakładamy, że jeśli
rycerz
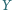 jest wrogiem rycerza
jest wrogiem rycerza
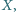 to i
to i
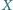 jest wrogiem
rycerza
jest wrogiem
rycerza
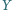 ). Udowodnić, że można tak rozsadzić rycerzy przy dwóch
stołach (dowolnie dużych), by każdy rycerz siedział przy stole z co najwyżej
jednym ze swoich wrogów.
). Udowodnić, że można tak rozsadzić rycerzy przy dwóch
stołach (dowolnie dużych), by każdy rycerz siedział przy stole z co najwyżej
jednym ze swoich wrogów.
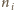 oznacza liczbę wrogów
oznacza liczbę wrogów
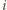 -tego rycerza, którzy zasiadają
z nim przy stole. W kroku 0 posadźmy wszystkich rycerzy przy pierwszym
stole. Będziemy w kolejnych krokach przesadzać rycerzy, rozważając
liczbę
-tego rycerza, którzy zasiadają
z nim przy stole. W kroku 0 posadźmy wszystkich rycerzy przy pierwszym
stole. Będziemy w kolejnych krokach przesadzać rycerzy, rozważając
liczbę
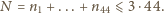
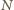 zmienia się na
zmienia się na
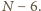 Jeśli zaś
siedział on przy stole wraz z dwoma wrogami, to
Jeśli zaś
siedział on przy stole wraz z dwoma wrogami, to
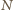 zmienia się na
liczbę niewiększą niż
zmienia się na
liczbę niewiększą niż
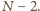 Skoro po wykonaniu każdego kroku
Skoro po wykonaniu każdego kroku
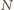 maleje, to wykonamy ich skończenie wiele. Oczywiście, po
wykonaniu ostatniego kroku
maleje, to wykonamy ich skończenie wiele. Oczywiście, po
wykonaniu ostatniego kroku
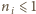 dla każdego
dla każdego
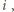 co kończy
dowód.
co kończy
dowód.
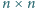 parami różnych liczb rzeczywistych.
Udowodnić, że można w niej zaznaczyć
parami różnych liczb rzeczywistych.
Udowodnić, że można w niej zaznaczyć
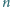 liczb, po jednej
w każdym wierszu i kolumnie, w taki sposób, że jeśli w pewnym wierszu
zaznaczona liczba jest większa od jakieś innej w tym wierszu, to ta druga liczba
jest mniejsza od zaznaczonej liczby z jej kolumny.
liczb, po jednej
w każdym wierszu i kolumnie, w taki sposób, że jeśli w pewnym wierszu
zaznaczona liczba jest większa od jakieś innej w tym wierszu, to ta druga liczba
jest mniejsza od zaznaczonej liczby z jej kolumny.
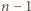 razy, więc
wykonamy co najwyżej
razy, więc
wykonamy co najwyżej
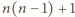 kroków. Po ostatnim kroku
w każdej kolumnie będzie zaznaczony dokładnie jeden element.
kroków. Po ostatnim kroku
w każdej kolumnie będzie zaznaczony dokładnie jeden element.
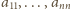 (możemy tak założyć, ewentualnie przestawiając
kolumny). Spójrzmy na
(możemy tak założyć, ewentualnie przestawiając
kolumny). Spójrzmy na
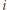 -ty wiersz. Jeśli
-ty wiersz. Jeśli
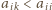 dla pewnego
dla pewnego
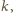 to znaczy, że w pewnym kroku liczba
to znaczy, że w pewnym kroku liczba
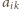 była odznaczona,
a zatem
była odznaczona,
a zatem
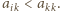
 -kąta foremnego są pokolorowane dwoma kolorami. Co
jednostkę czasu pokolorowanie zmienia się: każdy wierzchołek przyjmuje
kolor, który bezpośrednio przed tym momentem miała większość
z trójki wierzchołków: sam rozważany wierzchołek oraz dwa z nim
sąsiadujące. Proces kończy się, gdy nowe pokolorowanie okaże się identyczne
z poprzednim (tzn. gdy nic się już nie zmienia). Dla każdej liczby naturalnej
-kąta foremnego są pokolorowane dwoma kolorami. Co
jednostkę czasu pokolorowanie zmienia się: każdy wierzchołek przyjmuje
kolor, który bezpośrednio przed tym momentem miała większość
z trójki wierzchołków: sam rozważany wierzchołek oraz dwa z nim
sąsiadujące. Proces kończy się, gdy nowe pokolorowanie okaże się identyczne
z poprzednim (tzn. gdy nic się już nie zmienia). Dla każdej liczby naturalnej
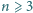 wyjaśnić, dla jakich początkowych konfiguracji kolorów proces
będzie trwał nieskończenie.
wyjaśnić, dla jakich początkowych konfiguracji kolorów proces
będzie trwał nieskończenie.
 parzystych). Wówczas po pierwszym ruchu
wszystkie kolory zmienią się, po drugim powróci sytuacja początkowa, i ten
cykl stale będzie się powtarzał. To jest ta konfiguracja początkowa, o jaką pyta
zadanie.
parzystych). Wówczas po pierwszym ruchu
wszystkie kolory zmienią się, po drugim powróci sytuacja początkowa, i ten
cykl stale będzie się powtarzał. To jest ta konfiguracja początkowa, o jaką pyta
zadanie.
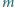 kolumn i
kolumn i
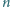 wierszy,
wpisujemy liczby
wierszy,
wpisujemy liczby
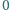 lub
lub
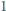 tak, by w każdym kwadracie
tak, by w każdym kwadracie
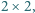 złożonym z czterech pól mających wspólny wierzchołek, suma
czterech wpisanych liczb była nieparzysta. Dla zadanej liczby naturalnej
złożonym z czterech pól mających wspólny wierzchołek, suma
czterech wpisanych liczb była nieparzysta. Dla zadanej liczby naturalnej
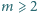 znaleźć wszystkie liczby naturalne
znaleźć wszystkie liczby naturalne
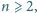 dla których da
się w taką tabelę wpisać zera i jedynki w opisany sposób tak, by żadne dwa
wiersze nie były identyczne.
dla których da
się w taką tabelę wpisać zera i jedynki w opisany sposób tak, by żadne dwa
wiersze nie były identyczne.
 Podany warunek (nieparzyste sumy w kwadratach
Podany warunek (nieparzyste sumy w kwadratach
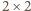 )
oznacza, że w dowolnych dwóch sąsiednich wierszach pola o numerach
parzystych są wypełnione jednakowo, a pola o numerach nieparzystych są
wypełnione różnie – lub że jest odwrotnie. Pomalujmy linię poziomą, która
te wiersze rozdziela, na szaro w pierwszym przypadku, a na żółto
w drugim.
)
oznacza, że w dowolnych dwóch sąsiednich wierszach pola o numerach
parzystych są wypełnione jednakowo, a pola o numerach nieparzystych są
wypełnione różnie – lub że jest odwrotnie. Pomalujmy linię poziomą, która
te wiersze rozdziela, na szaro w pierwszym przypadku, a na żółto
w drugim.
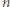 wierszy parami różnych,
wierszy parami różnych,
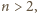 to jednakowo pomalowane linie nie mogą sąsiadować. Linie szare
i żółte występują wówczas na przemian, więc każde dwa wiersze
o numerach różniących się o 2 są wypełnione dokładnie przeciwnie
(w kolumnach, gdzie górny ma zera, dolny ma jedynki, i na odwrót).
Wobec tego wiersze o numerach różniących się o 4 są już wypełnione
identycznie.
to jednakowo pomalowane linie nie mogą sąsiadować. Linie szare
i żółte występują wówczas na przemian, więc każde dwa wiersze
o numerach różniących się o 2 są wypełnione dokładnie przeciwnie
(w kolumnach, gdzie górny ma zera, dolny ma jedynki, i na odwrót).
Wobec tego wiersze o numerach różniących się o 4 są już wypełnione
identycznie.
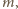 maksymalna liczba parami nieidentycznych
wierszy nie przekracza 4. Przy tym łatwo wskazać przykład takiej macierzy
z dokładnie 4 wierszami:
maksymalna liczba parami nieidentycznych
wierszy nie przekracza 4. Przy tym łatwo wskazać przykład takiej macierzy
z dokładnie 4 wierszami:
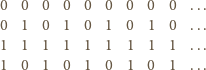
 o które pyta zadanie – to 2, 3, 4.
o które pyta zadanie – to 2, 3, 4.
 Za prawidłową
odpowiedź na
Za prawidłową
odpowiedź na
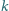 -te pytanie uczestnik otrzymuje
-te pytanie uczestnik otrzymuje
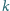 punktów; za
błędną (lub brak odpowiedzi) otrzymuje
punktów; za
błędną (lub brak odpowiedzi) otrzymuje
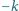 punktów. Po zliczeniu
wyników okazało się, że w każdej trójce uczestników znajdują się dwaj
tacy, którzy uzyskali różne sumy punktów. Jaka jest największa liczba
uczestników, dla której taka sytuacja mogła mieć miejsce?
punktów. Po zliczeniu
wyników okazało się, że w każdej trójce uczestników znajdują się dwaj
tacy, którzy uzyskali różne sumy punktów. Jaka jest największa liczba
uczestników, dla której taka sytuacja mogła mieć miejsce?
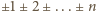 (dowolny układ znaków). Wszystkie takie liczby są jednakowej parzystości.
Zatem zbiór możliwych wyników zawiera się w zbiorze
(dowolny układ znaków). Wszystkie takie liczby są jednakowej parzystości.
Zatem zbiór możliwych wyników zawiera się w zbiorze
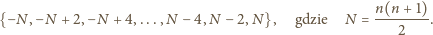
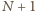 elementów. Wykażemy, że każdy
element jest możliwym wynikiem.
elementów. Wykażemy, że każdy
element jest możliwym wynikiem.
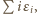 gdzie
gdzie
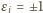 i nie wszystkie
i nie wszystkie
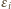 są równe
są równe
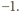 Zamieniamy ciąg
Zamieniamy ciąg
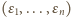 na ciąg
na ciąg
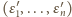 określony następująco:
określony następująco:
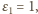 bierzemy
bierzemy
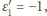 pozostałe
pozostałe
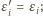
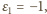 znajdujemy najmniejszy
numer
znajdujemy najmniejszy
numer
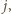 dla którego
dla którego
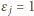 (więc
(więc
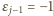 );
przyjmujemy
);
przyjmujemy
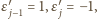 pozostałe
pozostałe
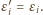
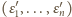 ma wynik
ma wynik
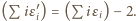 Startując od prymusa z wektorem
Startując od prymusa z wektorem
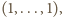 czyli
z wynikiem
czyli
z wynikiem
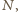 możemy w opisany sposób wygenerować
kolejno wyniki
możemy w opisany sposób wygenerować
kolejno wyniki
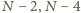 itd., aż do
itd., aż do
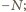 łącznie
łącznie
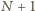 wyników.
wyników.
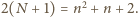
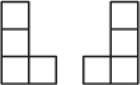
 dla których kwadrat
złożony z
dla których kwadrat
złożony z
 kwadracików jednostkowych można pokryć
płytkami powstałymi z płytek pokazanych na rysunku przez obrót o kąt
kwadracików jednostkowych można pokryć
płytkami powstałymi z płytek pokazanych na rysunku przez obrót o kąt
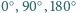 lub
lub
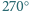 w ten sposób, by płytki nie zachodziły na
siebie.
w ten sposób, by płytki nie zachodziły na
siebie.

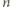 jest podzielne
przez
jest podzielne
przez
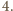
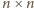 udało się pokryć dostępnymi płytkami.
Skoro pole płytki wynosi
udało się pokryć dostępnymi płytkami.
Skoro pole płytki wynosi
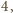 to
to
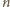 musi być parzyste, powiedzmy
musi być parzyste, powiedzmy
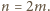 Rozważmy kolorowanie naszego kwadratu w pasy jak na rysunku.
Zauważmy, że każda płytka jest jednego z dwóch rodzajów: zawiera
Rozważmy kolorowanie naszego kwadratu w pasy jak na rysunku.
Zauważmy, że każda płytka jest jednego z dwóch rodzajów: zawiera
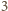 czarne pola lub
czarne pola lub
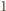 czarne pole. Niech liczba płytek pierwszego
rodzaju wynosi
czarne pole. Niech liczba płytek pierwszego
rodzaju wynosi
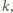 a drugiego
a drugiego
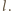 Zliczając czarne i białe pola,
otrzymujemy
Zliczając czarne i białe pola,
otrzymujemy
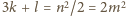 oraz
oraz
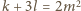 (dzięki temu,
że
(dzięki temu,
że
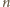 jest parzyste, mamy po równo pól czarnych i białych!). Stąd
w szczególności
jest parzyste, mamy po równo pól czarnych i białych!). Stąd
w szczególności
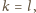 więc
więc
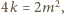 zatem
zatem
 jest
parzyste, a
jest
parzyste, a
 – podzielne przez
– podzielne przez
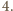
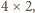 zatem
łatwo można znaleźć pokrycie kwadratu
zatem
łatwo można znaleźć pokrycie kwadratu
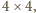 więc także
dowolnego kwadratu
więc także
dowolnego kwadratu
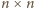 dla
dla
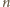 będącego wielokrotnością
będącego wielokrotnością
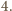
 oraz
oraz
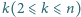 . Wyznaczyć
maksymalną liczbę wież, które można ustawić na szachownicy o rozmiarach
. Wyznaczyć
maksymalną liczbę wież, które można ustawić na szachownicy o rozmiarach
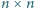 tak, by wśród dowolnie wybranych
tak, by wśród dowolnie wybranych
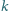 wież były dwie,
które się wzajemnie atakują (przyjmujemy, że atakują się wzajemnie każde
dwie wieże, stojące w tym samym rzędzie poziomym lub pionowym,
niezależnie od tego, czy są pomiędzy nimi jeszcze jakieś inne wieże).
wież były dwie,
które się wzajemnie atakują (przyjmujemy, że atakują się wzajemnie każde
dwie wieże, stojące w tym samym rzędzie poziomym lub pionowym,
niezależnie od tego, czy są pomiędzy nimi jeszcze jakieś inne wieże).
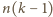 wież w żądany sposób; wystarczy
zapełnić nimi prostokąt
wież w żądany sposób; wystarczy
zapełnić nimi prostokąt
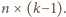 Pokażemy, że więcej się nie
da.
Pokażemy, że więcej się nie
da.
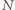 wież. Niech
wież. Niech
 będzie
największą liczbą wież, jakie można wybrać spośród nich, by żadne dwie
się nie atakowały. Należy dowieść, że jeśli
będzie
największą liczbą wież, jakie można wybrać spośród nich, by żadne dwie
się nie atakowały. Należy dowieść, że jeśli
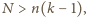 to
to
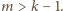 Wystarczy wykazać, że
Wystarczy wykazać, że
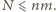
 wież, z których żadne dwie nie stoją w jednym
wierszu ani jednej kolumnie. Permutując wiersze i kolumny, można przyjąć,
że te wieże stoją na polach
wież, z których żadne dwie nie stoją w jednym
wierszu ani jednej kolumnie. Permutując wiersze i kolumny, można przyjąć,
że te wieże stoją na polach
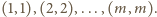 Podzielmy
szachownicę na cztery obszary
Podzielmy
szachownicę na cztery obszary
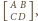 gdzie
gdzie
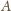 jest kwadratem
jest kwadratem
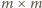 (na jego przekątnej stoją wybrane wieże),
(na jego przekątnej stoją wybrane wieże),
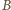 i
i
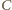 to
prostokąty
to
prostokąty
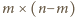 oraz
oraz
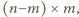 zaś
zaś
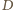 to kwadrat
to kwadrat
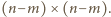 Wobec maksymalności
Wobec maksymalności
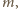 żadna wieża nie
znajduje się w obrębie kwadratu
żadna wieża nie
znajduje się w obrębie kwadratu
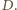
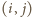 w prostokącie
w prostokącie
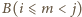 i symetryczne
do niego pole
i symetryczne
do niego pole
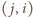 w prostokącie
w prostokącie
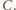 Gdyby na obu tych polach
stały wieże, to usuwając z poprzednio ustalonego układu wieżę z pola
Gdyby na obu tych polach
stały wieże, to usuwając z poprzednio ustalonego układu wieżę z pola
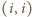 oraz dołączając wieże z pól
oraz dołączając wieże z pól
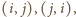 otrzymalibyśmy
układ
otrzymalibyśmy
układ
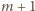 wież, stojących w różnych wierszach i kolumnach
– wbrew maksymalności
wież, stojących w różnych wierszach i kolumnach
– wbrew maksymalności
 Zatem co najwyżej połowa pól
w sumie prostokątów
Zatem co najwyżej połowa pól
w sumie prostokątów
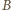 i
i
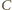 jest zajęta, czyli nie więcej
niż
jest zajęta, czyli nie więcej
niż
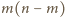 pól. Uwzględniając
pól. Uwzględniając
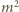 pól kwadratu
pól kwadratu
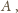 uzyskujemy oczekiwane oszacowanie:
uzyskujemy oczekiwane oszacowanie:
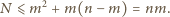

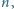 dla których kwadrat
złożony z
dla których kwadrat
złożony z
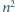 kwadracików jednostkowych można pokryć
płytkami powstałymi z płytki pokazanej na rysunku przez obrót o kąt
kwadracików jednostkowych można pokryć
płytkami powstałymi z płytki pokazanej na rysunku przez obrót o kąt
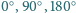 lub
lub
 w ten sposób, by płytki nie zachodziły na
siebie.
w ten sposób, by płytki nie zachodziły na
siebie.

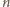 jest
podzielne przez
jest
podzielne przez
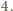
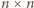 udało się
pokryć dostępnymi płytkami. Skoro pole płytki wynosi
udało się
pokryć dostępnymi płytkami. Skoro pole płytki wynosi
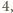 to
to
 musi być parzyste, powiedzmy
musi być parzyste, powiedzmy
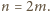 Rozważmy
kolorowanie naszego kwadratu jak standardowej szachownicy i zauważmy, że
każda płytka jest jednego z dwóch rodzajów: zawiera
Rozważmy
kolorowanie naszego kwadratu jak standardowej szachownicy i zauważmy, że
każda płytka jest jednego z dwóch rodzajów: zawiera
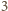 czarne pola
lub
czarne pola
lub
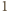 czarne pole. Niech liczba płytek pierwszego rodzaju wynosi
czarne pole. Niech liczba płytek pierwszego rodzaju wynosi
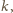 a drugiego
a drugiego
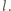 Zliczając czarne i białe pola, otrzymujemy
Zliczając czarne i białe pola, otrzymujemy
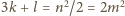 oraz
oraz
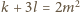 (dzięki temu, że
(dzięki temu, że
 jest parzyste, mamy po równo pól czarnych i białych!). Stąd
w szczególności
jest parzyste, mamy po równo pól czarnych i białych!). Stąd
w szczególności
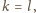 więc
więc
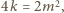 zatem
zatem
 jest
parzyste, a
jest
parzyste, a
 – podzielne przez
– podzielne przez
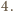
 spełniające
warunki zadania, więc także dowolnego kwadratu
spełniające
warunki zadania, więc także dowolnego kwadratu
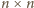 dla
dla
 będącego wielokrotnością
będącego wielokrotnością
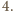
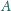 zna osobę
zna osobę
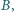 to także osoba
to także osoba
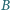 zna osobę
zna osobę
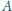 ).
).
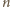 liczbę osób w rozważanej grupie. Wówczas każda
z nich może znać
liczbę osób w rozważanej grupie. Wówczas każda
z nich może znać
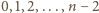 lub wszystkich
lub wszystkich
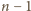 spośród
pozostałych; łącznie jest
spośród
pozostałych; łącznie jest
 możliwości – tyle, ile osób. Gdyby
każdy miał inną liczbę znajomych, to w rozważanym gronie byłaby
osoba
możliwości – tyle, ile osób. Gdyby
każdy miał inną liczbę znajomych, to w rozważanym gronie byłaby
osoba
 która nie zna nikogo, oraz osoba
która nie zna nikogo, oraz osoba
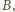 która zna
wszystkich. To prowadzi do sprzeczności, bo czy wtedy
która zna
wszystkich. To prowadzi do sprzeczności, bo czy wtedy
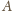 i
i
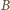 się
znają, czy nie? Wobec tego nie jest możliwe, by każdy miał inną liczbę
znajomych.
się
znają, czy nie? Wobec tego nie jest możliwe, by każdy miał inną liczbę
znajomych.

 pomalowane jest na biało lub czarno.
W jednym ruchu możemy w dowolnej podszachownicy wymiaru
pomalowane jest na biało lub czarno.
W jednym ruchu możemy w dowolnej podszachownicy wymiaru
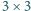 lub
lub
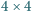 zamienić kolory na przeciwne. Czy dla dowolnego początkowego
pokolorowania istnieje sekwencja ruchów dająca w efekcie całą białą
szachownicę?
zamienić kolory na przeciwne. Czy dla dowolnego początkowego
pokolorowania istnieje sekwencja ruchów dająca w efekcie całą białą
szachownicę?
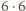 podszachownic wymiaru
podszachownic wymiaru
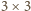 i
i
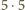 podszachownic wymiaru
podszachownic wymiaru
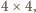 to istnieje
to istnieje
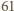 pojedynczych
ruchów możliwych do wykonania. Zauważmy, że wykonanie ruchu
pojedynczych
ruchów możliwych do wykonania. Zauważmy, że wykonanie ruchu
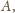 a następnie ruchu
a następnie ruchu
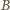 prowadzi do tego samego kolorowania
szachownicy, co wykonanie najpierw ruchu
prowadzi do tego samego kolorowania
szachownicy, co wykonanie najpierw ruchu
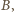 a potem ruchu
a potem ruchu
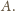 Ponadto wykonanie tego samego ruchu parzystą liczbę razy nie zmienia
kolorowania szachownicy. Zatem każda sekwencja ruchów jest jednoznacznie
opisana przez podanie ruchów występujących w niej nieparzystą liczbę razy. Jest
więc nie więcej niż
Ponadto wykonanie tego samego ruchu parzystą liczbę razy nie zmienia
kolorowania szachownicy. Zatem każda sekwencja ruchów jest jednoznacznie
opisana przez podanie ruchów występujących w niej nieparzystą liczbę razy. Jest
więc nie więcej niż
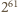 nierównoważnych sekwencji ruchów
(sekwencje uznajemy za równoważne, jeśli dają ten sam efekt). Startując
z ustalonego kolorowania szachownicy, otrzymamy zatem co najwyżej
nierównoważnych sekwencji ruchów
(sekwencje uznajemy za równoważne, jeśli dają ten sam efekt). Startując
z ustalonego kolorowania szachownicy, otrzymamy zatem co najwyżej
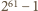 innych kolorowań. Ale wszystkich możliwych pokolorowań
szachownicy jest
innych kolorowań. Ale wszystkich możliwych pokolorowań
szachownicy jest
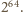 Znajdzie się więc takie, którego nie otrzymamy
żadną sekwencją ruchów z całej białej szachownicy. Równoważnie, znajdzie
się takie pokolorowanie, którego żadną sekwencją ruchów nie sprowadzimy
do całej białej szachownicy.
Znajdzie się więc takie, którego nie otrzymamy
żadną sekwencją ruchów z całej białej szachownicy. Równoważnie, znajdzie
się takie pokolorowanie, którego żadną sekwencją ruchów nie sprowadzimy
do całej białej szachownicy.
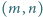 liczb całkowitych
liczb całkowitych
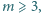
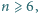 spełniające równanie
spełniające równanie

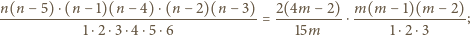
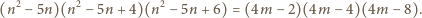
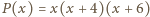 i przepisujemy
równanie jako
i przepisujemy
równanie jako
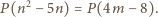
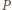 jest funkcją rosnącą; stąd
równoważne równanie
jest funkcją rosnącą; stąd
równoważne równanie
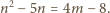
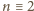 lub
lub
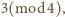 lewa strona ostatniego równania nie dzieli się
przez 4; brak rozwiązań. Natomiast każda liczba
lewa strona ostatniego równania nie dzieli się
przez 4; brak rozwiązań. Natomiast każda liczba
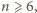 spełniająca warunek
spełniająca warunek
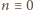 lub
lub
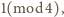 wraz z liczbą
wraz z liczbą
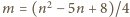 daje
parę, spełniającą ostatnie równanie – więc i równoważne mu równanie
wyjściowe.
daje
parę, spełniającą ostatnie równanie – więc i równoważne mu równanie
wyjściowe.
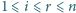 będą liczbami naturalnymi. Rozważmy
będą liczbami naturalnymi. Rozważmy
 -elementowe podzbiory zbioru
-elementowe podzbiory zbioru
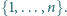 Dla takiego podzbioru
niech
Dla takiego podzbioru
niech
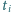 oznacza jego
oznacza jego
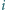 -ty element, przy założeniu, że elementy są
uporządkowane malejąco. Udowodnić, że średnia arytmetyczna wszystkich
tak uzyskanych liczb
-ty element, przy założeniu, że elementy są
uporządkowane malejąco. Udowodnić, że średnia arytmetyczna wszystkich
tak uzyskanych liczb
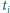 wynosi
wynosi
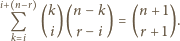
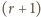 -elementowe podzbiory
zbioru
-elementowe podzbiory
zbioru
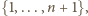 dla których
dla których
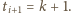 Wtedy
Wtedy
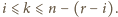 Zatem elementy
Zatem elementy
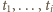 i
i
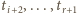 możemy wybrać na
możemy wybrać na
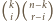 sposobów. Sumując
te możliwości po dozwolonych wartościach
sposobów. Sumując
te możliwości po dozwolonych wartościach
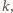 dostajemy żądany
wzór.
dostajemy żądany
wzór.
 -elementowe podzbiory zbioru
-elementowe podzbiory zbioru
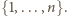 Takich
podzbiorów, dla których
Takich
podzbiorów, dla których
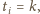 jest
jest
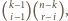 gdzie
gdzie
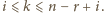 Zatem średnia arytmetyczna liczb
Zatem średnia arytmetyczna liczb
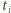 wynosi
wynosi
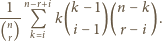
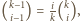 więc ta średnia jest równa
więc ta średnia jest równa
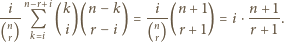
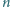 pytań (
pytań (
 ). Pewna liczba studentów
przystąpiła do tego egzaminu. Wiadomo, że dla każdych dwóch studentów
było przynajmniej jedno pytanie, na które obaj znali odpowiedź, ale dla
żadnej pary studentów nie było tak, że obaj znali odpowiedzi na dokładnie
te same pytania. Udowodnić, że do egzaminu przystąpiło co najwyżej
). Pewna liczba studentów
przystąpiła do tego egzaminu. Wiadomo, że dla każdych dwóch studentów
było przynajmniej jedno pytanie, na które obaj znali odpowiedź, ale dla
żadnej pary studentów nie było tak, że obaj znali odpowiedzi na dokładnie
te same pytania. Udowodnić, że do egzaminu przystąpiło co najwyżej
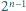 studentów.
studentów.
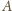 zbioru
zbioru
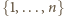 łączymy w nieuporządkowane pary
postaci
łączymy w nieuporządkowane pary
postaci
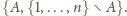 Takich par jest
Takich par jest
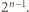 Wobec założenia
z treści zadania każdego studenta możemy utożsamiać jednoznacznie ze
zbiorem pytań, na które zna odpowiedź. Gdyby studentów było więcej niż
Wobec założenia
z treści zadania każdego studenta możemy utożsamiać jednoznacznie ze
zbiorem pytań, na które zna odpowiedź. Gdyby studentów było więcej niż
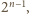 to znalazłoby się dwóch, którym odpowiadałyby zbiory
to znalazłoby się dwóch, którym odpowiadałyby zbiory
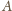 i
i
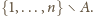 To jednak przeczyłoby założeniu, że na egzaminie było
pytanie, na które obaj znali odpowiedź.
To jednak przeczyłoby założeniu, że na egzaminie było
pytanie, na które obaj znali odpowiedź.
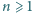 zachodzą następujące
równości:
zachodzą następujące
równości:
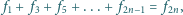
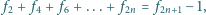
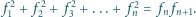
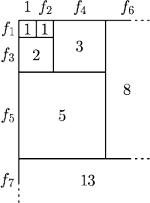
 – następny kwadrat „pasuje” do
dwóch poprzednich.
– następny kwadrat „pasuje” do
dwóch poprzednich.
 to cały prostokąt
ma taką właśnie szerokość, a wysokość równą następnemu
wyrazowi ciągu, czyli
to cały prostokąt
ma taką właśnie szerokość, a wysokość równą następnemu
wyrazowi ciągu, czyli
 Jednocześnie wysokość ta jest
równa
Jednocześnie wysokość ta jest
równa

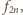 to prostokąt ma szerokość
równą
to prostokąt ma szerokość
równą
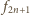 i zarazem równą
i zarazem równą
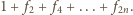
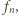 to
prostokąt
ma taką właśnie szerokość lub wysokość, a drugi z wymiarów
równy
to
prostokąt
ma taką właśnie szerokość lub wysokość, a drugi z wymiarów
równy
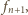 więc ma pole
więc ma pole
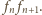 Jednocześnie pole to
jest równe
Jednocześnie pole to
jest równe
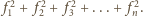
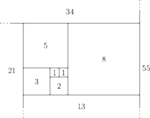
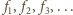 kolejno po prawej, na dole, po lewej,
na górze, znów po prawej itd., jak na
kolejno po prawej, na dole, po lewej,
na górze, znów po prawej itd., jak na  i szerokości 1, mając do dyspozycji duży zapas płyt o rozmiarach
i szerokości 1, mając do dyspozycji duży zapas płyt o rozmiarach
 oraz
oraz
 ?
?
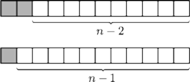
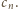 Dla
Dla
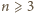 na początku
chodnika możemy położyć płytę
na początku
chodnika możemy położyć płytę
 a następnie na
a następnie na
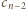 sposobów ułożyć resztę (chodnik o długości
sposobów ułożyć resztę (chodnik o długości
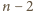 );
możemy też zacząć od płyty
);
możemy też zacząć od płyty
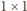 i wtedy na
i wtedy na
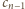 sposobów
ułożyć resztę. Stąd
sposobów
ułożyć resztę. Stąd
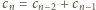 dla
dla
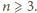 Otrzymany
wzór jest taki sam, jak dla ciągu Fibonacciego. Nietrudno sprawdzić, że
Otrzymany
wzór jest taki sam, jak dla ciągu Fibonacciego. Nietrudno sprawdzić, że
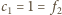 oraz
oraz
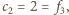 uzyskujemy więc wniosek, że
uzyskujemy więc wniosek, że
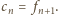

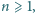
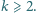
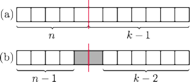
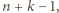 takich jak opisano
w poprzednim zadaniu, można rozciąć na chodnik o długości
takich jak opisano
w poprzednim zadaniu, można rozciąć na chodnik o długości
 (od
lewej strony) oraz chodnik o długości
(od
lewej strony) oraz chodnik o długości
 (po prawej stronie) bez
rozcinania poszczególnych płyt (
(po prawej stronie) bez
rozcinania poszczególnych płyt (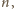 a po prawej chodnik długości
a po prawej chodnik długości
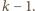 Z poprzedniego
zadania wiemy, że możliwości tych jest po lewej
Z poprzedniego
zadania wiemy, że możliwości tych jest po lewej
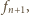 po prawej
po prawej
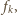 więc łącznie
więc łącznie
 Cięcie chodnika wymaga rozcinania płyty,
gdy w miejscu podziału leży płyta
Cięcie chodnika wymaga rozcinania płyty,
gdy w miejscu podziału leży płyta
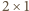 (
(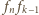 : układamy od lewej kolejno chodnik
długości
: układamy od lewej kolejno chodnik
długości
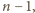 następnie płytę
następnie płytę
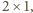 a po prawej chodnik
długości
a po prawej chodnik
długości
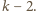 Wszystkich chodników, jak wiemy z poprzedniego
zadania, jest
Wszystkich chodników, jak wiemy z poprzedniego
zadania, jest
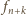 i każdy z nich da się rozciąć w opisany sposób
lub nie, stąd
i każdy z nich da się rozciąć w opisany sposób
lub nie, stąd


 na
serwetce, pokazane na rysunku (b). Zgodnie z treścią zadania nie można
zamalować trzech pól z tą samą literą, więc można zamalować co najwyżej
na
serwetce, pokazane na rysunku (b). Zgodnie z treścią zadania nie można
zamalować trzech pól z tą samą literą, więc można zamalować co najwyżej
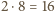 pól.
pól.