Klub 44M - zadania IV 2019»Zadanie 779
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania IV 2019
- Publikacja w Delcie: kwiecień 2019
- Publikacja elektroniczna: 31 marca 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (293 KB)
W pola planszy kwadratowej wpisujemy liczby całkowite (w każde pole jedną liczbę) tak, by liczby wpisane w dowolne dwa przyległe pola były równe lub różniły się o 1 (pola przyległe mają wspólny bok). Dla ustalonej liczby naturalnej 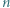 wyznaczyć największą liczbę
wyznaczyć największą liczbę 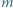 taką, że przy każdym wypełnieniu planszy
taką, że przy każdym wypełnieniu planszy 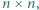 zgodnym z podanym warunkiem, pewna liczba pojawia się na co najmniej
zgodnym z podanym warunkiem, pewna liczba pojawia się na co najmniej 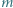 polach planszy.
polach planszy.

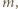 o jakiej mowa, to
o jakiej mowa, to 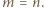 Macierz
Macierz ![|[ai j]](/math/temat/matematyka/kombinatoryka/zadania/2019/03/31/zm-k44-779/3x-0ea823dd3c43a983e9f06ad8aefabe5d4b92bbfe-im-66,57,43-FF,FF,FF.gif) o wyrazach
o wyrazach 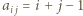
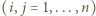 daje przykład wypełnienia planszy, przy którym liczba
daje przykład wypełnienia planszy, przy którym liczba 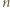 pojawia się
pojawia się  razy (cała jedna przekątna), a żadna liczba nie występuje więcej niż
razy (cała jedna przekątna), a żadna liczba nie występuje więcej niż 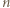 razy. Pozostaje wykazać, że przy każdym wypełnieniu planszy, zgodnym z podanym warunkiem, pewna liczba wystąpi
razy. Pozostaje wykazać, że przy każdym wypełnieniu planszy, zgodnym z podanym warunkiem, pewna liczba wystąpi 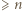 razy.
razy.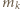 oraz
oraz 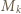 oznaczają najmniejszą oraz największą liczbę w kolumnie
oznaczają najmniejszą oraz największą liczbę w kolumnie 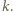 Liczby w sąsiednich polach różnią się co najwyżej o 1, więc w
Liczby w sąsiednich polach różnią się co najwyżej o 1, więc w 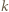 -tej kolumnie są wszystkie liczby całkowite z przedziału
-tej kolumnie są wszystkie liczby całkowite z przedziału ![k]. [mk,](/math/temat/matematyka/kombinatoryka/zadania/2019/03/31/zm-k44-779/5x-3851dd7da0ebfd80395100c363b83f096c5c4a58-im-66,57,43-FF,FF,FF.gif)
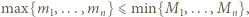 wówczas pewna liczba całkowita należy do wszystkich przedziałów
wówczas pewna liczba całkowita należy do wszystkich przedziałów ![1],...,[mn,Mn]. [m1,](/math/temat/matematyka/kombinatoryka/zadania/2019/03/31/zm-k44-779/2x-a07165ea6eadac3996e30bccf992e2921733620d-im-66,57,43-FF,FF,FF.gif) Jest ona obecna we wszystkich kolumnach, więc występuje
Jest ona obecna we wszystkich kolumnach, więc występuje 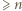 -krotnie na planszy.
-krotnie na planszy.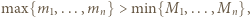 znaczy to, że dla pewnych numerów kolumn
znaczy to, że dla pewnych numerów kolumn 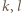 zachodzi nierówność
zachodzi nierówność 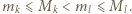 Weźmy dowolny wiersz. Na przecięciu z kolumnami
Weźmy dowolny wiersz. Na przecięciu z kolumnami 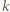 i
i 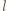 są w tym wierszu: pewna liczba
są w tym wierszu: pewna liczba 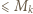 oraz pewna liczba
oraz pewna liczba 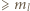 ; zatem są w tym wierszu wszystkie liczby całkowite z przedziału
; zatem są w tym wierszu wszystkie liczby całkowite z przedziału ![,m]. [M kl](/math/temat/matematyka/kombinatoryka/zadania/2019/03/31/zm-k44-779/8x-e21af1e554caa65b6395fbc7e13d6024eae21940-im-66,57,43-FF,FF,FF.gif) Wiersz był dowolny, czyli każda z tych liczb (np.
Wiersz był dowolny, czyli każda z tych liczb (np. 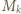 ) jest obecna we wszystkich wierszach - występuje wobec tego
) jest obecna we wszystkich wierszach - występuje wobec tego 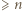 razy. To uzasadnia odpowiedź.
razy. To uzasadnia odpowiedź.