Zadanie ZM-1414
o zadaniu...
- Publikacja w Delcie: grudzień 2016
- Publikacja elektroniczna: 30 listopada 2016
Każda z liczb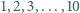 
została wpisana na dziesięciu polach szachownicy 
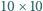w taki sposób, że na każdym polu jest dokładnie jedna liczba. Wykazać, że istnieje wiersz lub kolumna tej szachownicy, w której występują co najmniej 
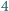różne liczby.
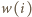oraz 
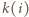oznaczają odpowiednio liczbę wierszy i kolumn, zawierających liczbę 
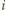dla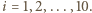 
Ponieważ każda z dziesięciu liczb 
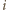umieszczonych w tablicy leży na skrzyżowaniu jednego z 
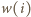wierszy z jedną z 
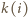kolumn, to dla każdego 
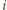spełniona jest nierówność 
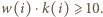W takim razie również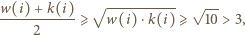
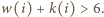
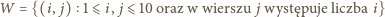
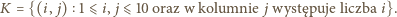
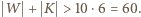Bez straty ogólności przyjmijmy, że 
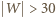(przypadek 
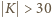rozważa się analogicznie). Z zasady szufladkowej Dirichleta wiemy, że w takim razie dla pewnego 
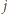zbiór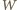 
zawiera co najmniej 
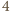pary postaci 
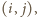a to daje tezę.