Aby udowodnić równoważność, wykażemy osobno dwie implikacje.
Ponumerujmy osoby obecne na przyjęciu liczbami od 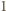 do
do  oraz oznaczmy liczbę wszystkich powitań przez
oraz oznaczmy liczbę wszystkich powitań przez 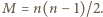 Niech
Niech 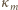 będzie permutacją zbioru
będzie permutacją zbioru 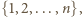 która liczbie
która liczbie 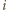 przyporządkowuje numer osoby, mającej na głowie kapelusz
przyporządkowuje numer osoby, mającej na głowie kapelusz 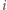 -tej osoby po
-tej osoby po  -tym powitaniu. Mamy więc
-tym powitaniu. Mamy więc 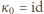 oraz
oraz 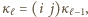 gdzie
gdzie 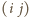 jest transpozycją, a
jest transpozycją, a 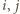 to numery osób uczestniczących w
to numery osób uczestniczących w 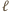 -tym powitaniu.
-tym powitaniu.
Wobec tego 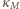 jest iloczynem
jest iloczynem 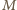 transpozycji (wszystkich możliwych par elementów zbioru
transpozycji (wszystkich możliwych par elementów zbioru 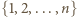 ). Z drugiej strony, w myśl warunków zadania,
). Z drugiej strony, w myśl warunków zadania, 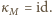 Ponieważ identyczność jest permutacją parzystą, więc wynika z tego, że
Ponieważ identyczność jest permutacją parzystą, więc wynika z tego, że 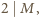 skąd uzyskujemy
skąd uzyskujemy 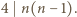 To oznacza, że jeżeli opisana sytuacja jest możliwa, to
To oznacza, że jeżeli opisana sytuacja jest możliwa, to 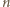 daje resztę 0 lub 1 przy dzieleniu przez 4.
daje resztę 0 lub 1 przy dzieleniu przez 4.
Aby uzasadnić, że dla każdego 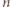 dającego resztę 0 lub 1 przy dzieleniu przez 4 istnieje kolejność powitań prowadząca do opisanej w treści zadania sytuacji, przeprowadzimy dowód indukcyjny.
dającego resztę 0 lub 1 przy dzieleniu przez 4 istnieje kolejność powitań prowadząca do opisanej w treści zadania sytuacji, przeprowadzimy dowód indukcyjny.
Jeżeli 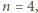 to bezpośrednio sprawdzamy, że
to bezpośrednio sprawdzamy, że
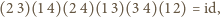
więc wystarczy, że najpierw przywitają się osoby 1 i 2, potem 3 i 4 itd.
Przypuśćmy, że dla pewnego 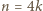 mamy odpowiednią kolejność powitań, czyli odpowiedni iloczyn transpozycji. Aby uzyskać odpowiednią kolejność dla
mamy odpowiednią kolejność powitań, czyli odpowiedni iloczyn transpozycji. Aby uzyskać odpowiednią kolejność dla 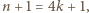 dokonajmy następujących zmian w tym iloczynie:
dokonajmy następujących zmian w tym iloczynie:
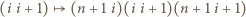
dla 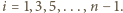 W ten sposób uzupełniliśmy iloczyn o
W ten sposób uzupełniliśmy iloczyn o 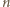 transpozycji (odpowiadających powitaniom z "nową" osobą numer
transpozycji (odpowiadających powitaniom z "nową" osobą numer 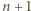 ) i łatwo sprawdzić, że warunki zadania dla nowej kolejności są spełnione.
) i łatwo sprawdzić, że warunki zadania dla nowej kolejności są spełnione.
Z kolei aby uzyskać odpowiednią kolejność dla 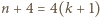 osób, dokonujemy podobnych zmian:
osób, dokonujemy podobnych zmian:
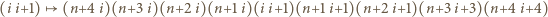
dla 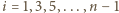 oraz dołączamy (w dowolnym miejscu) zestaw sześciu kolejno po sobie następujących powitań czterech nowych osób:
oraz dołączamy (w dowolnym miejscu) zestaw sześciu kolejno po sobie następujących powitań czterech nowych osób:
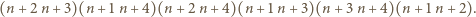
W ten sposób rozszerzyliśmy kolejność powitań w taki sposób, że znów po nastąpieniu wszystkich każdy ma znów swój kapelusz przy 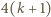 osobach. To kończy dowód indukcyjny.
osobach. To kończy dowód indukcyjny.
 osób w kapeluszach
osób w kapeluszach 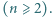 Następnie każde dwie osoby przywitały się dokładnie raz, przy czym każde powitanie polegało na zamianie kapeluszami, które w danej chwili witające się osoby miały na głowach. Okazało się, że po nastąpieniu wszystkich powitań każdy miał z powrotem swój kapelusz. Udowodnić, że taka sytuacja jest możliwa wtedy i tylko wtedy, gdy
Następnie każde dwie osoby przywitały się dokładnie raz, przy czym każde powitanie polegało na zamianie kapeluszami, które w danej chwili witające się osoby miały na głowach. Okazało się, że po nastąpieniu wszystkich powitań każdy miał z powrotem swój kapelusz. Udowodnić, że taka sytuacja jest możliwa wtedy i tylko wtedy, gdy 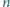 daje resztę 0 lub 1 przy dzieleniu przez 4.
daje resztę 0 lub 1 przy dzieleniu przez 4.
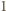 do
do  oraz oznaczmy liczbę wszystkich powitań przez
oraz oznaczmy liczbę wszystkich powitań przez 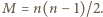 Niech
Niech 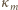 będzie permutacją zbioru
będzie permutacją zbioru 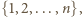 która liczbie
która liczbie 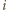 przyporządkowuje numer osoby, mającej na głowie kapelusz
przyporządkowuje numer osoby, mającej na głowie kapelusz 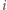 -tej osoby po
-tej osoby po  -tym powitaniu. Mamy więc
-tym powitaniu. Mamy więc 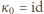 oraz
oraz 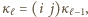 gdzie
gdzie 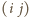 jest transpozycją, a
jest transpozycją, a 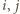 to numery osób uczestniczących w
to numery osób uczestniczących w 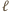 -tym powitaniu.
-tym powitaniu.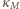 jest iloczynem
jest iloczynem 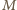 transpozycji (wszystkich możliwych par elementów zbioru
transpozycji (wszystkich możliwych par elementów zbioru 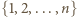 ). Z drugiej strony, w myśl warunków zadania,
). Z drugiej strony, w myśl warunków zadania, 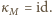 Ponieważ identyczność jest permutacją parzystą, więc wynika z tego, że
Ponieważ identyczność jest permutacją parzystą, więc wynika z tego, że 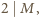 skąd uzyskujemy
skąd uzyskujemy 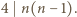 To oznacza, że jeżeli opisana sytuacja jest możliwa, to
To oznacza, że jeżeli opisana sytuacja jest możliwa, to 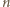 daje resztę 0 lub 1 przy dzieleniu przez 4.
daje resztę 0 lub 1 przy dzieleniu przez 4.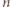 dającego resztę 0 lub 1 przy dzieleniu przez 4 istnieje kolejność powitań prowadząca do opisanej w treści zadania sytuacji, przeprowadzimy dowód indukcyjny.
dającego resztę 0 lub 1 przy dzieleniu przez 4 istnieje kolejność powitań prowadząca do opisanej w treści zadania sytuacji, przeprowadzimy dowód indukcyjny.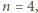 to bezpośrednio sprawdzamy, że
to bezpośrednio sprawdzamy, że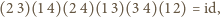
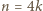 mamy odpowiednią kolejność powitań, czyli odpowiedni iloczyn transpozycji. Aby uzyskać odpowiednią kolejność dla
mamy odpowiednią kolejność powitań, czyli odpowiedni iloczyn transpozycji. Aby uzyskać odpowiednią kolejność dla 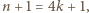 dokonajmy następujących zmian w tym iloczynie:
dokonajmy następujących zmian w tym iloczynie: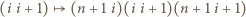
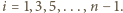 W ten sposób uzupełniliśmy iloczyn o
W ten sposób uzupełniliśmy iloczyn o 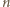 transpozycji (odpowiadających powitaniom z "nową" osobą numer
transpozycji (odpowiadających powitaniom z "nową" osobą numer 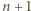 ) i łatwo sprawdzić, że warunki zadania dla nowej kolejności są spełnione.
) i łatwo sprawdzić, że warunki zadania dla nowej kolejności są spełnione.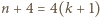 osób, dokonujemy podobnych zmian:
osób, dokonujemy podobnych zmian: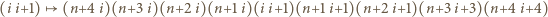
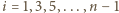 oraz dołączamy (w dowolnym miejscu) zestaw sześciu kolejno po sobie następujących powitań czterech nowych osób:
oraz dołączamy (w dowolnym miejscu) zestaw sześciu kolejno po sobie następujących powitań czterech nowych osób: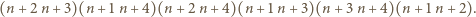
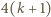 osobach. To kończy dowód indukcyjny.
osobach. To kończy dowód indukcyjny.