Zadanie ZM-1566
o zadaniu...
- Publikacja w Delcie: maj 2018
- Publikacja elektroniczna: 30 kwietnia 2018
W turnieju szachowym wzięło udział  zawodników
zawodników 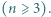 Każdy zawodnik rozegrał z każdym innym zawodnikiem dokładnie jedną partię, przy czym żadna partia nie zakończyła się remisem. Po turnieju wszyscy zawodnicy usiedli przy okrągłym stole w taki sposób, że każdy zawodnik wygrał z osobą siedzącą obok niego z jego lewej strony. Wyznaczyć, w zależności od
Każdy zawodnik rozegrał z każdym innym zawodnikiem dokładnie jedną partię, przy czym żadna partia nie zakończyła się remisem. Po turnieju wszyscy zawodnicy usiedli przy okrągłym stole w taki sposób, że każdy zawodnik wygrał z osobą siedzącą obok niego z jego lewej strony. Wyznaczyć, w zależności od 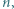 największą liczbę
największą liczbę 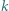 o następującej własności: istnieje (niezależnie od przebiegu turnieju) co najmniej
o następującej własności: istnieje (niezależnie od przebiegu turnieju) co najmniej 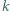 różnych takich trójek zawodników
różnych takich trójek zawodników 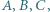 że
że 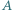 wygrał z
wygrał z 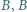 wygrał z
wygrał z 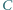 oraz
oraz 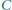 wygrał z
wygrał z 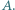


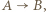 jeżeli zawodnik
jeżeli zawodnik 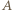 wygrał z zawodnikiem
wygrał z zawodnikiem 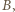 a trójkę zawodników
a trójkę zawodników 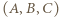 o tej własności, że
o tej własności, że 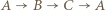 nazwijmy remisową (trójki
nazwijmy remisową (trójki 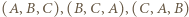 utożsamiamy).
utożsamiamy).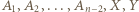 o następujących wynikach:
o następujących wynikach: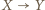 ;
;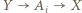 dla
dla 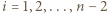 ;
;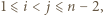 to
to 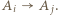
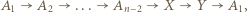
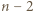 trójki remisowe, mianowicie
trójki remisowe, mianowicie 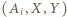 dla
dla 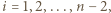 co oznacza, że
co oznacza, że 
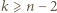 przeprowadzimy indukcyjnie. Dla
przeprowadzimy indukcyjnie. Dla 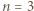 jest dokładnie jedna trójka remisowa. Przypuśćmy, że liczba trójek remisowych w turnieju z
jest dokładnie jedna trójka remisowa. Przypuśćmy, że liczba trójek remisowych w turnieju z  zawodnikami (których można odpowiednio usadzić przy okrągłym stole) jest nie mniejsza od
zawodnikami (których można odpowiednio usadzić przy okrągłym stole) jest nie mniejsza od 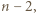 przy czym
przy czym 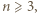 i rozważmy dowolny turniej z
i rozważmy dowolny turniej z 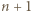 zawodnikami
zawodnikami 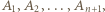 w którym
w którym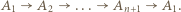
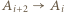 dla każdego
dla każdego 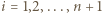 (gdzie
(gdzie 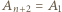 oraz
oraz 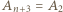 ), to każda z trójek
), to każda z trójek 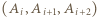 jest remisowa, więc jest ich co najmniej
jest remisowa, więc jest ich co najmniej 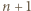 (w szczególności więcej niż
(w szczególności więcej niż 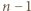 ).
).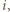 że
że 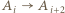 ; bez straty ogólności (ewentualnie cyklicznie przenumerowując zawodników) przypuśćmy, że
; bez straty ogólności (ewentualnie cyklicznie przenumerowując zawodników) przypuśćmy, że 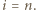 Wówczas z założenia indukcyjnego wynika, że
Wówczas z założenia indukcyjnego wynika, że 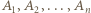 tworzą co najmniej
tworzą co najmniej 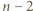 różne trójki remisowe. Wystarczy więc wykazać, że istnieje trójka remisowa, do której należy zawodnik
różne trójki remisowe. Wystarczy więc wykazać, że istnieje trójka remisowa, do której należy zawodnik 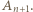 Istotnie, skoro
Istotnie, skoro 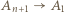 oraz
oraz 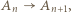 to istnieje takie
to istnieje takie 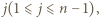 że
że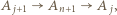
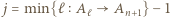 i trójka
i trójka 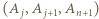 jest wówczas remisowa. To kończy dowód indukcyjny i rozwiązanie zadania.
jest wówczas remisowa. To kończy dowód indukcyjny i rozwiązanie zadania.