Zadania z matematyki - XII 2020»Zadanie 1659
o zadaniu...
- Zadanie pochodzi z artykułu Zadania z matematyki - XII 2020
- Publikacja w Delcie: grudzień 2020
- Publikacja elektroniczna: 1 grudnia 2020
Dany jest basen w kształcie pierścienia kołowego, podzielony na 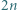 małych zbiorników poprzedzielanych zawieszonymi nad wodą obręczami
małych zbiorników poprzedzielanych zawieszonymi nad wodą obręczami  . W każdym małym zbiorniku (znajdującym się pomiędzy dwiema obręczami) pływa jeden delfin. Co jakiś czas dwa delfiny z sąsiednich zbiorników wykonują akrobację polegającą na jednoczesnym skoku przez obręcz (znajdującą się między zbiornikami) i w rezultacie - zamianie miejscami. Przypuśćmy, że po pewnym czasie każde dwa delfiny zamieniły się miejscami dokładnie raz. Wykazać, że pewna obręcz nie została użyta do wykonania żadnej akrobacji.
. W każdym małym zbiorniku (znajdującym się pomiędzy dwiema obręczami) pływa jeden delfin. Co jakiś czas dwa delfiny z sąsiednich zbiorników wykonują akrobację polegającą na jednoczesnym skoku przez obręcz (znajdującą się między zbiornikami) i w rezultacie - zamianie miejscami. Przypuśćmy, że po pewnym czasie każde dwa delfiny zamieniły się miejscami dokładnie raz. Wykazać, że pewna obręcz nie została użyta do wykonania żadnej akrobacji.
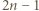

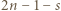
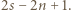



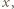


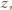

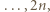
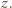

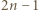

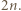
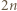
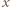
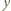


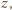
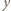 - jeszcze nie. Jednak po skoku przez obręcz między zbiornikami 1 i
- jeszcze nie. Jednak po skoku przez obręcz między zbiornikami 1 i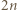
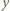


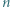
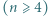 . Każda para osób rozegrała dokładnie jeden mecz, który zakończył się zwycięstwem jednej z
. Każda para osób rozegrała dokładnie jeden mecz, który zakończył się zwycięstwem jednej z
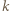
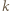 (krótko:
(krótko: 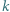 -cyklu).
-cyklu).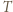

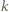 -cykl, to istnieje też
-cykl, to istnieje też 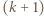 -cykl, dla
-cykl, dla 
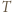
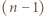 -cykl, czyli teza zadania.
-cykl, czyli teza zadania.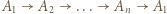
 -cyklem oraz niech
-cyklem oraz niech 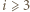
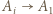 (zbiór takich indeksów jest niepusty, gdyż należy do niego
(zbiór takich indeksów jest niepusty, gdyż należy do niego  ). Wówczas
). Wówczas 
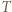
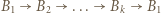
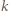 -cyklem, gdzie
-cyklem, gdzie 
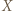

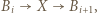
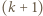 -cykl poprzez wstawienie
-cykl poprzez wstawienie 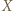
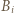
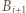 (przyjmujemy
(przyjmujemy 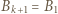 ). W
). W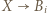
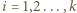

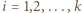 ; niech
; niech 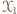
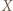
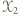 - zbiorem wierzchołków
- zbiorem wierzchołków 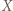
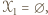
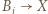
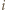
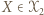 - nie mógłby wtedy jednak istnieć
- nie mógłby wtedy jednak istnieć 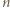 -cykl w
-cykl w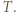
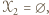
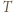
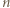 -cykl. Również gdyby
-cykl. Również gdyby 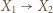
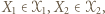
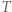
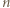 -cykl. Stąd wniosek, że istnieją wierzchołki
-cykl. Stąd wniosek, że istnieją wierzchołki 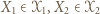
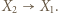
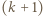 -cykl
-cykl
 -osobowych stołach usiadło
-osobowych stołach usiadło 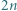
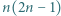

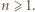
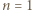


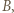
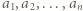

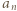
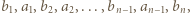
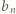
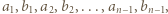
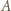
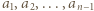
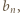
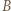
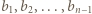
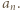
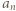

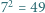
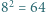
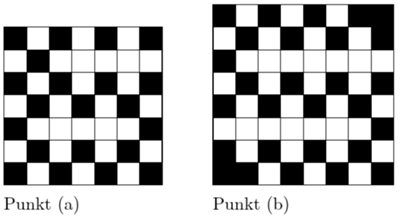
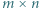 wpisano pewną liczbę rzeczywistą. W danej chwili możemy wybrać jedną kolumnę lub wiersz tej tabeli i zmienić znaki występujących w nim liczb na przeciwne. Wykazać, że stosując takie operacje, można doprowadzić do tego, by suma liczb w każdym wierszu i w każdej kolumnie była nieujemna.
wpisano pewną liczbę rzeczywistą. W danej chwili możemy wybrać jedną kolumnę lub wiersz tej tabeli i zmienić znaki występujących w nim liczb na przeciwne. Wykazać, że stosując takie operacje, można doprowadzić do tego, by suma liczb w każdym wierszu i w każdej kolumnie była nieujemna.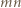 liczb, a ta może przyjąć jedynie skończenie wiele wartości.
liczb, a ta może przyjąć jedynie skończenie wiele wartości. żołnierzy. Na komendę Na lewo patrz! część z nich odwraca się w lewo, a część w prawo. Następnie co sekundę wszyscy żołnierze, którzy stoją obok siebie i są zwróceni do siebie twarzami, obracają się o
żołnierzy. Na komendę Na lewo patrz! część z nich odwraca się w lewo, a część w prawo. Następnie co sekundę wszyscy żołnierze, którzy stoją obok siebie i są zwróceni do siebie twarzami, obracają się o  Wykazać, że po pewnym czasie żołnierze przestaną się obracać.
Wykazać, że po pewnym czasie żołnierze przestaną się obracać.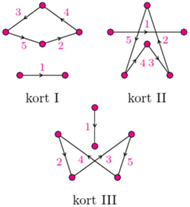
 który dotąd grał tylko na pierwszym korcie, i zawodnik
który dotąd grał tylko na pierwszym korcie, i zawodnik  który dotąd grał tylko na drugim korcie. Ci zawodnicy nie grali jeszcze ze sobą, więc powinni zagrać w trzeciej rundzie - ale nie mają gdzie (gdyby zagrali na pierwszym korcie,
który dotąd grał tylko na drugim korcie. Ci zawodnicy nie grali jeszcze ze sobą, więc powinni zagrać w trzeciej rundzie - ale nie mają gdzie (gdyby zagrali na pierwszym korcie,  powtórzyłby połówkę, a gdyby na drugim -
powtórzyłby połówkę, a gdyby na drugim - 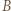 powtórzyłby połówkę). Uzyskana sprzeczność oznacza, że nie jest możliwy taki układ rozgrywek.
powtórzyłby połówkę). Uzyskana sprzeczność oznacza, że nie jest możliwy taki układ rozgrywek.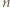 będzie liczbą uczestników pewnego kółka, spełniającego opisane w zadaniu warunki. Udowodnimy, że
będzie liczbą uczestników pewnego kółka, spełniającego opisane w zadaniu warunki. Udowodnimy, że 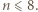 Przydatny okaże się następujący lemat, którego dowód można znaleźć na przykład w Wikipedii pod hasłem twierdzenie Ramseya:
Przydatny okaże się następujący lemat, którego dowód można znaleźć na przykład w Wikipedii pod hasłem twierdzenie Ramseya: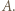 Przypuśćmy, że lubi on pewnych 6 uczestników. Zgodnie z założeniem zadania oraz powyższym lematem wśród nich znajduje się 3, którzy wzajemnie się lubią, i razem z
Przypuśćmy, że lubi on pewnych 6 uczestników. Zgodnie z założeniem zadania oraz powyższym lematem wśród nich znajduje się 3, którzy wzajemnie się lubią, i razem z 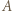 tworzą oni czwórkę, która przeczy założeniom zadania. Przypuśćmy teraz, że
tworzą oni czwórkę, która przeczy założeniom zadania. Przypuśćmy teraz, że 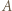 nie lubi pewnych 4 uczestników. Wśród nich znajduje się dwóch, którzy się nie lubią, i razem z
nie lubi pewnych 4 uczestników. Wśród nich znajduje się dwóch, którzy się nie lubią, i razem z 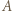 tworzą oni trójkę sprzeczną z założeniami. Wynika stąd, że
tworzą oni trójkę sprzeczną z założeniami. Wynika stąd, że 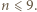 Gdyby jednak
Gdyby jednak 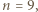 to każdy uczestnik musiałby lubić dokładnie 5 uczestników. Jest to sprzeczność, gdyż suma liczb sympatii poszczególnych uczestników wyniosłaby 45, a musi to być liczba parzysta ze względu na wzajemność uczuć. W tej sytuacji
to każdy uczestnik musiałby lubić dokładnie 5 uczestników. Jest to sprzeczność, gdyż suma liczb sympatii poszczególnych uczestników wyniosłaby 45, a musi to być liczba parzysta ze względu na wzajemność uczuć. W tej sytuacji 
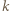 i
i 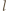 lubią się tylko wtedy, gdy
lubią się tylko wtedy, gdy 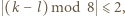 to ta grupka będzie spełniać warunki zadania, co kończy rozwiązanie.
to ta grupka będzie spełniać warunki zadania, co kończy rozwiązanie.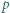
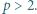


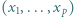
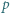 ), że
), że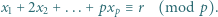
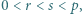
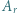
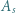
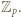
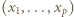



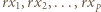
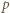
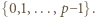
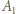 - czyli spełniała zależność
- czyli spełniała zależność 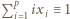 (mod
(mod  ) - to po pomnożeniu wszystkich jej wyrazów przez
) - to po pomnożeniu wszystkich jej wyrazów przez 
 - czyli permutację należącą do zbioru
- czyli permutację należącą do zbioru 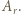
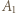
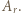
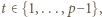
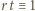 (mod
(mod  ) (taki element
) (taki element 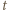
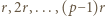
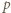
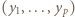

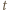
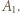
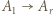 (mnożenie przez
(mnożenie przez  ) oraz
) oraz 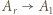 (mnożenie przez
(mnożenie przez 
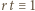 ) są wzajemnie odwrotne. To dowodzi, że zbiór
) są wzajemnie odwrotne. To dowodzi, że zbiór 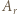
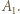
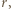
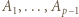
 i
i 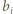 będą odpowiednio liczbami dziewczynek i chłopców startujących z
będą odpowiednio liczbami dziewczynek i chłopców startujących z  -tej szkoły. Niech ponadto
-tej szkoły. Niech ponadto  będzie liczbą singli, a
będzie liczbą singli, a 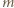 liczbą miksów. Wówczas
liczbą miksów. Wówczas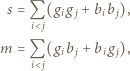
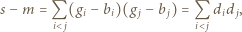
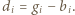 Z założeń zadania
Z założeń zadania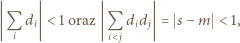
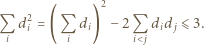
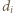 są różne od 0, co kończy rozwiązanie.
są różne od 0, co kończy rozwiązanie.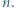 Każdy element zbioru
Każdy element zbioru 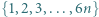 pomalowano na biało albo na czarno, przy czym dokładnie
pomalowano na biało albo na czarno, przy czym dokładnie  elementów jest białych. Wykazać, że w tym zbiorze istnieje
elementów jest białych. Wykazać, że w tym zbiorze istnieje 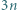 kolejnych liczb całkowitych, wśród których dokładnie
kolejnych liczb całkowitych, wśród których dokładnie  liczb jest białych.
liczb jest białych.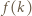 dla
dla 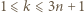 będzie liczbą elementów zbioru
będzie liczbą elementów zbioru 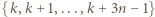 pomalowanych na biało. Zauważmy, że
pomalowanych na biało. Zauważmy, że 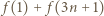 jest liczbą elementów zbioru
jest liczbą elementów zbioru 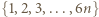 pomalowanych na biało, czyli
pomalowanych na biało, czyli  Jeśli
Jeśli 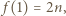 to teza zadania zachodzi. W przeciwnym razie
to teza zadania zachodzi. W przeciwnym razie 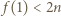 albo
albo 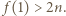 Przyjmijmy bez straty ogólności, że spełniony jest pierwszy przypadek (drugi jest analogiczny). Wtedy
Przyjmijmy bez straty ogólności, że spełniony jest pierwszy przypadek (drugi jest analogiczny). Wtedy 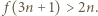 Jest jasne, że
Jest jasne, że 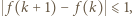 zatem istnieje taka liczba
zatem istnieje taka liczba 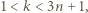 dla której mamy
dla której mamy 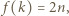 co jest równoważne z tezą zadania.
co jest równoważne z tezą zadania.
 . Wiersze są numerowane od zera; zatem w
. Wiersze są numerowane od zera; zatem w  -tym wierszu jest
-tym wierszu jest 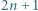 liczb dodatnich.
liczb dodatnich.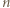 -tego wiersza jako kolejne współczynniki wielomianu stopnia
-tego wiersza jako kolejne współczynniki wielomianu stopnia 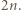 Mnożąc ów wielomian przez trójmian
Mnożąc ów wielomian przez trójmian 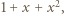 otrzymujemy wielomian stopnia
otrzymujemy wielomian stopnia 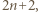 którego kolejnymi współczynnikami są wyrazy następnego wiersza tabeli - bo taka jest zasada generowania kolejnych wierszy. Stąd wniosek, że wyrazy
którego kolejnymi współczynnikami są wyrazy następnego wiersza tabeli - bo taka jest zasada generowania kolejnych wierszy. Stąd wniosek, że wyrazy  -tego wiersza to kolejne współczynniki wielomianu
-tego wiersza to kolejne współczynniki wielomianu 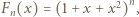 zapisanego w postaci rozwiniętej.
zapisanego w postaci rozwiniętej.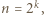 to wyrazy
to wyrazy 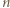 -tego wiersza, poza wspomnianymi trzema, są liczbami parzystymi. Uzasadnienie indukcyjne: tak jest dla
-tego wiersza, poza wspomnianymi trzema, są liczbami parzystymi. Uzasadnienie indukcyjne: tak jest dla  ; i jeśli tak jest dla
; i jeśli tak jest dla 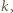 to podnosząc wielomian
to podnosząc wielomian 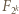 do kwadratu dostajemy wielomian
do kwadratu dostajemy wielomian  utworzony przez kwadraty składników wielomianu
utworzony przez kwadraty składników wielomianu 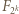 (ich współczynniki nie zmieniają parzystości) plus liczne podwojone iloczyny, dające współczynniki parzyste.
(ich współczynniki nie zmieniają parzystości) plus liczne podwojone iloczyny, dające współczynniki parzyste. oraz
oraz 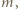 przy czym
przy czym 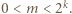 Wykażemy, że w wierszu o numerze
Wykażemy, że w wierszu o numerze 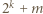 na pozycji
na pozycji  znajduje się liczba nieparzysta, zaś na pozycji
znajduje się liczba nieparzysta, zaś na pozycji 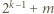 liczba parzysta.
liczba parzysta.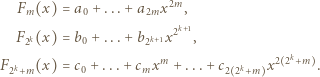
 wyraża się wzorem
wyraża się wzorem
 w nawiasie są parzyste (jako współczynniki wielomianu
w nawiasie są parzyste (jako współczynniki wielomianu  z pozycji nie skrajnych ani nie środkowej); liczba
z pozycji nie skrajnych ani nie środkowej); liczba  jest nieparzysta (środkowy wyraz
jest nieparzysta (środkowy wyraz 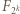 ). Zatem liczba
). Zatem liczba  jest nieparzysta.
jest nieparzysta. widzimy w wielomianie
widzimy w wielomianie  współczynnik
współczynnik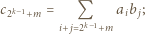
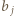 mamy tylko dla
mamy tylko dla  oraz
oraz 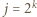 (środkowy wyraz w
(środkowy wyraz w 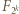 ); towarzyszą im czynniki
); towarzyszą im czynniki  oraz
oraz 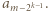 Te dwie liczby są położone w wierszu
Te dwie liczby są położone w wierszu 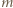 symetrycznie względem wyrazu środkowego
symetrycznie względem wyrazu środkowego 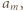 więc są równe.
więc są równe.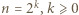 (bowiem gdy
(bowiem gdy 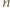 nie jest potęgą dwójki,
nie jest potęgą dwójki, 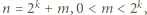 znaleziona liczba nieparzysta
znaleziona liczba nieparzysta 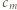 leży w wierszu
leży w wierszu  na pozycji
na pozycji  więc nie na skraju ani nie na środku).
więc nie na skraju ani nie na środku).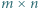 w taki sposób, aby każda wieża była atakowana przez dokładnie jedną inną wieżę.
w taki sposób, aby każda wieża była atakowana przez dokładnie jedną inną wieżę.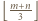 . Ponadto w każdej linii mogą pojawić się co najwyżej dwie wieże. Łącząc powyższe obserwacje, uzyskujemy, że liczba wież nie przekracza
. Ponadto w każdej linii mogą pojawić się co najwyżej dwie wieże. Łącząc powyższe obserwacje, uzyskujemy, że liczba wież nie przekracza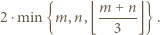
 oraz, że
oraz, że 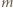 to liczba kolumn, a
to liczba kolumn, a  - liczba wierszy. Nietrudno wskazać przykład, że jeśli
- liczba wierszy. Nietrudno wskazać przykład, że jeśli 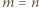 , to można osiągnąć ustawienie
, to można osiągnąć ustawienie  wież. Jeżeli
wież. Jeżeli 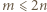 , to w
, to w  wierszach umieszczamy po dwie wieże, tym samym redukując szachownicę do kwadratu o boku
wierszach umieszczamy po dwie wieże, tym samym redukując szachownicę do kwadratu o boku 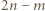 i wobec obserwacji z poprzedniego zdania, znów otrzymujemy ustawienie realizujące
i wobec obserwacji z poprzedniego zdania, znów otrzymujemy ustawienie realizujące 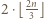 wież. Wreszcie dla
wież. Wreszcie dla  ustawiamy po dwie wieże w każdym wierszu i otrzymujemy ustawienie
ustawiamy po dwie wieże w każdym wierszu i otrzymujemy ustawienie 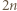 wież.
wież. w taki sposób, aby każda wieża była atakowana przez dokładnie dwie inne wieże.
w taki sposób, aby każda wieża była atakowana przez dokładnie dwie inne wieże. wież (po jednej na każdą jednostkę obwodu szachownicy). Zauważmy, że każda prawdziwa wieża jest atakowana przez dokładnie dwie wieże dodatkowe. Stąd wniosek, że liczba wież prawdziwych nie przekracza połowy liczby wież dodatkowych, czyli
wież (po jednej na każdą jednostkę obwodu szachownicy). Zauważmy, że każda prawdziwa wieża jest atakowana przez dokładnie dwie wieże dodatkowe. Stąd wniosek, że liczba wież prawdziwych nie przekracza połowy liczby wież dodatkowych, czyli 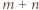 . Ustawiając wieże w czterech narożnikach szachownicy oraz wzdłuż dwóch jej prostopadłych boków, uzyskujemy przykład realizujący to szacowanie.
. Ustawiając wieże w czterech narożnikach szachownicy oraz wzdłuż dwóch jej prostopadłych boków, uzyskujemy przykład realizujący to szacowanie.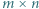 w taki sposób, aby każda wieża, która nie znajduje się w narożniku szachownicy, była atakowana przez dokładnie trzy inne wieże.
w taki sposób, aby każda wieża, która nie znajduje się w narożniku szachownicy, była atakowana przez dokładnie trzy inne wieże.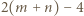 pól szachownicy przylegających do jej brzegu nazwijmy brzegowym. Zauważmy, że każda wieża, która sama nie znajduje się na polu brzegowym, atakuje dokładnie jedno puste (czyli niezajęte przez inną wieżę) pole brzegowe. Wobec tego łączna liczba wież jest nie większa od liczby pól brzegowych. Z drugiej strony, ustawiając wieże na wszystkich polach brzegowych, uzyskujemy konfigurację, która spełnia warunki zadania.
pól szachownicy przylegających do jej brzegu nazwijmy brzegowym. Zauważmy, że każda wieża, która sama nie znajduje się na polu brzegowym, atakuje dokładnie jedno puste (czyli niezajęte przez inną wieżę) pole brzegowe. Wobec tego łączna liczba wież jest nie większa od liczby pól brzegowych. Z drugiej strony, ustawiając wieże na wszystkich polach brzegowych, uzyskujemy konfigurację, która spełnia warunki zadania.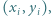
 spośród których nie można wybrać czterech wierzchołków równoległoboku.
spośród których nie można wybrać czterech wierzchołków równoległoboku.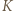 będzie zbiorem punktów o współrzędnych należących do zbioru
będzie zbiorem punktów o współrzędnych należących do zbioru 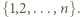 Niech
Niech  będzie zbiorem punktów należących do
będzie zbiorem punktów należących do 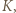 których co najmniej jedna współrzędna jest równa 1. Wówczas w
których co najmniej jedna współrzędna jest równa 1. Wówczas w 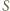 nie ma 4 punktów będących wierzchołkami równoległoboku, zatem szukana liczba nie przekracza liczności
nie ma 4 punktów będących wierzchołkami równoległoboku, zatem szukana liczba nie przekracza liczności 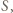 czyli
czyli 
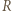 zbioru
zbioru 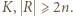 Przypuśćmy, że w
Przypuśćmy, że w 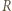 nie ma 4 wierzchołków równoległoboku. Dla
nie ma 4 wierzchołków równoległoboku. Dla  niech
niech  będzie zbiorem punktów należących do
będzie zbiorem punktów należących do 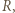 których pierwsza współrzędna wynosi
których pierwsza współrzędna wynosi 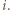 Niech
Niech 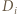 będzie zbiorem odległości "najniższego" punktu zbioru
będzie zbiorem odległości "najniższego" punktu zbioru 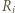 od pozostałych punktów tego zbioru. Wówczas
od pozostałych punktów tego zbioru. Wówczas 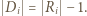 Ponadto, ze względu na przypuszczenie o braku równoległoboku, zbiory
Ponadto, ze względu na przypuszczenie o braku równoległoboku, zbiory  muszą być parami rozłączne, a zatem
muszą być parami rozłączne, a zatem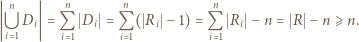
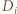 jest podzbiorem
jest podzbiorem  więc lewa strona powyższej nierówności nie może przekraczać
więc lewa strona powyższej nierówności nie może przekraczać 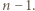 Wobec przedstawionych rozważań odpowiedzią na pytanie z zadania jest
Wobec przedstawionych rozważań odpowiedzią na pytanie z zadania jest 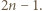
 o następującej własności: Liczby całkowite od
o następującej własności: Liczby całkowite od 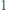 do
do  można tak wpisać w pola tablicy
można tak wpisać w pola tablicy 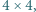 aby sumy liczb w wierszach i kolumnach były ośmioma parami różnymi liczbami całkowitymi, z których każda jest podzielna przez
aby sumy liczb w wierszach i kolumnach były ośmioma parami różnymi liczbami całkowitymi, z których każda jest podzielna przez 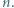
 oraz
oraz 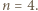
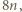 a z drugiej - nie większa od
a z drugiej - nie większa od 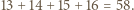 Stąd wniosek, że
Stąd wniosek, że 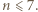 Ponadto suma ośmiu rozważanych sum jest równa dwukrotności sumy wszystkich liczb wpisanych w pola tablicy, czyli
Ponadto suma ośmiu rozważanych sum jest równa dwukrotności sumy wszystkich liczb wpisanych w pola tablicy, czyli 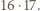 Liczba
Liczba 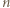 jest dzielnikiem tej sumy, wobec czego
jest dzielnikiem tej sumy, wobec czego  lub
lub 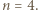 Poniższy przykład pozwala stwierdzić, że te wartości
Poniższy przykład pozwala stwierdzić, że te wartości 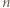 w istocie są osiągalne.
w istocie są osiągalne.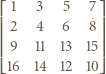
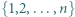 mają tę samą sumę elementów. Wykazać, że każdy z tych podzbiorów ma mniej niż
mają tę samą sumę elementów. Wykazać, że każdy z tych podzbiorów ma mniej niż 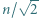 elementów.
elementów. wspólną wartość sumy elementów w obydwu podzbiorach. Wówczas
wspólną wartość sumy elementów w obydwu podzbiorach. Wówczas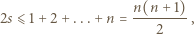
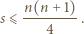
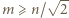 elementów, to jego suma elementów byłaby nie mniejsza od
elementów, to jego suma elementów byłaby nie mniejsza od 
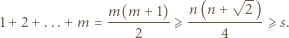
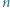 jednakowych świeczek. Pierwszego dnia zapalamy jedną świeczkę na dokładnie godzinę. Drugiego dnia wybieramy dwie świeczki i zapalamy je również na godzinę. Ogólnie
jednakowych świeczek. Pierwszego dnia zapalamy jedną świeczkę na dokładnie godzinę. Drugiego dnia wybieramy dwie świeczki i zapalamy je również na godzinę. Ogólnie  -tego dnia pewnych
-tego dnia pewnych 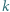 świeczek pali się przez godzinę. Przypuśćmy, że
świeczek pali się przez godzinę. Przypuśćmy, że 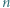 -tego dnia po upływie godziny wszystkie świeczki wypaliły się równocześnie. Wyznaczyć wszystkie wartości
-tego dnia po upływie godziny wszystkie świeczki wypaliły się równocześnie. Wyznaczyć wszystkie wartości 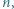 dla których taka sytuacja jest możliwa.
dla których taka sytuacja jest możliwa.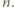
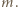 Wówczas łączny czas (w godzinach) płonięcia wszystkich świeczek to z jednej strony
Wówczas łączny czas (w godzinach) płonięcia wszystkich świeczek to z jednej strony 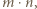 a z drugiej
a z drugiej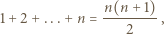
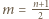 i w konsekwencji, aby opisana sytuacja mogła mieć miejsce,
i w konsekwencji, aby opisana sytuacja mogła mieć miejsce, 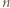 musi być liczbą nieparzystą.
musi być liczbą nieparzystą.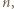 powiedzmy
powiedzmy 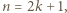 gdzie
gdzie 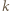 jest liczbą całkowitą nieujemną, można tak zaplanować, które świeczki będą zapalane danego dnia, aby warunki zadania zostały spełnione. Przykładowo, jeśli ponumerujemy świeczki od
jest liczbą całkowitą nieujemną, można tak zaplanować, które świeczki będą zapalane danego dnia, aby warunki zadania zostały spełnione. Przykładowo, jeśli ponumerujemy świeczki od 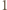 do
do  to możemy
to możemy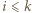 :
: 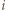 -tego dnia zapalić wszystkie świeczki o numerach od
-tego dnia zapalić wszystkie świeczki o numerach od 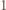 do
do 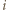 ;
;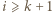 :
: 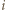 -tego dnia zapalić wszystkie świeczki o numerach od
-tego dnia zapalić wszystkie świeczki o numerach od 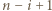 do
do 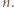
 kart oznaczonych liczbami
kart oznaczonych liczbami  ułożonych w losowej kolejności. Wielokrotnie wykonujemy następującą operację: Jeśli karta na górze stosu ma numer
ułożonych w losowej kolejności. Wielokrotnie wykonujemy następującą operację: Jeśli karta na górze stosu ma numer 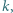 to odwracamy kolejność wierzchnich
to odwracamy kolejność wierzchnich 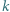 kart. Wykazać, że w końcu na górze pojawi się karta o numerze
kart. Wykazać, że w końcu na górze pojawi się karta o numerze 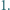
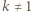 raz pojawi się na górze stosu, to aby pojawiła się tam ponownie, wcześniej musi się tam znaleźć liczba większa od
raz pojawi się na górze stosu, to aby pojawiła się tam ponownie, wcześniej musi się tam znaleźć liczba większa od 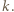 W szczególności
W szczególności 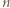 pojawi się na górze co najwyżej raz. Jeśli to nastąpi, to
pojawi się na górze co najwyżej raz. Jeśli to nastąpi, to 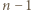 pojawi się później co najwyżej raz, jeżeli nie, to
pojawi się później co najwyżej raz, jeżeli nie, to  również pojawi się w ogóle co najwyżej raz. Po ewentualnym wystąpieniu
również pojawi się w ogóle co najwyżej raz. Po ewentualnym wystąpieniu 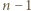 liczba
liczba 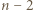 pojawi się co najwyżej raz itd. To oznacza, że w pewnym momencie na górze musi pojawić się liczba
pojawi się co najwyżej raz itd. To oznacza, że w pewnym momencie na górze musi pojawić się liczba 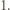
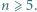 Wykazać, że elementy zbioru
Wykazać, że elementy zbioru 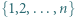 można tak pokolorować na czerwono i niebiesko, że suma czerwonych liczb jest równa iloczynowi niebieskich liczb.
można tak pokolorować na czerwono i niebiesko, że suma czerwonych liczb jest równa iloczynowi niebieskich liczb. jest liczbą nieparzystą, czyli
jest liczbą nieparzystą, czyli  dla pewnej liczby całkowitej
dla pewnej liczby całkowitej 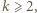 to na niebiesko malujemy liczby
to na niebiesko malujemy liczby 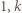 oraz
oraz  a na czerwono - wszystkie pozostałe. Wówczas suma czerwonych liczb jest równa
a na czerwono - wszystkie pozostałe. Wówczas suma czerwonych liczb jest równa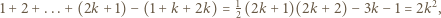
 jest liczbą parzystą, czyli
jest liczbą parzystą, czyli 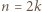 dla pewnej liczby całkowitej
dla pewnej liczby całkowitej 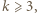 to na niebiesko malujemy liczby
to na niebiesko malujemy liczby 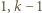 oraz
oraz 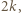 a na czerwono - wszystkie pozostałe. Wówczas suma czerwonych liczb jest równa
a na czerwono - wszystkie pozostałe. Wówczas suma czerwonych liczb jest równa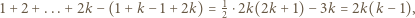
 osób, przy czym każda z nich zna dokładnie trzech innych uczestników konferencji. Czy wynika z tego, że wszystkich uczestników można zakwaterować w
osób, przy czym każda z nich zna dokładnie trzech innych uczestników konferencji. Czy wynika z tego, że wszystkich uczestników można zakwaterować w  pokojach dwuosobowych tak, aby każdy był w pokoju ze swoim znajomym?
pokojach dwuosobowych tak, aby każdy był w pokoju ze swoim znajomym?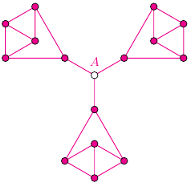
 pozostali uczestnicy dzielą się na dwie grupy
pozostali uczestnicy dzielą się na dwie grupy 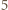 -osobowe i jedną
-osobowe i jedną 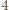 -osobową o tej własności, że każdy ma niezakwaterowanych dotąd znajomych tylko w obrębie danej grupy. Żadnej z grup
-osobową o tej własności, że każdy ma niezakwaterowanych dotąd znajomych tylko w obrębie danej grupy. Żadnej z grup 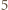 -osobowych nie da się zakwaterować w dwuosobowych pokojach.
-osobowych nie da się zakwaterować w dwuosobowych pokojach.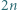 osób, przy czym każda z nich zna dokładnie trzech innych uczestników konferencji. Co więcej, wszystkich uczestników można tak posadzić przy okrągłym stole, aby każdy siedział pomiędzy dwoma spośród swoich znajomych. Wykazać, że wszystkich uczestników można na co najmniej trzy różne sposoby zakwaterować w
osób, przy czym każda z nich zna dokładnie trzech innych uczestników konferencji. Co więcej, wszystkich uczestników można tak posadzić przy okrągłym stole, aby każdy siedział pomiędzy dwoma spośród swoich znajomych. Wykazać, że wszystkich uczestników można na co najmniej trzy różne sposoby zakwaterować w  pokojach dwuosobowych tak, aby każdy był w pokoju ze swoim znajomym. Dwa sposoby zakwaterowania uznajemy za różne, jeśli co najmniej jedna osoba ma w nich innego współlokatora.
pokojach dwuosobowych tak, aby każdy był w pokoju ze swoim znajomym. Dwa sposoby zakwaterowania uznajemy za różne, jeśli co najmniej jedna osoba ma w nich innego współlokatora.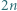 drużyn. Pierwszego dnia odbyło się
drużyn. Pierwszego dnia odbyło się 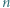 meczów, przy czym każda drużyna rozegrała dokładnie jeden mecz. Podobnie drugiego dnia każda drużyna rozegrała dokładnie jeden mecz, z inną drużyną niż pierwszego dnia. Wykazać, że po dwóch dniach rozgrywek można wskazać
meczów, przy czym każda drużyna rozegrała dokładnie jeden mecz. Podobnie drugiego dnia każda drużyna rozegrała dokładnie jeden mecz, z inną drużyną niż pierwszego dnia. Wykazać, że po dwóch dniach rozgrywek można wskazać 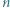 drużyn o tej własności, że żadne dwie jeszcze ze sobą nie grały.
drużyn o tej własności, że żadne dwie jeszcze ze sobą nie grały. punktów przestrzeni, z których żadne trzy nie leżą na jednej prostej. Jeśli dwie drużyny rozegrały ze sobą mecz pierwszego dnia, połączmy odpowiadające im punkty odcinkiem niebieskim, a jeśli drugiego dnia - odcinkiem czerwonym.
punktów przestrzeni, z których żadne trzy nie leżą na jednej prostej. Jeśli dwie drużyny rozegrały ze sobą mecz pierwszego dnia, połączmy odpowiadające im punkty odcinkiem niebieskim, a jeśli drugiego dnia - odcinkiem czerwonym. punktów, z których żadne dwa nie są połączone odcinkiem. Drużyny odpowiadające tym punktom mają więc żądaną własność.
punktów, z których żadne dwa nie są połączone odcinkiem. Drużyny odpowiadające tym punktom mają więc żądaną własność.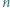 wyznaczyć największą liczbę
wyznaczyć największą liczbę 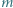 taką, że przy każdym wypełnieniu planszy
taką, że przy każdym wypełnieniu planszy 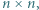 zgodnym z podanym warunkiem, pewna liczba pojawia się na co najmniej
zgodnym z podanym warunkiem, pewna liczba pojawia się na co najmniej 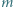 polach planszy.
polach planszy.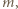 o jakiej mowa, to
o jakiej mowa, to 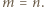 Macierz
Macierz ![|[ai j]](/math/temat/matematyka/kombinatoryka/zadania/2019/03/31/zm-k44-779/3x-0ea823dd3c43a983e9f06ad8aefabe5d4b92bbfe-im-66,57,43-FF,FF,FF.gif) o wyrazach
o wyrazach 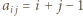
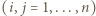 daje przykład wypełnienia planszy, przy którym liczba
daje przykład wypełnienia planszy, przy którym liczba 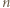 pojawia się
pojawia się  razy (cała jedna przekątna), a żadna liczba nie występuje więcej niż
razy (cała jedna przekątna), a żadna liczba nie występuje więcej niż 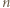 razy. Pozostaje wykazać, że przy każdym wypełnieniu planszy, zgodnym z podanym warunkiem, pewna liczba wystąpi
razy. Pozostaje wykazać, że przy każdym wypełnieniu planszy, zgodnym z podanym warunkiem, pewna liczba wystąpi 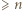 razy.
razy.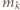 oraz
oraz 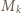 oznaczają najmniejszą oraz największą liczbę w kolumnie
oznaczają najmniejszą oraz największą liczbę w kolumnie  Liczby w sąsiednich polach różnią się co najwyżej o 1, więc w
Liczby w sąsiednich polach różnią się co najwyżej o 1, więc w 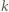 -tej kolumnie są wszystkie liczby całkowite z przedziału
-tej kolumnie są wszystkie liczby całkowite z przedziału ![k]. [mk,](/math/temat/matematyka/kombinatoryka/zadania/2019/03/31/zm-k44-779/5x-3851dd7da0ebfd80395100c363b83f096c5c4a58-im-66,57,43-FF,FF,FF.gif)
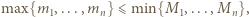 wówczas pewna liczba całkowita należy do wszystkich przedziałów
wówczas pewna liczba całkowita należy do wszystkich przedziałów ![1],...,[mn,Mn]. [m1,](/math/temat/matematyka/kombinatoryka/zadania/2019/03/31/zm-k44-779/2x-a07165ea6eadac3996e30bccf992e2921733620d-im-66,57,43-FF,FF,FF.gif) Jest ona obecna we wszystkich kolumnach, więc występuje
Jest ona obecna we wszystkich kolumnach, więc występuje 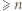 -krotnie na planszy.
-krotnie na planszy. znaczy to, że dla pewnych numerów kolumn
znaczy to, że dla pewnych numerów kolumn 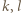 zachodzi nierówność
zachodzi nierówność 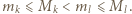 Weźmy dowolny wiersz. Na przecięciu z kolumnami
Weźmy dowolny wiersz. Na przecięciu z kolumnami  i
i 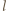 są w tym wierszu: pewna liczba
są w tym wierszu: pewna liczba 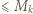 oraz pewna liczba
oraz pewna liczba 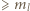 ; zatem są w tym wierszu wszystkie liczby całkowite z przedziału
; zatem są w tym wierszu wszystkie liczby całkowite z przedziału ![,m]. [M kl](/math/temat/matematyka/kombinatoryka/zadania/2019/03/31/zm-k44-779/8x-e21af1e554caa65b6395fbc7e13d6024eae21940-im-66,57,43-FF,FF,FF.gif) Wiersz był dowolny, czyli każda z tych liczb (np.
Wiersz był dowolny, czyli każda z tych liczb (np. 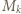 ) jest obecna we wszystkich wierszach - występuje wobec tego
) jest obecna we wszystkich wierszach - występuje wobec tego 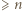 razy. To uzasadnia odpowiedź.
razy. To uzasadnia odpowiedź. punktów niebieskich leży na wspólnym okręgu. Których wielokątów jest więcej: posiadających wyłącznie niebieskie wierzchołki, czy tych, które posiadają jeden czerwony wierzchołek, a pozostałe niebieskie?
punktów niebieskich leży na wspólnym okręgu. Których wielokątów jest więcej: posiadających wyłącznie niebieskie wierzchołki, czy tych, które posiadają jeden czerwony wierzchołek, a pozostałe niebieskie? każdy
każdy  -kąt o niebieskich wierzchołkach parujemy z
-kąt o niebieskich wierzchołkach parujemy z 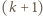 -kątem o jednym wierzchołkiem czerwonym, powstającym przez dołączenie tego wierzchołka. Bez pary pozostaną jedynie trójkąty z czerwonym wierzchołkiem, zatem wielokątów z czerwonym wierzchołkiem jest więcej.
-kątem o jednym wierzchołkiem czerwonym, powstającym przez dołączenie tego wierzchołka. Bez pary pozostaną jedynie trójkąty z czerwonym wierzchołkiem, zatem wielokątów z czerwonym wierzchołkiem jest więcej.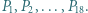 Udowodnić, że można wskazać takie
Udowodnić, że można wskazać takie 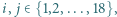 że
że 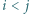 oraz żaden z pasażerów nie jechał z przystanku
oraz żaden z pasażerów nie jechał z przystanku 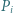 do
do 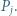
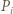 do
do  dla
dla 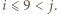 Każdy z nich siedział w tramwaju pomiędzy przystankiem
Każdy z nich siedział w tramwaju pomiędzy przystankiem 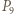 a
a 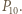
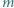 i
i 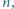 znajduje się pchła. Każdy skok pchły ma długość 1 i jest równoległy do jednego z boków. Na ile sposobów pchła może się dostać do przeciwległego wierzchołka najkrótszą drogą?
znajduje się pchła. Każdy skok pchły ma długość 1 i jest równoległy do jednego z boków. Na ile sposobów pchła może się dostać do przeciwległego wierzchołka najkrótszą drogą?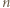 razy) i w górę (
razy) i w górę (  razy), w pewnej kolejności. Ciąg skoków pchły jest zatem ciągiem binarnym, w którym
razy), w pewnej kolejności. Ciąg skoków pchły jest zatem ciągiem binarnym, w którym  razy występuje "prawo" i
razy występuje "prawo" i 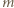 razy "góra".
razy "góra".