Zauważmy, że każdej parze atakujących się wież odpowiadają dokładnie trzy linie, w których nie znajdują się żadne inne wieże - mianowicie te linie, w których te dwie wieże się znajdują. Wobec tego liczba par wież nie przekracza 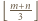 . Ponadto w każdej linii mogą pojawić się co najwyżej dwie wieże. Łącząc powyższe obserwacje, uzyskujemy, że liczba wież nie przekracza
. Ponadto w każdej linii mogą pojawić się co najwyżej dwie wieże. Łącząc powyższe obserwacje, uzyskujemy, że liczba wież nie przekracza
Udowodnimy, że powyższe wyrażenie w istocie zadaje największą możliwą liczbę wież. Przypuśćmy, bez straty ogólności, że 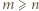 oraz, że
oraz, że 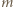 to liczba kolumn, a
to liczba kolumn, a  - liczba wierszy. Nietrudno wskazać przykład, że jeśli
- liczba wierszy. Nietrudno wskazać przykład, że jeśli 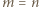 , to można osiągnąć ustawienie
, to można osiągnąć ustawienie 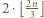 wież. Jeżeli
wież. Jeżeli 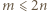 , to w
, to w 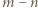 wierszach umieszczamy po dwie wieże, tym samym redukując szachownicę do kwadratu o boku
wierszach umieszczamy po dwie wieże, tym samym redukując szachownicę do kwadratu o boku 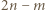 i wobec obserwacji z poprzedniego zdania, znów otrzymujemy ustawienie realizujące
i wobec obserwacji z poprzedniego zdania, znów otrzymujemy ustawienie realizujące 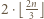 wież. Wreszcie dla
wież. Wreszcie dla 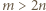 ustawiamy po dwie wieże w każdym wierszu i otrzymujemy ustawienie
ustawiamy po dwie wieże w każdym wierszu i otrzymujemy ustawienie 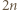 wież.
wież.
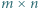 w taki sposób, aby każda wieża była atakowana przez dokładnie jedną inną wieżę.
w taki sposób, aby każda wieża była atakowana przez dokładnie jedną inną wieżę.
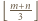 . Ponadto w każdej linii mogą pojawić się co najwyżej dwie wieże. Łącząc powyższe obserwacje, uzyskujemy, że liczba wież nie przekracza
. Ponadto w każdej linii mogą pojawić się co najwyżej dwie wieże. Łącząc powyższe obserwacje, uzyskujemy, że liczba wież nie przekracza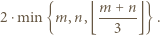
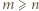 oraz, że
oraz, że 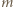 to liczba kolumn, a
to liczba kolumn, a  - liczba wierszy. Nietrudno wskazać przykład, że jeśli
- liczba wierszy. Nietrudno wskazać przykład, że jeśli 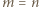 , to można osiągnąć ustawienie
, to można osiągnąć ustawienie 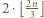 wież. Jeżeli
wież. Jeżeli 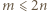 , to w
, to w 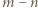 wierszach umieszczamy po dwie wieże, tym samym redukując szachownicę do kwadratu o boku
wierszach umieszczamy po dwie wieże, tym samym redukując szachownicę do kwadratu o boku 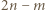 i wobec obserwacji z poprzedniego zdania, znów otrzymujemy ustawienie realizujące
i wobec obserwacji z poprzedniego zdania, znów otrzymujemy ustawienie realizujące 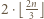 wież. Wreszcie dla
wież. Wreszcie dla 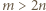 ustawiamy po dwie wieże w każdym wierszu i otrzymujemy ustawienie
ustawiamy po dwie wieże w każdym wierszu i otrzymujemy ustawienie 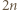 wież.
wież.