Przyporządkujmy polom szachownicy w naturalny sposób pary liczb całkowitych 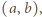 gdzie
gdzie 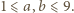 Pomalujmy pola o obu współrzędnych parzystych na niebiesko, pola o obu współrzędnych nieparzystych - na czerwono, a pozostałe pola - na żółto.
Pomalujmy pola o obu współrzędnych parzystych na niebiesko, pola o obu współrzędnych nieparzystych - na czerwono, a pozostałe pola - na żółto.
Przypuśćmy, że pionki mogą poruszać się dowolnie długo w taki sposób, by żadne dwa nie spotkały się na jednym polu. W takim razie w każdej chwili na 16 niebieskich polach może znajdować się co najwyżej 16 pionków. Każdy pionek z czerwonego pola znajdzie się po dwóch ruchach na niebieskim polu, więc na czerwonych polach może przebywać w każdej chwili również co najwyżej 16 pionków. Ponadto każdy pionek z żółtego pola po jednym ruchu znajdzie się na polu niebieskim lub czerwonym. W takim razie na żółtych polach mogą przebywać naraz co najwyżej 32 pionki. Stąd na szachownicy mogą być łącznie najwyżej 64 pionki.
Jeśli pionków jest 65, to po pewnym czasie dwa z nich muszą znaleźć się na jednym polu.
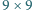 umieszczono 65 pionków, każdy na innym polu. Co minutę każdy pionek wykonuje ruch na pole sąsiadujące bokiem z polem, na którym się znajduje, w taki sposób, że każde kolejne dwa ruchy pionka mają prostopadłe kierunki. Wykazać, że po pewnym czasie dwa pionki znajdą się na jednym polu.
umieszczono 65 pionków, każdy na innym polu. Co minutę każdy pionek wykonuje ruch na pole sąsiadujące bokiem z polem, na którym się znajduje, w taki sposób, że każde kolejne dwa ruchy pionka mają prostopadłe kierunki. Wykazać, że po pewnym czasie dwa pionki znajdą się na jednym polu.
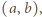 gdzie
gdzie 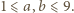 Pomalujmy pola o obu współrzędnych parzystych na niebiesko, pola o obu współrzędnych nieparzystych - na czerwono, a pozostałe pola - na żółto.
Pomalujmy pola o obu współrzędnych parzystych na niebiesko, pola o obu współrzędnych nieparzystych - na czerwono, a pozostałe pola - na żółto.