Zadania z matematyki - I 2020»Zadanie 1625
o zadaniu...
- Zadanie pochodzi z artykułu Zadania z matematyki - I 2020
- Publikacja w Delcie: styczeń 2020
- Publikacja elektroniczna: 31 sierpnia 2020
Znaleźć największą liczbę parami różnych punktów kratowych 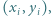
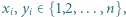 spośród których nie można wybrać czterech wierzchołków równoległoboku.
spośród których nie można wybrać czterech wierzchołków równoległoboku.

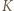 będzie zbiorem punktów o współrzędnych należących do zbioru
będzie zbiorem punktów o współrzędnych należących do zbioru 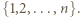 Niech
Niech 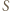 będzie zbiorem punktów należących do
będzie zbiorem punktów należących do 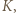 których co najmniej jedna współrzędna jest równa 1. Wówczas w
których co najmniej jedna współrzędna jest równa 1. Wówczas w 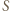 nie ma 4 punktów będących wierzchołkami równoległoboku, zatem szukana liczba nie przekracza liczności
nie ma 4 punktów będących wierzchołkami równoległoboku, zatem szukana liczba nie przekracza liczności 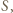 czyli
czyli 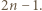
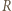 zbioru
zbioru 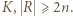 Przypuśćmy, że w
Przypuśćmy, że w 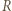 nie ma 4 wierzchołków równoległoboku. Dla
nie ma 4 wierzchołków równoległoboku. Dla 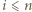 niech
niech 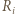 będzie zbiorem punktów należących do
będzie zbiorem punktów należących do 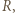 których pierwsza współrzędna wynosi
których pierwsza współrzędna wynosi 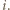 Niech
Niech 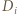 będzie zbiorem odległości "najniższego" punktu zbioru
będzie zbiorem odległości "najniższego" punktu zbioru 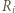 od pozostałych punktów tego zbioru. Wówczas
od pozostałych punktów tego zbioru. Wówczas 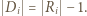 Ponadto, ze względu na przypuszczenie o braku równoległoboku, zbiory
Ponadto, ze względu na przypuszczenie o braku równoległoboku, zbiory 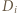 muszą być parami rozłączne, a zatem
muszą być parami rozłączne, a zatem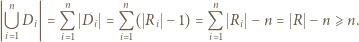
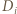 jest podzbiorem
jest podzbiorem 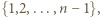 więc lewa strona powyższej nierówności nie może przekraczać
więc lewa strona powyższej nierówności nie może przekraczać 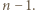 Wobec przedstawionych rozważań odpowiedzią na pytanie z zadania jest
Wobec przedstawionych rozważań odpowiedzią na pytanie z zadania jest