Zadanie ZM-1591
o zadaniu...
- Publikacja w Delcie: luty 2019
- Publikacja elektroniczna: 1 lutego 2019
Na okręgu wyróżniono  punktów białych oraz
punktów białych oraz 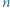 punktów czarnych. Białe punkty są ponumerowane liczbami od 1 do
punktów czarnych. Białe punkty są ponumerowane liczbami od 1 do 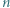 zgodnie z ruchem wskazówek zegara, a czarne punkty są ponumerowane liczbami od 1 do
zgodnie z ruchem wskazówek zegara, a czarne punkty są ponumerowane liczbami od 1 do 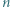 przeciwnie do ruchu wskazówek zegara. Wykazać, że ten okrąg można rozciąć na dwa łuki o tej własności, że każdy numer od 1 do
przeciwnie do ruchu wskazówek zegara. Wykazać, że ten okrąg można rozciąć na dwa łuki o tej własności, że każdy numer od 1 do 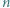 pojawia się dokładnie raz na każdym z nich.
pojawia się dokładnie raz na każdym z nich.


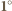 Pomiędzy punktami o numerze 1 znajdują się punkty białe o numerach od 2 do
Pomiędzy punktami o numerze 1 znajdują się punkty białe o numerach od 2 do 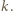 Wówczas wybierając jeden punkt podziału okręgu na łuki pomiędzy białymi punktami o numerach
Wówczas wybierając jeden punkt podziału okręgu na łuki pomiędzy białymi punktami o numerach 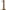 i
i 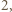 a drugi - w taki sposób, aby na obydwu uzyskanych łukach było po
a drugi - w taki sposób, aby na obydwu uzyskanych łukach było po  wyróżnionych punktów, uzyskujemy rozcięcie o postulowanej własności.
wyróżnionych punktów, uzyskujemy rozcięcie o postulowanej własności.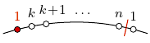
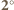 Pomiędzy punktami o numerze
Pomiędzy punktami o numerze 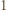 znajdują się punkty białe o numerach od
znajdują się punkty białe o numerach od 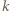 do
do 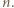 Wówczas wybierając jeden punkt podziału okręgu na łuki pomiędzy białymi punktami o numerach
Wówczas wybierając jeden punkt podziału okręgu na łuki pomiędzy białymi punktami o numerach 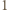 i
i 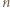 (a drugi odpowiednio jak wyżej), uzyskujemy rozcięcie spełniające warunki zadania.
(a drugi odpowiednio jak wyżej), uzyskujemy rozcięcie spełniające warunki zadania.