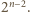Zadanie ZM-1538
o zadaniu...
- Publikacja w Delcie: sierpień 2017
- Publikacja elektroniczna: 30 lipca 2017
Niech 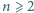 będzie liczbą całkowitą. Znaleźć liczbę przedstawień liczby
będzie liczbą całkowitą. Znaleźć liczbę przedstawień liczby 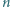 w postaci sumy pewnej liczby dodatnich całkowitych składników, pośród których jest parzysta liczba liczb parzystych.
w postaci sumy pewnej liczby dodatnich całkowitych składników, pośród których jest parzysta liczba liczb parzystych.

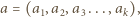
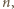 nazwiemy kompozycją liczby
nazwiemy kompozycją liczby 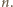
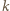 -elementowe kompozycje liczby
-elementowe kompozycje liczby 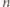 pozostają we wzajemnie jednoznacznej odpowiedniości z
pozostają we wzajemnie jednoznacznej odpowiedniości z 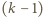 -elementowymi podzbiorami zbioru
-elementowymi podzbiorami zbioru 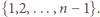 Każdej takiej kompozycji
Każdej takiej kompozycji 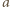 możemy przypisać zbiór
możemy przypisać zbiór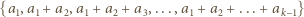
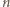 jest równa liczbie podzbiorów zbioru
jest równa liczbie podzbiorów zbioru 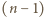 -elementowego, czyli
-elementowego, czyli 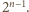
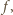 która przyporządkowuje każdej kompozycji
która przyporządkowuje każdej kompozycji  liczby
liczby 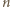 pewną kompozycję następująco: jeżeli
pewną kompozycję następująco: jeżeli 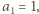 to
to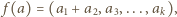
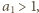 to
to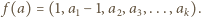
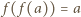 dla każdej kompozycji
dla każdej kompozycji 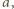 więc
więc 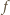 zadaje podział zbioru wszystkich kompozycji liczby
zadaje podział zbioru wszystkich kompozycji liczby 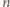 na pary. Wprost z definicji
na pary. Wprost z definicji 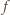 wynika, że kompozycje w obrębie każdej pary różnią się parzystością liczby parzystych wyrazów. To oznacza, że liczba kompozycji zawierających parzystą liczbę liczb parzystych jest równa połowie liczby wszystkich kompozycji, czyli
wynika, że kompozycje w obrębie każdej pary różnią się parzystością liczby parzystych wyrazów. To oznacza, że liczba kompozycji zawierających parzystą liczbę liczb parzystych jest równa połowie liczby wszystkich kompozycji, czyli