Interpretacja kombinatoryczna»Zadanie 2
o zadaniu...
- Zadanie pochodzi z artykułu Interpretacja kombinatoryczna
- Publikacja w Delcie: kwiecień 2017
- Publikacja elektroniczna: 30 marca 2017
Udowodnij tożsamość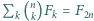 
( 
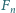oznacza 
-tą liczbę Fibonacciego, czyli rozwiązanie równania rekurencyjnego 
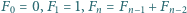dla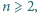 
a zarazem liczbę pokryć paska 
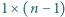kwadratami 
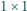i prostokątami 
).
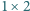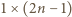kwadratami 
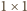i prostokątami 
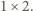Każde takie pokrycie musi zawierać co najmniej 
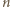elementów, w tym co najmniej jeden kwadrat. Jeśli w pokryciu wśród pierwszych 
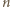elementów jest dokładnie 
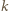kwadratów (i 
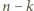prostokątów 
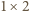), to można je rozmieścić na 
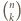sposobów i pokrywają one w sumie prostokąt 
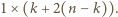Pozostały fragment paska 
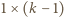można pokryć na 
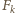sposobów. Tę drugą interpretację opisuje lewa strona tożsamości, stąd teza.