- Narzędzia
- Obiekty
- Słowa kluczowe
- Kategoria
- Kombinatoryka
Zadanie ZM-1596
o zadaniu...
- Publikacja w Delcie: marzec 2019
- Publikacja elektroniczna: 1 marca 2019
Definicje
Przez n-turniej będziemy rozumieli układ rozgrywek, w którym każda para spośród 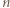 zawodników
zawodników 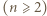 rozegrała dokładnie jeden mecz i nie było remisów.
rozegrała dokładnie jeden mecz i nie było remisów.
owiemy, że zawodnik 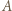 jest mistrzem, jeśli dla każdego zawodnika
jest mistrzem, jeśli dla każdego zawodnika 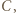 z którym
z którym 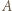 przegrał, istnieje zawodnik
przegrał, istnieje zawodnik 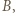 który przegrał z
który przegrał z 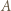 i wygrał z
i wygrał z 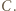 Innymi słowy, mistrz to zawodnik, który wygrał z każdym innym bezpośrednio lub pośrednio.
Innymi słowy, mistrz to zawodnik, który wygrał z każdym innym bezpośrednio lub pośrednio.
Wyznaczyć wszystkie 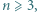 dla których istnieje
dla których istnieje 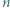 -turniej, w którym każdy jest mistrzem.
-turniej, w którym każdy jest mistrzem.
Rozwiązanie
Odpowiedź. 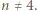
Nazwijmy mistrzowskim taki  -turniej, w którym każdy jest mistrzem. Udowodnimy, że jeśli istnieje mistrzowski
-turniej, w którym każdy jest mistrzem. Udowodnimy, że jeśli istnieje mistrzowski  -turniej, to istnieje mistrzowski
-turniej, to istnieje mistrzowski 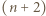 -turniej.
-turniej.
Niech 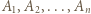 będą zawodnikami pewnego mistrzowskiego
będą zawodnikami pewnego mistrzowskiego 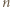 -turnieju, a
-turnieju, a 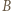 i
i 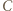 takimi dwoma dodatkowymi zawodnikami, że
takimi dwoma dodatkowymi zawodnikami, że 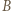 wygrał z
wygrał z 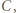 a ponadto
a ponadto 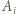 wygrał z
wygrał z 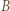 i przegrał z
i przegrał z 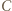 dla każdego
dla każdego 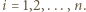 Wówczas
Wówczas 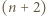 -turniej powstały przez dołączenie zawodników
-turniej powstały przez dołączenie zawodników 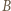 i
i 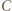 jest mistrzowski.
jest mistrzowski.
Nietrudno sprawdzić, że 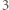 -turniej złożony z zawodników
-turniej złożony z zawodników 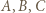 takich, że
takich, że 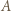 wygrał z
wygrał z 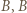 wygrał z
wygrał z 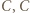 wygrał z
wygrał z 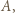 oraz
oraz 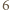 -turniej pokazany na poniższym rysunku (punkty oznaczają zawodników, a strzałka z
-turniej pokazany na poniższym rysunku (punkty oznaczają zawodników, a strzałka z 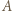 do
do 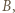 że
że 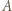 wygrał z
wygrał z 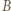 ) są mistrzowskie. W połączeniu z konkluzją poprzednich dwóch akapitów prowadzi to do wniosku, że
) są mistrzowskie. W połączeniu z konkluzją poprzednich dwóch akapitów prowadzi to do wniosku, że  -turniej mistrzowski istnieje dla każdej liczby nieparzystej
-turniej mistrzowski istnieje dla każdej liczby nieparzystej 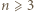 oraz dla każdej liczby parzystej
oraz dla każdej liczby parzystej 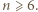
Pozostaje udowodnić, że nie istnieje mistrzowski 4-turniej. Przypuśćmy, że jednak istnieje, i oznaczmy zawodników przez 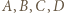 w taki sposób, że
w taki sposób, że 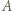 wygrał z
wygrał z 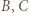 wygrał z
wygrał z 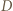 oraz (bez straty ogólności)
oraz (bez straty ogólności) 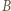 wygrał z
wygrał z 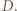 Wówczas, skoro
Wówczas, skoro 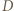 jest mistrzem, to
jest mistrzem, to 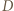 musiał pośrednio wygrać z
musiał pośrednio wygrać z 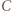 - jedyna możliwość jest taka, że
- jedyna możliwość jest taka, że 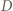 wygrał z
wygrał z 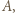 a
a 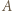 wygrał z
wygrał z 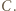 Jednak wówczas ten z zawodników
Jednak wówczas ten z zawodników 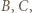 który przegrał mecz między nimi, nie miał jak wygrać pośrednio z tym drugim - sprzeczność.
który przegrał mecz między nimi, nie miał jak wygrać pośrednio z tym drugim - sprzeczność.
