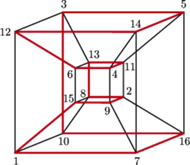
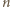Każdy podzbiór -elementowego zbioru 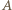można opisać ciągiem 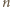zer i jedynek, gdzie 1 na 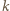-tym miejscu oznacza, że 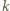-ty element zbioru 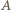należy do rozważanego podzbioru, a 0 - że nie należy. Wtedy podzbiory 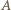to wierzchołki 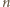-wymiarowego hipersześcianu, przy czym podzbiory różniące się jednym elementem połączone są krawędzią.

Szukany ciąg można wyznaczyć przez cykl Hamiltona na tym hipersześcianie, podobnie jak na rysunku (ostatni i pierwszy podzbiór w takim ciągu też różnią się jednym elementem).