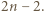Klub 44M - zadania I 2019»Zadanie 773
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania I 2019
- Publikacja w Delcie: styczeń 2019
- Publikacja elektroniczna: 31 grudnia 2018
- Artykuł źródłowy w wersji do druku [application/pdf]: (388 KB)
Dana jest liczba nieparzysta 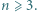 W każde pole kwadratowej planszy
W każde pole kwadratowej planszy 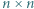 wpisujemy jedną z liczb
wpisujemy jedną z liczb 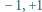 tak, że suma wszystkich wpisanych liczb wynosi 1. Wyznaczamy sumę liczb w każdym wierszu oraz sumę liczb w każdej kolumnie; dostajemy ciąg
tak, że suma wszystkich wpisanych liczb wynosi 1. Wyznaczamy sumę liczb w każdym wierszu oraz sumę liczb w każdej kolumnie; dostajemy ciąg 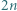 liczb nieparzystych. Ile maksymalnie może być w tym ciągu liczb ujemnych?
liczb nieparzystych. Ile maksymalnie może być w tym ciągu liczb ujemnych?

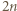 sum (wierszy i kolumn) może więc być co najwyżej
sum (wierszy i kolumn) może więc być co najwyżej 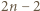 liczb ujemnych.
liczb ujemnych.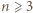 ta wartość jest osiągalna. Ilustracja przedstawia przykładową realizację, gdy
ta wartość jest osiągalna. Ilustracja przedstawia przykładową realizację, gdy 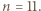 Opis algorytmu: cały skrajny dolny wiersz oraz całą skrajną prawą kolumnę wypełniamy jedynkami. Po odcięciu tego fragmentu zostaje plansza kwadratowa o boku długości parzystej
Opis algorytmu: cały skrajny dolny wiersz oraz całą skrajną prawą kolumnę wypełniamy jedynkami. Po odcięciu tego fragmentu zostaje plansza kwadratowa o boku długości parzystej 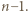 W jej górnym wierszu umieszczamy, kolejno od lewej,
W jej górnym wierszu umieszczamy, kolejno od lewej, 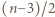 jedynek oraz
jedynek oraz 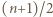 minus jedynek. W kolejnych wierszach (planszy
minus jedynek. W kolejnych wierszach (planszy 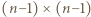 ) powtarzamy ten układ z przesunięciem (w każdym kroku) o jednostkę w prawo; nadwyżkę wychodzącą poza prawy skraj przenosimy przy tym cyklicznie na skrajne lewe pole.
) powtarzamy ten układ z przesunięciem (w każdym kroku) o jednostkę w prawo; nadwyżkę wychodzącą poza prawy skraj przenosimy przy tym cyklicznie na skrajne lewe pole.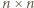 uzyskujemy przewagę minusów nad plusami we wszystkich wierszach i kolumnach z wyjątkiem ostatniego i ostatniej. Każdy z początkowych
uzyskujemy przewagę minusów nad plusami we wszystkich wierszach i kolumnach z wyjątkiem ostatniego i ostatniej. Każdy z początkowych 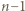 wierszy ma sumę
wierszy ma sumę 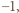 zaś ostatni wiersz ma sumę
zaś ostatni wiersz ma sumę 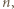 zatem suma całej tabeli wynosi 1. Stąd, ostatecznie, odpowiedź: szukane maksimum wynosi
zatem suma całej tabeli wynosi 1. Stąd, ostatecznie, odpowiedź: szukane maksimum wynosi