Klub 44M - zadania VI 2017»Zadanie 744
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania VI 2017
- Publikacja w Delcie: czerwiec 2017
- Publikacja elektroniczna: 31 maja 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (90 KB)
-
Zadanie 744 zostało opracowane na podstawie propozycji, którą przysłał pan Paweł Kubit z Krakowa.
Dana jest liczba całkowita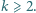 
Niech 
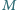będzie takim zbiorem dodatnich liczb całkowitych, że dla każdej pary różnych liczb 
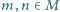zachodzi nierówność 
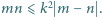Wykazać, że zbiorze 
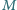jest nie więcej niż 
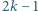liczb. Czy dla każdej liczby 
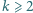istnieje 
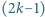-elementowy zbiór 
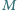o podanej własności?
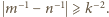Niech 
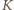będzie zbiorem odwrotności wszystkich liczb za zbioru 
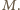Dowolne dwa elementy zbioru 
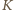są więc oddalone o co najmniej 
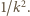Zatem w każdym spośród 
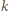przedziałów![(0, 1-], (-1,-2-], ( 2-,-3] ,...,( k-−1, k-] k2 k2 k2 k2 k2 k2 k2](/math/temat/matematyka/kombinatoryka/zadania/2017/05/29/zm-k44-744/7x-d28462c3f0c14c690f4776454216c605e7515ddb-dm-66,57,43-FF,FF,FF.gif)
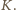Pozostałe liczby dodatnie tworzą przedział 
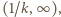w którym są jedynie odwrotności liczb naturalnych 
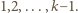To pokazuje, że zbiór 
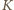(więc i zbiór 
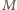) może liczyć co najwyżej 
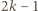elementów.
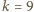nie istnieje 
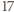-elementowy zbiór 
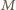o podanej własności. Jak w przypadku ogólnym, zauważamy, że w każdym z przedziałów ![|(0, 181] ,( 181,821],(821, 381]](/math/temat/matematyka/kombinatoryka/zadania/2017/05/29/zm-k44-744/4x-6cac8931e3035b7a31fa43086bacf339c85f8ab3-im-66,57,43-FF,FF,FF.gif)
może być tylko jeden element zbioru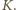 
Dalej, odwrotności liczb naturalnych, leżące w przedziale ![(-1, 1] , 27 9](/math/temat/matematyka/kombinatoryka/zadania/2017/05/29/zm-k44-744/6x-6cac8931e3035b7a31fa43086bacf339c85f8ab3-im-66,57,43-FF,FF,FF.gif)
rozbijamy na pięć podzbiorów: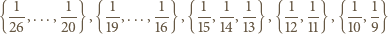
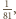więc zawiera co najwyżej jeden element zbioru 
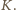No i zostają jeszcze ułamki 
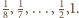Liczność zbioru 
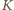(więc i 
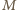) nie przekracza 
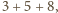czyli 16.