Aby udowodnić równoważność, wykażemy osobno dwie implikacje.
Ponumerujmy osoby obecne na przyjęciu liczbami od 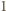 do
do  oraz oznaczmy liczbę wszystkich powitań przez
oraz oznaczmy liczbę wszystkich powitań przez 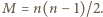 Niech
Niech 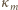 będzie permutacją zbioru
będzie permutacją zbioru 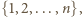 która liczbie
która liczbie 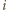 przyporządkowuje numer osoby, mającej na głowie kapelusz
przyporządkowuje numer osoby, mającej na głowie kapelusz 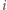 -tej osoby po
-tej osoby po  -tym powitaniu. Mamy więc
-tym powitaniu. Mamy więc 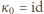 oraz
oraz 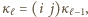 gdzie
gdzie 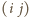 jest transpozycją, a
jest transpozycją, a 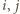 to numery osób uczestniczących w
to numery osób uczestniczących w 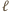 -tym powitaniu.
-tym powitaniu.
Wobec tego 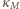 jest iloczynem
jest iloczynem 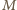 transpozycji (wszystkich możliwych par elementów zbioru
transpozycji (wszystkich możliwych par elementów zbioru 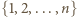 ). Z drugiej strony, w myśl warunków zadania,
). Z drugiej strony, w myśl warunków zadania, 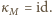 Ponieważ identyczność jest permutacją parzystą, więc wynika z tego, że
Ponieważ identyczność jest permutacją parzystą, więc wynika z tego, że 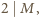 skąd uzyskujemy
skąd uzyskujemy 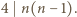 To oznacza, że jeżeli opisana sytuacja jest możliwa, to
To oznacza, że jeżeli opisana sytuacja jest możliwa, to 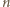 daje resztę 0 lub 1 przy dzieleniu przez 4.
daje resztę 0 lub 1 przy dzieleniu przez 4.
Aby uzasadnić, że dla każdego 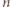 dającego resztę 0 lub 1 przy dzieleniu przez 4 istnieje kolejność powitań prowadząca do opisanej w treści zadania sytuacji, przeprowadzimy dowód indukcyjny.
dającego resztę 0 lub 1 przy dzieleniu przez 4 istnieje kolejność powitań prowadząca do opisanej w treści zadania sytuacji, przeprowadzimy dowód indukcyjny.
Jeżeli 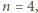 to bezpośrednio sprawdzamy, że
to bezpośrednio sprawdzamy, że
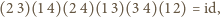
więc wystarczy, że najpierw przywitają się osoby 1 i 2, potem 3 i 4 itd.
Przypuśćmy, że dla pewnego 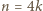 mamy odpowiednią kolejność powitań, czyli odpowiedni iloczyn transpozycji. Aby uzyskać odpowiednią kolejność dla
mamy odpowiednią kolejność powitań, czyli odpowiedni iloczyn transpozycji. Aby uzyskać odpowiednią kolejność dla 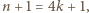 dokonajmy następujących zmian w tym iloczynie:
dokonajmy następujących zmian w tym iloczynie:
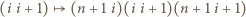
dla 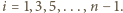 W ten sposób uzupełniliśmy iloczyn o
W ten sposób uzupełniliśmy iloczyn o 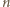 transpozycji (odpowiadających powitaniom z "nową" osobą numer
transpozycji (odpowiadających powitaniom z "nową" osobą numer 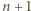 ) i łatwo sprawdzić, że warunki zadania dla nowej kolejności są spełnione.
) i łatwo sprawdzić, że warunki zadania dla nowej kolejności są spełnione.
Z kolei aby uzyskać odpowiednią kolejność dla 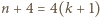 osób, dokonujemy podobnych zmian:
osób, dokonujemy podobnych zmian:
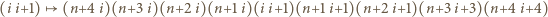
dla 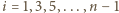 oraz dołączamy (w dowolnym miejscu) zestaw sześciu kolejno po sobie następujących powitań czterech nowych osób:
oraz dołączamy (w dowolnym miejscu) zestaw sześciu kolejno po sobie następujących powitań czterech nowych osób:
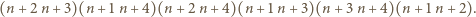
W ten sposób rozszerzyliśmy kolejność powitań w taki sposób, że znów po nastąpieniu wszystkich każdy ma znów swój kapelusz przy 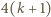 osobach. To kończy dowód indukcyjny.
osobach. To kończy dowód indukcyjny.
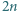 miast. Między niektórymi parami miast istnieją dwukierunkowe połączenia lotnicze, których w sumie jest
miast. Między niektórymi parami miast istnieją dwukierunkowe połączenia lotnicze, których w sumie jest 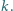 Ceny biletów na różnych odcinkach są różne, ale na każdym odcinku cena jest taka sama niezależnie od kierunku lotu. Wyznaczyć najmniejszą stałą
Ceny biletów na różnych odcinkach są różne, ale na każdym odcinku cena jest taka sama niezależnie od kierunku lotu. Wyznaczyć najmniejszą stałą  (niezależną od
(niezależną od 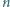 i
i 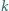 ) o tej własności, że zawsze można tak zaplanować podróż złożoną z co najmniej
) o tej własności, że zawsze można tak zaplanować podróż złożoną z co najmniej 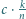 przelotów, aby każdy kolejny lot był droższy od poprzedniego.
przelotów, aby każdy kolejny lot był droższy od poprzedniego.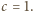
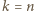 i wszystkie połączenia są realizowane między rozłącznymi parami miast, to każda podróż może być złożona z tylko jednego lotu. Stąd
i wszystkie połączenia są realizowane między rozłącznymi parami miast, to każda podróż może być złożona z tylko jednego lotu. Stąd 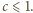
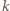 dni. W każdym z miast umieśćmy na początku jednego turystę. Pierwszego dnia zaplanujmy loty pary turystów, którzy znajdują się w miastach, między którymi kursuje najtańszy lot; drugiego dnia - pary turystów, którzy znajdują się w miastach, między którymi jest drugi najtańszy lot itd.
dni. W każdym z miast umieśćmy na początku jednego turystę. Pierwszego dnia zaplanujmy loty pary turystów, którzy znajdują się w miastach, między którymi kursuje najtańszy lot; drugiego dnia - pary turystów, którzy znajdują się w miastach, między którymi jest drugi najtańszy lot itd.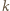 dniach każdy turysta będzie już po podróży mającej tę własność, że każdy kolejny lot był droższy od poprzedniego. Ponadto łącznie wszyscy turyści wykonają w sumie
dniach każdy turysta będzie już po podróży mającej tę własność, że każdy kolejny lot był droższy od poprzedniego. Ponadto łącznie wszyscy turyści wykonają w sumie 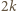 lotów, gdyż każdego dnia dokładnie dwóch wsiadło do samolotu. Stąd wniosek, że średnia długość podróży wśród wszystkich turystów jest równa
lotów, gdyż każdego dnia dokładnie dwóch wsiadło do samolotu. Stąd wniosek, że średnia długość podróży wśród wszystkich turystów jest równa 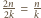 lotów. W związku z tym istnieje turysta, którego wycieczka jest złożona z co najmniej tylu lotów, a zatem
lotów. W związku z tym istnieje turysta, którego wycieczka jest złożona z co najmniej tylu lotów, a zatem 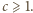
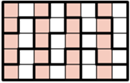
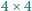 należy wpisać pewną liczbę całkowitą w taki sposób, aby sumy liczb w każdej kolumnie i w każdym wierszu były potęgami liczby 2 o wykładniku całkowitym nieujemnym. Czy można to zrobić w taki sposób, aby każde dwie z tych ośmiu sum były różne?
należy wpisać pewną liczbę całkowitą w taki sposób, aby sumy liczb w każdej kolumnie i w każdym wierszu były potęgami liczby 2 o wykładniku całkowitym nieujemnym. Czy można to zrobić w taki sposób, aby każde dwie z tych ośmiu sum były różne?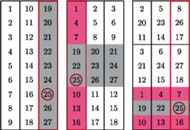
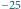
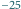
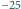
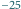
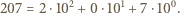
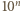 wymagają najwyżej
wymagają najwyżej  cyfr.
cyfr.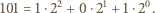
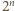 wymagają najwyżej
wymagają najwyżej 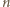 cyfr.
cyfr. o następującej własności: dla każdego pokolorowania dokładnie
o następującej własności: dla każdego pokolorowania dokładnie  pól tablicy o wymiarach
pól tablicy o wymiarach 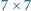 na czarno istnieje kwadrat
na czarno istnieje kwadrat 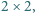 który zawiera co najmniej trzy czarne pola.
który zawiera co najmniej trzy czarne pola.

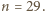
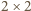 zawiera co najwyżej dwa czarne pola. Wówczas każdy z
zawiera co najwyżej dwa czarne pola. Wówczas każdy z 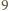 białych kwadratów
białych kwadratów 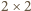 oraz każda z
oraz każda z 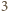 szarych figur o polu
szarych figur o polu 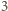 na pierwszym rysunku zawiera co najwyżej
na pierwszym rysunku zawiera co najwyżej 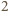 czarne pola, a ponadto każdy z
czarne pola, a ponadto każdy z 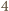 kolorowych kwadratów jednostkowych może być czarny. To oznacza, że łącznie w tablicy jest co najwyżej
kolorowych kwadratów jednostkowych może być czarny. To oznacza, że łącznie w tablicy jest co najwyżej 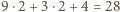 czarnych pól.
czarnych pól.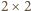 zawiera dokładnie dwa czarne pola. To oznacza, że szukana najmniejsza wartość
zawiera dokładnie dwa czarne pola. To oznacza, że szukana najmniejsza wartość 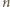 jest równa 29.
jest równa 29.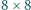 wpisać liczby
wpisać liczby 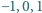 (w każde pole jedną liczbę) tak, by sumy liczb w wierszach oraz sumy liczb w kolumnach utworzyły układ 16 różnych wartości? Czy odpowiedź zmieni się, gdy będziemy rozważali tablicę
(w każde pole jedną liczbę) tak, by sumy liczb w wierszach oraz sumy liczb w kolumnach utworzyły układ 16 różnych wartości? Czy odpowiedź zmieni się, gdy będziemy rozważali tablicę 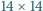 (i wymagali 28 różnych wartości)?
(i wymagali 28 różnych wartości)?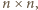 można utworzyć dla każdej liczby parzystej
można utworzyć dla każdej liczby parzystej  (więc i dla 8, i dla 14). Przykładowa konstrukcja:
(więc i dla 8, i dla 14). Przykładowa konstrukcja: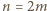 i niech
i niech 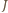 oznacza macierz
oznacza macierz 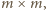 złożoną z samych jedynek, zaś
złożoną z samych jedynek, zaś 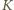 - macierz
- macierz 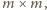 mającą jedynki na głównej przekątnej i nad nią, a poniżej przekątnej zera. Tworzymy macierz
mającą jedynki na głównej przekątnej i nad nią, a poniżej przekątnej zera. Tworzymy macierz 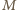 rozmiaru
rozmiaru 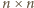 (o wyrazach
(o wyrazach 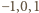 ):
):. M −JK−J](/math/temat/matematyka/kombinatoryka/zadania/2017/09/23/zm-k44-748/9x-807833042f4bcd6f5eb6f0d2f3609a7eb849fe84-dm-66,57,43-FF,FF,FF.gif)
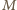 tworzą ciąg rosnący wszystkich liczb całkowitych od
tworzą ciąg rosnący wszystkich liczb całkowitych od 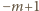 do
do 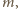 natomiast sumy liczb w kolejnych wierszach tworzą ciąg malejący wszystkich liczb całkowitych od
natomiast sumy liczb w kolejnych wierszach tworzą ciąg malejący wszystkich liczb całkowitych od 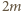 do
do 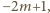 z pominięciem tych uzyskanych już jako sumy kolumn. Macierz
z pominięciem tych uzyskanych już jako sumy kolumn. Macierz 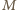 ma więc żądaną własność.
ma więc żądaną własność.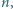 dla której istnieją czteroelementowe zbiory
dla której istnieją czteroelementowe zbiory 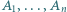 o następującej własności: każdy zbiór
o następującej własności: każdy zbiór 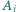 ma z każdym innym zbiorem
ma z każdym innym zbiorem 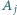 dokładnie jeden element wspólny, ale nie istnieje wspólny element wszystkich zbiorów
dokładnie jeden element wspólny, ale nie istnieje wspólny element wszystkich zbiorów 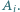
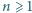 oraz pewien zbiór
oraz pewien zbiór 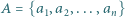 dodatnich liczb całkowitych. Na okręgu wyróżniono
dodatnich liczb całkowitych. Na okręgu wyróżniono 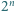 punktów i każdemu z nich przyporządkowano jedną z liczb ze zbioru
punktów i każdemu z nich przyporządkowano jedną z liczb ze zbioru 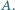 Udowodnić, że iloczyn liczb znajdujących się na pewnym łuku tego okręgu jest kwadratem liczby całkowitej.
Udowodnić, że iloczyn liczb znajdujących się na pewnym łuku tego okręgu jest kwadratem liczby całkowitej.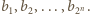 Dla każdej liczby
Dla każdej liczby 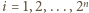 zdefiniujmy
zdefiniujmy 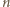 -wyrazowy ciąg binarny
-wyrazowy ciąg binarny 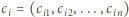 następująco:
następująco: 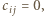 jeżeli pośród liczb
jeżeli pośród liczb 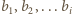 wartość
wartość 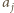 występuje parzystą liczbę razy oraz
występuje parzystą liczbę razy oraz 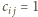 w przeciwnym przypadku.
w przeciwnym przypadku.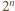 binarnych ciągów długości
binarnych ciągów długości 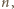 więc albo ciągi
więc albo ciągi 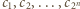 są parami różne i
są parami różne i 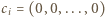 dla pewnego
dla pewnego 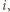 albo
albo 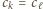 dla pewnych
dla pewnych 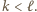 W pierwszym przypadku iloczyn liczb
W pierwszym przypadku iloczyn liczb 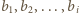 jest kwadratem liczby całkowitej, w drugim zaś - iloczyn liczb
jest kwadratem liczby całkowitej, w drugim zaś - iloczyn liczb 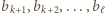 jest kwadratem liczby całkowitej.
jest kwadratem liczby całkowitej.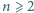 będzie liczbą całkowitą. Znaleźć liczbę przedstawień liczby
będzie liczbą całkowitą. Znaleźć liczbę przedstawień liczby 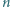 w postaci sumy pewnej liczby dodatnich całkowitych składników, pośród których jest parzysta liczba liczb parzystych.
w postaci sumy pewnej liczby dodatnich całkowitych składników, pośród których jest parzysta liczba liczb parzystych.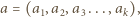
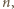 nazwiemy kompozycją liczby
nazwiemy kompozycją liczby 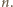
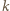 -elementowe kompozycje liczby
-elementowe kompozycje liczby 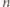 pozostają we wzajemnie jednoznacznej odpowiedniości z
pozostają we wzajemnie jednoznacznej odpowiedniości z 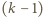 -elementowymi podzbiorami zbioru
-elementowymi podzbiorami zbioru 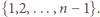 Każdej takiej kompozycji
Każdej takiej kompozycji 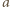 możemy przypisać zbiór
możemy przypisać zbiór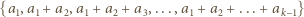
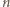 jest równa liczbie podzbiorów zbioru
jest równa liczbie podzbiorów zbioru 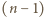 -elementowego, czyli
-elementowego, czyli 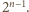
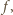 która przyporządkowuje każdej kompozycji
która przyporządkowuje każdej kompozycji  liczby
liczby 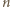 pewną kompozycję następująco: jeżeli
pewną kompozycję następująco: jeżeli 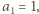 to
to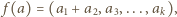
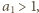 to
to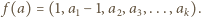
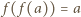 dla każdej kompozycji
dla każdej kompozycji 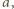 więc
więc 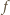 zadaje podział zbioru wszystkich kompozycji liczby
zadaje podział zbioru wszystkich kompozycji liczby 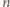 na pary. Wprost z definicji
na pary. Wprost z definicji 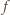 wynika, że kompozycje w obrębie każdej pary różnią się parzystością liczby parzystych wyrazów. To oznacza, że liczba kompozycji zawierających parzystą liczbę liczb parzystych jest równa połowie liczby wszystkich kompozycji, czyli
wynika, że kompozycje w obrębie każdej pary różnią się parzystością liczby parzystych wyrazów. To oznacza, że liczba kompozycji zawierających parzystą liczbę liczb parzystych jest równa połowie liczby wszystkich kompozycji, czyli 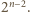
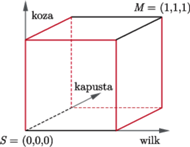
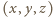 zer i jedynek oznaczających kolejno położenie wilka, kozy i kapusty: 0 - na pierwszym brzegu rzeki, 1 - na drugim. W przestrzeni trójki te to współrzędne wierzchołków sześcianu, przy czym wierzchołek
zer i jedynek oznaczających kolejno położenie wilka, kozy i kapusty: 0 - na pierwszym brzegu rzeki, 1 - na drugim. W przestrzeni trójki te to współrzędne wierzchołków sześcianu, przy czym wierzchołek 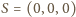 to położenie początkowe dobytku farmera, a
to położenie początkowe dobytku farmera, a 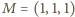 - docelowe.
- docelowe.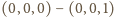 oznacza, że farmer pozostawił wilka z kozą bez opieki i wiezie kapustę, co skończy się źle dla kozy. Zadanie sprowadza się więc do połączenia punktów
oznacza, że farmer pozostawił wilka z kozą bez opieki i wiezie kapustę, co skończy się źle dla kozy. Zadanie sprowadza się więc do połączenia punktów 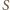 i
i 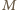 wzdłuż dobrych krawędzi, a to już łatwo zrobić na rysunku.
wzdłuż dobrych krawędzi, a to już łatwo zrobić na rysunku.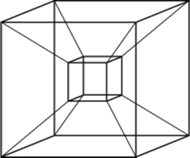
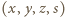 zer i jedynek, które tym razem są wierzchołkami czterowymiarowego hipersześcianu. Po usunięciu złych krawędzi łatwo znaleźć drogę od
zer i jedynek, które tym razem są wierzchołkami czterowymiarowego hipersześcianu. Po usunięciu złych krawędzi łatwo znaleźć drogę od 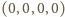 do
do 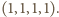
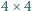 i wrócić do punktu wyjścia? (Pojedynczy skok konika to dwa pola w jedną stronę i jedno w kierunku prostopadłym.)
i wrócić do punktu wyjścia? (Pojedynczy skok konika to dwa pola w jedną stronę i jedno w kierunku prostopadłym.)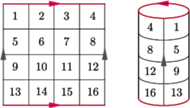
 zwinięto w rurkę i sklejono przeciwległe brzegi. Następnie sklejono końce tej rurki, uzyskując torus. Konik szachowy skacze po tym torusie zgodnie ze zwykłymi regułami opisanymi powyżej. Czy może on odwiedzić każde pole dokładnie raz i wrócić do punktu wyjścia?
zwinięto w rurkę i sklejono przeciwległe brzegi. Następnie sklejono końce tej rurki, uzyskując torus. Konik szachowy skacze po tym torusie zgodnie ze zwykłymi regułami opisanymi powyżej. Czy może on odwiedzić każde pole dokładnie raz i wrócić do punktu wyjścia?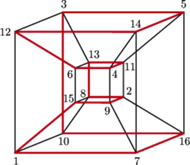
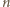 -wymiarowych, gdzie
-wymiarowych, gdzie 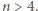
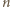 -elementowego zbioru
-elementowego zbioru 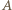 można opisać ciągiem
można opisać ciągiem 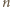 zer i jedynek, gdzie 1 na
zer i jedynek, gdzie 1 na 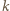 -tym miejscu oznacza, że
-tym miejscu oznacza, że 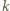 -ty element zbioru
-ty element zbioru 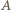 należy do rozważanego podzbioru, a 0 - że nie należy. Wtedy podzbiory
należy do rozważanego podzbioru, a 0 - że nie należy. Wtedy podzbiory 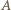 to wierzchołki
to wierzchołki 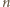 -wymiarowego hipersześcianu, przy czym podzbiory różniące się jednym elementem połączone są krawędzią.
-wymiarowego hipersześcianu, przy czym podzbiory różniące się jednym elementem połączone są krawędzią.
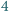 typu
typu 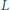 lub
lub 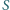 (rysunek) ułożono prostokąt. Wykazać, że liczba wykorzystanych płytek typu
(rysunek) ułożono prostokąt. Wykazać, że liczba wykorzystanych płytek typu 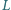 jest parzysta.
jest parzysta.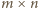 został ułożony z pewnej liczby opisanych płytek, to jego powierzchnia jest liczbą podzielną przez
został ułożony z pewnej liczby opisanych płytek, to jego powierzchnia jest liczbą podzielną przez 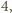 wobec czego co najmniej jeden z wymiarów jest liczbą podzielną przez
wobec czego co najmniej jeden z wymiarów jest liczbą podzielną przez 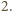 Przypuśćmy bez straty ogólności, że
Przypuśćmy bez straty ogólności, że 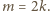

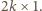
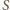 zawiera parzystą liczbę kolorowych pól (dokładnie dwa), a każda kostka typu
zawiera parzystą liczbę kolorowych pól (dokładnie dwa), a każda kostka typu 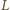 zawiera nieparzystą liczbę kolorowych pól (jedno lub trzy). Ponieważ liczba kolorowych pól w całym prostokącie jest parzysta (jako wielokrotność liczby
zawiera nieparzystą liczbę kolorowych pól (jedno lub trzy). Ponieważ liczba kolorowych pól w całym prostokącie jest parzysta (jako wielokrotność liczby 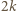 ), więc łączna liczba kostek zawierających nieparzystą liczbę kolorowych pól musi być parzysta.
), więc łączna liczba kostek zawierających nieparzystą liczbę kolorowych pól musi być parzysta.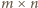 został ułożony z pewnej liczby opisanych płytek, to jego powierzchnia jest liczbą podzielną przez
został ułożony z pewnej liczby opisanych płytek, to jego powierzchnia jest liczbą podzielną przez 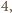 wobec czego co najmniej jeden z wymiarów jest liczbą podzielną przez
wobec czego co najmniej jeden z wymiarów jest liczbą podzielną przez 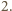 Przypuśćmy bez straty ogólności, że
Przypuśćmy bez straty ogólności, że 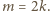
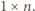
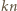 ), jak i w obrębie dowolnej płytki typu
), jak i w obrębie dowolnej płytki typu 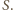 Tymczasem każda z płytek typu
Tymczasem każda z płytek typu 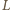 jest zdominowana przez pewien kolor (w stosunku pól
jest zdominowana przez pewien kolor (w stosunku pól 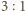 ). Wobec tego liczba płytek zdominowanych przez kolor biały musi być równa liczbie płytek zdominowanych przez kolor, a zatem łączna liczba płytek typu
). Wobec tego liczba płytek zdominowanych przez kolor biały musi być równa liczbie płytek zdominowanych przez kolor, a zatem łączna liczba płytek typu 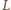 jest parzysta.
jest parzysta.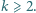 Niech
Niech 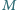 będzie takim zbiorem dodatnich liczb całkowitych, że dla każdej pary różnych liczb
będzie takim zbiorem dodatnich liczb całkowitych, że dla każdej pary różnych liczb 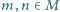 zachodzi nierówność
zachodzi nierówność 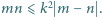 Wykazać, że zbiorze
Wykazać, że zbiorze 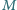 jest nie więcej niż
jest nie więcej niż 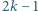 liczb. Czy dla każdej liczby
liczb. Czy dla każdej liczby 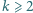 istnieje
istnieje 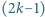 -elementowy zbiór
-elementowy zbiór 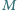 o podanej własności?
o podanej własności?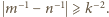 Niech
Niech 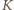 będzie zbiorem odwrotności wszystkich liczb za zbioru
będzie zbiorem odwrotności wszystkich liczb za zbioru 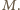 Dowolne dwa elementy zbioru
Dowolne dwa elementy zbioru 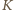 są więc oddalone o co najmniej
są więc oddalone o co najmniej 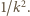 Zatem w każdym spośród
Zatem w każdym spośród 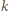 przedziałów
przedziałów![(0, 1-], (-1,-2-], ( 2-,-3] ,...,( k-−1, k-] k2 k2 k2 k2 k2 k2 k2](/math/temat/matematyka/kombinatoryka/zadania/2017/05/29/zm-k44-744/7x-d28462c3f0c14c690f4776454216c605e7515ddb-dm-66,57,43-FF,FF,FF.gif)
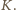 Pozostałe liczby dodatnie tworzą przedział
Pozostałe liczby dodatnie tworzą przedział 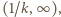 w którym są jedynie odwrotności liczb naturalnych
w którym są jedynie odwrotności liczb naturalnych 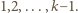 To pokazuje, że zbiór
To pokazuje, że zbiór 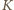 (więc i zbiór
(więc i zbiór 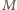 ) może liczyć co najwyżej
) może liczyć co najwyżej 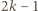 elementów.
elementów.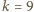 nie istnieje
nie istnieje 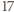 -elementowy zbiór
-elementowy zbiór 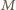 o podanej własności. Jak w przypadku ogólnym, zauważamy, że w każdym z przedziałów
o podanej własności. Jak w przypadku ogólnym, zauważamy, że w każdym z przedziałów ![|(0, 181] ,( 181,821],(821, 381]](/math/temat/matematyka/kombinatoryka/zadania/2017/05/29/zm-k44-744/4x-6cac8931e3035b7a31fa43086bacf339c85f8ab3-im-66,57,43-FF,FF,FF.gif) może być tylko jeden element zbioru
może być tylko jeden element zbioru 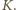 Dalej, odwrotności liczb naturalnych, leżące w przedziale
Dalej, odwrotności liczb naturalnych, leżące w przedziale ![(-1, 1] , 27 9](/math/temat/matematyka/kombinatoryka/zadania/2017/05/29/zm-k44-744/6x-6cac8931e3035b7a31fa43086bacf339c85f8ab3-im-66,57,43-FF,FF,FF.gif) rozbijamy na pięć podzbiorów:
rozbijamy na pięć podzbiorów: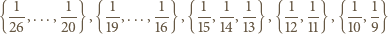
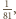 więc zawiera co najwyżej jeden element zbioru
więc zawiera co najwyżej jeden element zbioru 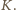 No i zostają jeszcze ułamki
No i zostają jeszcze ułamki 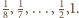 Liczność zbioru
Liczność zbioru 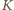 (więc i
(więc i 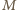 ) nie przekracza
) nie przekracza 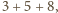 czyli 16.
czyli 16.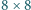 należy pomalować na czarno albo na biało. Na ile sposobów można uczynić to tak, aby każdy kwadrat
należy pomalować na czarno albo na biało. Na ile sposobów można uczynić to tak, aby każdy kwadrat 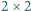 zawierał parzystą liczbę czarnych pól?
zawierał parzystą liczbę czarnych pól?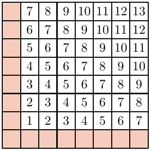
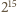 sposobów.
sposobów.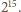
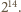
 osób w kapeluszach
osób w kapeluszach 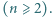 Następnie każde dwie osoby przywitały się dokładnie raz, przy czym każde powitanie polegało na zamianie kapeluszami, które w danej chwili witające się osoby miały na głowach. Okazało się, że po nastąpieniu wszystkich powitań każdy miał z powrotem swój kapelusz. Udowodnić, że taka sytuacja jest możliwa wtedy i tylko wtedy, gdy
Następnie każde dwie osoby przywitały się dokładnie raz, przy czym każde powitanie polegało na zamianie kapeluszami, które w danej chwili witające się osoby miały na głowach. Okazało się, że po nastąpieniu wszystkich powitań każdy miał z powrotem swój kapelusz. Udowodnić, że taka sytuacja jest możliwa wtedy i tylko wtedy, gdy 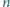 daje resztę 0 lub 1 przy dzieleniu przez 4.
daje resztę 0 lub 1 przy dzieleniu przez 4.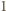 do
do  oraz oznaczmy liczbę wszystkich powitań przez
oraz oznaczmy liczbę wszystkich powitań przez 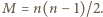 Niech
Niech 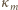 będzie permutacją zbioru
będzie permutacją zbioru 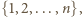 która liczbie
która liczbie 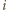 przyporządkowuje numer osoby, mającej na głowie kapelusz
przyporządkowuje numer osoby, mającej na głowie kapelusz 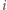 -tej osoby po
-tej osoby po  -tym powitaniu. Mamy więc
-tym powitaniu. Mamy więc 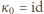 oraz
oraz 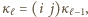 gdzie
gdzie 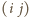 jest transpozycją, a
jest transpozycją, a 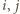 to numery osób uczestniczących w
to numery osób uczestniczących w 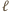 -tym powitaniu.
-tym powitaniu.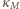 jest iloczynem
jest iloczynem 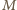 transpozycji (wszystkich możliwych par elementów zbioru
transpozycji (wszystkich możliwych par elementów zbioru 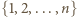 ). Z drugiej strony, w myśl warunków zadania,
). Z drugiej strony, w myśl warunków zadania, 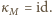 Ponieważ identyczność jest permutacją parzystą, więc wynika z tego, że
Ponieważ identyczność jest permutacją parzystą, więc wynika z tego, że 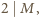 skąd uzyskujemy
skąd uzyskujemy 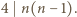 To oznacza, że jeżeli opisana sytuacja jest możliwa, to
To oznacza, że jeżeli opisana sytuacja jest możliwa, to 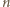 daje resztę 0 lub 1 przy dzieleniu przez 4.
daje resztę 0 lub 1 przy dzieleniu przez 4.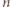 dającego resztę 0 lub 1 przy dzieleniu przez 4 istnieje kolejność powitań prowadząca do opisanej w treści zadania sytuacji, przeprowadzimy dowód indukcyjny.
dającego resztę 0 lub 1 przy dzieleniu przez 4 istnieje kolejność powitań prowadząca do opisanej w treści zadania sytuacji, przeprowadzimy dowód indukcyjny.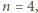 to bezpośrednio sprawdzamy, że
to bezpośrednio sprawdzamy, że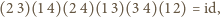
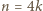 mamy odpowiednią kolejność powitań, czyli odpowiedni iloczyn transpozycji. Aby uzyskać odpowiednią kolejność dla
mamy odpowiednią kolejność powitań, czyli odpowiedni iloczyn transpozycji. Aby uzyskać odpowiednią kolejność dla 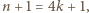 dokonajmy następujących zmian w tym iloczynie:
dokonajmy następujących zmian w tym iloczynie: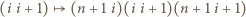
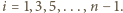 W ten sposób uzupełniliśmy iloczyn o
W ten sposób uzupełniliśmy iloczyn o 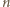 transpozycji (odpowiadających powitaniom z "nową" osobą numer
transpozycji (odpowiadających powitaniom z "nową" osobą numer 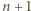 ) i łatwo sprawdzić, że warunki zadania dla nowej kolejności są spełnione.
) i łatwo sprawdzić, że warunki zadania dla nowej kolejności są spełnione.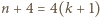 osób, dokonujemy podobnych zmian:
osób, dokonujemy podobnych zmian: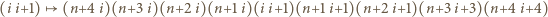
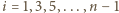 oraz dołączamy (w dowolnym miejscu) zestaw sześciu kolejno po sobie następujących powitań czterech nowych osób:
oraz dołączamy (w dowolnym miejscu) zestaw sześciu kolejno po sobie następujących powitań czterech nowych osób: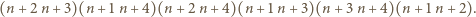
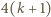 osobach. To kończy dowód indukcyjny.
osobach. To kończy dowód indukcyjny.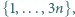 które nie zawierają dwóch liczb różniących się o
które nie zawierają dwóch liczb różniących się o 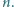
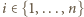 jest dokładnie pięć możliwości opisujących, które z liczb
jest dokładnie pięć możliwości opisujących, które z liczb 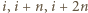 należą do podzbioru spełniającego warunek zadania. Mianowicie:
należą do podzbioru spełniającego warunek zadania. Mianowicie: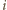 należy;
należy;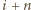 należy;
należy;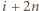 należy;
należy;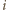 oraz
oraz 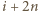 należą (natomiast
należą (natomiast 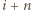 nie należy).
nie należy).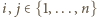 możliwości te są niezależne, to liczba szukanych pozdbiorów wynosi
możliwości te są niezależne, to liczba szukanych pozdbiorów wynosi 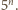
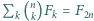 (
( 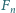 oznacza
oznacza  -tą liczbę Fibonacciego, czyli rozwiązanie równania rekurencyjnego
-tą liczbę Fibonacciego, czyli rozwiązanie równania rekurencyjnego 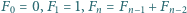 dla
dla 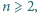 a zarazem liczbę pokryć paska
a zarazem liczbę pokryć paska 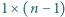 kwadratami
kwadratami 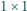 i prostokątami
i prostokątami 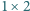 ).
).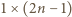 kwadratami
kwadratami 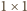 i prostokątami
i prostokątami 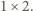 Każde takie pokrycie musi zawierać co najmniej
Każde takie pokrycie musi zawierać co najmniej 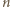 elementów, w tym co najmniej jeden kwadrat. Jeśli w pokryciu wśród pierwszych
elementów, w tym co najmniej jeden kwadrat. Jeśli w pokryciu wśród pierwszych 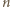 elementów jest dokładnie
elementów jest dokładnie 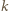 kwadratów (i
kwadratów (i 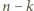 prostokątów
prostokątów 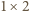 ), to można je rozmieścić na
), to można je rozmieścić na 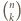 sposobów i pokrywają one w sumie prostokąt
sposobów i pokrywają one w sumie prostokąt 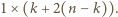 Pozostały fragment paska
Pozostały fragment paska 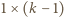 można pokryć na
można pokryć na 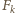 sposobów. Tę drugą interpretację opisuje lewa strona tożsamości, stąd teza.
sposobów. Tę drugą interpretację opisuje lewa strona tożsamości, stąd teza. Niech
Niech 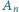 będzie liczbą takich słów, w których nie pojawia się blok
będzie liczbą takich słów, w których nie pojawia się blok 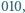 zaś
zaś 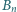 liczbą takich słów, w których w żadnym miejscu blok
liczbą takich słów, w których w żadnym miejscu blok 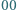 nie sąsiaduje z blokiem
nie sąsiaduje z blokiem 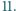 Dla każdej liczby naturalnej
Dla każdej liczby naturalnej 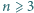 wyznaczyć wartość stosunku
wyznaczyć wartość stosunku 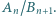
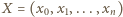 długości
długości 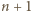 przyporządkujmy słowo
przyporządkujmy słowo 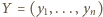 długości
długości 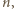 przyjmując
przyjmując 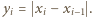 Znając słowo
Znając słowo 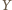 oraz element
oraz element 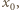 jednoznacznie odtwarzamy słowo
jednoznacznie odtwarzamy słowo 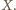
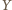 oznacza obecność bloku 0011 lub 1100 w słowie
oznacza obecność bloku 0011 lub 1100 w słowie 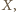 i na odwrót. Liczba słów
i na odwrót. Liczba słów 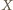 bez bloków 0011, 1100, z elementem początkowym
bez bloków 0011, 1100, z elementem początkowym 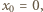 jest taka sama, jak tych z elementem początkowym
jest taka sama, jak tych z elementem początkowym 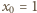 ; i jest, w myśl poprzedniego spostrzeżenia, taka sama, jak liczba słów
; i jest, w myśl poprzedniego spostrzeżenia, taka sama, jak liczba słów 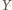 bez bloku 010. Stąd wniosek, że
bez bloku 010. Stąd wniosek, że 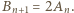
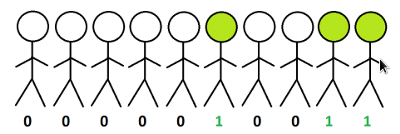
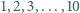 została wpisana na dziesięciu polach szachownicy
została wpisana na dziesięciu polach szachownicy 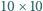 w taki sposób, że na każdym polu jest dokładnie jedna liczba. Wykazać, że istnieje wiersz lub kolumna tej szachownicy, w której występują co najmniej
w taki sposób, że na każdym polu jest dokładnie jedna liczba. Wykazać, że istnieje wiersz lub kolumna tej szachownicy, w której występują co najmniej 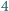 różne liczby.
różne liczby.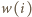 oraz
oraz 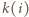 oznaczają odpowiednio liczbę wierszy i kolumn, zawierających liczbę
oznaczają odpowiednio liczbę wierszy i kolumn, zawierających liczbę 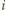 dla
dla 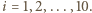 Ponieważ każda z dziesięciu liczb
Ponieważ każda z dziesięciu liczb 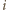 umieszczonych w tablicy leży na skrzyżowaniu jednego z
umieszczonych w tablicy leży na skrzyżowaniu jednego z 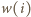 wierszy z jedną z
wierszy z jedną z 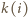 kolumn, to dla każdego
kolumn, to dla każdego 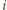 spełniona jest nierówność
spełniona jest nierówność 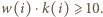 W takim razie również
W takim razie również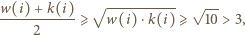
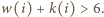
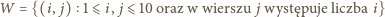
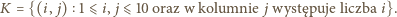
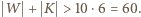 Bez straty ogólności przyjmijmy, że
Bez straty ogólności przyjmijmy, że 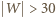 (przypadek
(przypadek 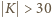 rozważa się analogicznie). Z zasady szufladkowej Dirichleta wiemy, że w takim razie dla pewnego
rozważa się analogicznie). Z zasady szufladkowej Dirichleta wiemy, że w takim razie dla pewnego 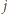 zbiór
zbiór 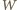 zawiera co najmniej
zawiera co najmniej 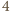 pary postaci
pary postaci 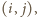 a to daje tezę.
a to daje tezę.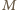 będzie zawodnikiem, który wygrał maksymalną liczbę meczów. Jeśli wygrał wszystkie, jest zwycięzcą. W przeciwnym wypadku istnieje zawodnik
będzie zawodnikiem, który wygrał maksymalną liczbę meczów. Jeśli wygrał wszystkie, jest zwycięzcą. W przeciwnym wypadku istnieje zawodnik 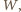 który wygrał z
który wygrał z 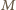 oraz istnieje przynajmniej jeden zawodnik pokonany przez
oraz istnieje przynajmniej jeden zawodnik pokonany przez 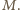
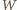 zwyciężył ze wszystkimi, którzy przegrali z
zwyciężył ze wszystkimi, którzy przegrali z 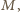 to
to 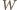 wygrałby więcej meczów niż
wygrałby więcej meczów niż 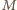 (bo pokonał też
(bo pokonał też 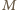 ) - sprzeczność. Zatem
) - sprzeczność. Zatem 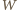 przegrał z którymś z graczy, z którymi wygrał
przegrał z którymś z graczy, z którymi wygrał 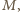 czyli istnieje trójkąt.
czyli istnieje trójkąt.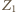 ; ustawmy go na początku rzędu. W gronie pozostałych graczy również nie ma trójkąta, więc istnieje gracz
; ustawmy go na początku rzędu. W gronie pozostałych graczy również nie ma trójkąta, więc istnieje gracz 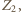 który pokonał ich wszystkich (ale nie
który pokonał ich wszystkich (ale nie 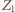 ) - ustawmy go na drugim miejscu rzędu. Kolejnych graczy ustawiamy analogicznie.
) - ustawmy go na drugim miejscu rzędu. Kolejnych graczy ustawiamy analogicznie. będzie cyklem, gdzie
będzie cyklem, gdzie 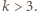 Rozważmy mecz
Rozważmy mecz 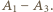 Jeśli wygrał go gracz
Jeśli wygrał go gracz 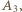 otrzymujemy trójkąt
otrzymujemy trójkąt 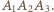 W przeciwnym przypadku otrzymujemy cykl
W przeciwnym przypadku otrzymujemy cykl 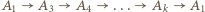 o
o 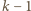 graczach. Jeśli jest ich więcej niż 3, postępujemy dalej analogicznie.
graczach. Jeśli jest ich więcej niż 3, postępujemy dalej analogicznie.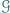 i
i 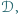 że każdy z grupy
że każdy z grupy 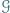 wygrał z każdym z grupy
wygrał z każdym z grupy 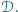
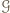 składa się tylko z niego, a grupa
składa się tylko z niego, a grupa 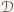 z pozostałych zawodników.
z pozostałych zawodników.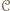 o maksymalnej długości. Jeżeli
o maksymalnej długości. Jeżeli 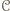 zawiera wszystkich graczy, to teza jest spełniona. W przeciwnym przypadku istnieje osoba
zawiera wszystkich graczy, to teza jest spełniona. W przeciwnym przypadku istnieje osoba 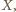 która nie należy do cyklu
która nie należy do cyklu 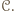 eśli istnieją cykle, to rozważmy cykl
eśli istnieją cykle, to rozważmy cykl 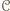 o maksymalnej długości. Jeżeli
o maksymalnej długości. Jeżeli 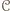 zawiera wszystkich graczy, to teza jest spełniona. W przeciwnym przypadku istnieje osoba
zawiera wszystkich graczy, to teza jest spełniona. W przeciwnym przypadku istnieje osoba 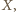 która nie należy do cyklu
która nie należy do cyklu 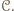
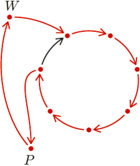
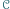
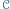
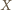 albo wygrał ze wszystkimi zawodnikami z
albo wygrał ze wszystkimi zawodnikami z 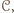 albo ze wszystkim przegrał. Załóżmy przeciwnie, że
albo ze wszystkim przegrał. Załóżmy przeciwnie, że 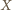 przegrał z
przegrał z 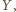 ale wygrał z
ale wygrał z 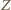 z cyklu (
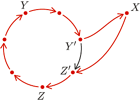
z cyklu (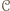 na "drodze" od
na "drodze" od 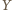 do
do 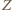 istnieją tacy dwaj kolejni zawodnicy
istnieją tacy dwaj kolejni zawodnicy 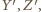 że
że 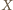 przegrał z
przegrał z 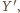 ale wygrał z
ale wygrał z 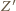 . Wtedy cykl
. Wtedy cykl 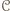 można wydłużyć, dołączając zawodnika
można wydłużyć, dołączając zawodnika 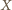 pomiędzy
pomiędzy 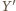 a
a 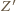 (
(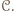
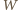 i
i 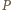 spoza cyklu
spoza cyklu 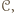 którzy odpowiednio wygrali i przegrali ze wszystkimi z cyklu, to
którzy odpowiednio wygrali i przegrali ze wszystkimi z cyklu, to 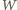 wygrał z
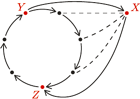
wygrał z 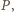 gdyż w przeciwnym razie cykl można by wydłużyć o tych dwóch graczy w sposób przedstawiony na
gdyż w przeciwnym razie cykl można by wydłużyć o tych dwóch graczy w sposób przedstawiony na 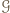 należą wszyscy zawodnicy, którzy wygrali z graczami z
należą wszyscy zawodnicy, którzy wygrali z graczami z 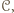 do
do 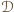 ci, którzy przegrali z uczestnikami
ci, którzy przegrali z uczestnikami 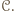 Wszystkich graczy z cyklu
Wszystkich graczy z cyklu 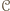 dołączmy do dowolnego spośród zbiorów
dołączmy do dowolnego spośród zbiorów  W ten sposób otrzymujemy żądany podział.
W ten sposób otrzymujemy żądany podział. został podzielony (prostymi równoległymi do boków) na
został podzielony (prostymi równoległymi do boków) na 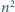 trójkącików o boku 1. Każdy wierzchołek powstałej siatki (tj. wierzchołek któregoś trójkącika) jest pomalowany na biało lub czarno. Wykonujemy ciąg ruchów. W jednym ruchu zmieniamy kolor wszystkich wierzchołków, leżących na jednej linii prostej, zawierającej bok któregoś trójkącika.
trójkącików o boku 1. Każdy wierzchołek powstałej siatki (tj. wierzchołek któregoś trójkącika) jest pomalowany na biało lub czarno. Wykonujemy ciąg ruchów. W jednym ruchu zmieniamy kolor wszystkich wierzchołków, leżących na jednej linii prostej, zawierającej bok któregoś trójkącika.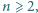 dla których - wychodząc od stanu: wszystkie wierzchołki białe - można dojść do stanu: dokładnie jeden wierzchołek czarny.
dla których - wychodząc od stanu: wszystkie wierzchołki białe - można dojść do stanu: dokładnie jeden wierzchołek czarny. wskazany cel da się osiągnąć. W trzech ruchach wybieramy proste zawierające boki dużego trójkąta. Jego wierzchołki pozostaną białe (każdy zmieni kolor dwukrotnie), zaś środki boków staną się czarne. Teraz w jednym ruchu zmieniamy kolor dwóch z tych środków z powrotem na biały. Pozostaje jeden punkt czarny.
wskazany cel da się osiągnąć. W trzech ruchach wybieramy proste zawierające boki dużego trójkąta. Jego wierzchołki pozostaną białe (każdy zmieni kolor dwukrotnie), zaś środki boków staną się czarne. Teraz w jednym ruchu zmieniamy kolor dwóch z tych środków z powrotem na biały. Pozostaje jeden punkt czarny. można uzyskać wymagany stan. Jak poprzednio, w trzech ruchach bierzemy proste, zawierające boki dużego trójkąta. Jego wierzchołki i jego środek staną się białe, pozostałe punkty siatki staną się czarne. W kolejnych trzech ruchach bierzemy proste równoległe do boków dużego trójkąta i przechodzące przez jego środek. Czarne punkty wybielą się, a punkt w środku się zaczerni.
można uzyskać wymagany stan. Jak poprzednio, w trzech ruchach bierzemy proste, zawierające boki dużego trójkąta. Jego wierzchołki i jego środek staną się białe, pozostałe punkty siatki staną się czarne. W kolejnych trzech ruchach bierzemy proste równoległe do boków dużego trójkąta i przechodzące przez jego środek. Czarne punkty wybielą się, a punkt w środku się zaczerni. nie da się! W trójce punktów, będących wierzchołkami dużego trójkąta, po każdym ruchu jest parzysta liczba czarnych punktów (0 lub 2). Żaden z tej trójki nie może więc być owym punktem, który w pewnym momencie miałby stać się jedynym czarnym.
nie da się! W trójce punktów, będących wierzchołkami dużego trójkąta, po każdym ruchu jest parzysta liczba czarnych punktów (0 lub 2). Żaden z tej trójki nie może więc być owym punktem, który w pewnym momencie miałby stać się jedynym czarnym. umieszczono 65 pionków, każdy na innym polu. Co minutę każdy pionek wykonuje ruch na pole sąsiadujące bokiem z polem, na którym się znajduje, w taki sposób, że każde kolejne dwa ruchy pionka mają prostopadłe kierunki. Wykazać, że po pewnym czasie dwa pionki znajdą się na jednym polu.
umieszczono 65 pionków, każdy na innym polu. Co minutę każdy pionek wykonuje ruch na pole sąsiadujące bokiem z polem, na którym się znajduje, w taki sposób, że każde kolejne dwa ruchy pionka mają prostopadłe kierunki. Wykazać, że po pewnym czasie dwa pionki znajdą się na jednym polu.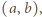 gdzie
gdzie 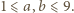 Pomalujmy pola o obu współrzędnych parzystych na niebiesko, pola o obu współrzędnych nieparzystych - na czerwono, a pozostałe pola - na żółto.
Pomalujmy pola o obu współrzędnych parzystych na niebiesko, pola o obu współrzędnych nieparzystych - na czerwono, a pozostałe pola - na żółto.