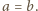Wykażemy, że jeżeli każdy element zbioru 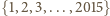 pokolorujemy na jeden z czterech kolorów w sposób losowy, to prawdopodobieństwo zdarzenia, w którym żaden rosnący
pokolorujemy na jeden z czterech kolorów w sposób losowy, to prawdopodobieństwo zdarzenia, w którym żaden rosnący 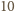 -wyrazowy ciąg arytmetyczny o wyrazach z tego zbioru nie składa się z elementów o jednakowym kolorze, jest dodatnie. Zakładamy przy tym, że każdy element malujemy na dowolny z czterech kolorów z prawdopodobieństwem
-wyrazowy ciąg arytmetyczny o wyrazach z tego zbioru nie składa się z elementów o jednakowym kolorze, jest dodatnie. Zakładamy przy tym, że każdy element malujemy na dowolny z czterech kolorów z prawdopodobieństwem 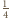 i że losowania są niezależne.
i że losowania są niezależne.
Ustalmy chwilowo pojedynczy 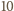 -wyrazowy ciąg arytmetyczny. Jest
-wyrazowy ciąg arytmetyczny. Jest 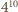 wszystkich możliwych pokolorowań tego ciągu, z których dokładnie
wszystkich możliwych pokolorowań tego ciągu, z których dokładnie 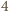 składają się wyłącznie z elementów o jednakowym kolorze. Prawdopodobieństwo tego, że ustalony ciąg składa się z elementów o jednakowym kolorze, wynosi zatem
składają się wyłącznie z elementów o jednakowym kolorze. Prawdopodobieństwo tego, że ustalony ciąg składa się z elementów o jednakowym kolorze, wynosi zatem 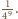 Oszacujmy od góry liczbę
Oszacujmy od góry liczbę 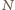 wszystkich rosnących
wszystkich rosnących 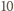 -wyrazowych ciągów arytmetycznych o wyrazach w danym zbiorze. Każdy taki ciąg jest wyznaczony przez swój wyraz początkowy
-wyrazowych ciągów arytmetycznych o wyrazach w danym zbiorze. Każdy taki ciąg jest wyznaczony przez swój wyraz początkowy 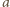 oraz różnicę
oraz różnicę 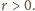 Spełnione są przy tym nierówności
Spełnione są przy tym nierówności 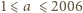 oraz
oraz 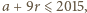 czyli
czyli 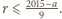 Dla ustalonego
Dla ustalonego  istnieje więc co najwyżej
istnieje więc co najwyżej 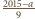 ciągów, których pierwszym wyrazem jest
ciągów, których pierwszym wyrazem jest 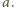 Otrzymujemy zatem nierówność
Otrzymujemy zatem nierówność
Ponumerujmy wszystkie 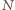 z rozważanych ciągów w sposób dowolny i dla
z rozważanych ciągów w sposób dowolny i dla 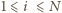 oznaczmy przez
oznaczmy przez 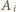 zdarzenie, w którym
zdarzenie, w którym 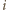 -ty ciąg zawiera elementy wyłącznie jednego koloru. Z podstawowej własności prawdopodobieństwa (tzw. subaddytywności) otrzymujemy wówczas
-ty ciąg zawiera elementy wyłącznie jednego koloru. Z podstawowej własności prawdopodobieństwa (tzw. subaddytywności) otrzymujemy wówczas
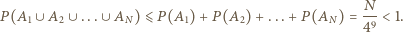
Prawdopodobieństwo zdarzenia, w którym pewien ciąg pomalowany został z użyciem wyłącznie jednego koloru, jest mniejsze niż 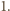 Prawdopodobieństwo dopełnienia tego zdarzenia jest więc dodatnie, co oznacza, że w pewnym kolorowaniu żaden z rozważanych ciągów nie jest jednokolorowy.
Prawdopodobieństwo dopełnienia tego zdarzenia jest więc dodatnie, co oznacza, że w pewnym kolorowaniu żaden z rozważanych ciągów nie jest jednokolorowy.
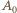 będzie tą osobą, która uczestniczyła w dokładnie dwóch występach. Przyjmijmy, że to pani; jej mąż otrzymuje oznaczenie
będzie tą osobą, która uczestniczyła w dokładnie dwóch występach. Przyjmijmy, że to pani; jej mąż otrzymuje oznaczenie 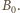 Pozostałe pary małżonków:
Pozostałe pary małżonków: 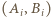 ;
; 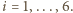 W jednym swoim występie pani
W jednym swoim występie pani 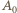 musiała się pokazać w towarzystwie połowy tych ludzi; w drugim - z pozostałą połową. Ustalmy oznaczenia tak, że w jednym z tych występów uczestniczyły osoby
musiała się pokazać w towarzystwie połowy tych ludzi; w drugim - z pozostałą połową. Ustalmy oznaczenia tak, że w jednym z tych występów uczestniczyły osoby 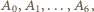 a w drugim
a w drugim 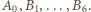 I znów, bez straty ogólności, możemy przyjąć (dla wygody języka), że osoby
I znów, bez straty ogólności, możemy przyjąć (dla wygody języka), że osoby 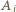 to panie, a
to panie, a 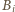 panowie (w kontekście tego zadania szybka zmiana płci to nie problem).
panowie (w kontekście tego zadania szybka zmiana płci to nie problem).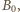 co najwyżej dwie osoby - bo gdyby więcej, to byłyby/byliby wśród nich dwie panie lub dwaj panowie; a przecież one/oni już się pokazali wspólnie, wraz z panią
co najwyżej dwie osoby - bo gdyby więcej, to byłyby/byliby wśród nich dwie panie lub dwaj panowie; a przecież one/oni już się pokazali wspólnie, wraz z panią 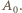
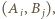 gdzie
gdzie 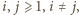 musiała raz wspólnie wystąpić; i były to różne występy. Jest 30 takich par. Uwzględniając dwa występy z udziałem pani
musiała raz wspólnie wystąpić; i były to różne występy. Jest 30 takich par. Uwzględniając dwa występy z udziałem pani 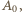 widzimy, że liczba występów musiała wynieść co najmniej 32.
widzimy, że liczba występów musiała wynieść co najmniej 32.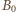 wspólne uczestnictwo z każdą osobą poza panią
wspólne uczestnictwo z każdą osobą poza panią 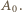 Uzyskamy to, dołączając go (na przykład) do par
Uzyskamy to, dołączając go (na przykład) do par 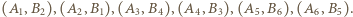 Zostaną przez to spełnione wszystkie wymagane warunki. Tak więc szukane minimum wynosi 32.
Zostaną przez to spełnione wszystkie wymagane warunki. Tak więc szukane minimum wynosi 32.
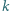 jest pewną liczbą naturalną.
jest pewną liczbą naturalną.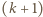 -szy. W pojedynczym rzucie prawdopodobieństwo wyrzucenia orła jest równe
-szy. W pojedynczym rzucie prawdopodobieństwo wyrzucenia orła jest równe 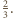 Z prawdopodobieństwem
Z prawdopodobieństwem 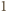 takie doświadczenie zakończy się po skończonej liczbie rzutów. Z drugiej strony prawdopodobieństwo zakończenia doświadczenia po dokładnie
takie doświadczenie zakończy się po skończonej liczbie rzutów. Z drugiej strony prawdopodobieństwo zakończenia doświadczenia po dokładnie 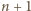 rzutach wynosi
rzutach wynosi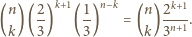
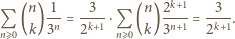

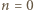 suma
suma 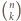 równa jest
równa jest 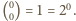 W kolejnych wierszach, na mocy
W kolejnych wierszach, na mocy 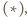 suma liczb jest dwukrotnością sumy poprzedniego wiersza, uzyskujemy więc kolejne potęgi dwójki.
suma liczb jest dwukrotnością sumy poprzedniego wiersza, uzyskujemy więc kolejne potęgi dwójki.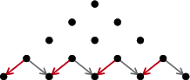
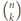 dla
dla 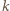 parzystych równa jest sumie
parzystych równa jest sumie 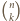 dla
dla 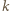 nieparzystych (i równa sumie wyrazów poprzedniego wiersza). Stąd różnica tych dwóch sum daje zero.
nieparzystych (i równa sumie wyrazów poprzedniego wiersza). Stąd różnica tych dwóch sum daje zero.
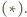

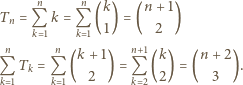
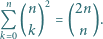

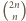 jest środkowym wyrazem wiersza numer
jest środkowym wyrazem wiersza numer 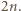 Na mocy
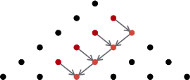
Na mocy 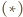 jest on sumą dwóch wyrazów nad nim, a więc też sumą trzech wyrazów o dwa wiersze wyżej, przy czym środkowy z nich liczymy dwukrotnie. Stąd jest także sumą czterech środkowych wyrazów jeszcze wyższego wiersza, liczonych z krotnościami odpowiednio 1, 3, 3, 1, itd. Na rysunku 5 zilustrowano uzyskane w ten sposób dwa "przenikające się" trójkąty Pascala - wyjściowy oraz drugi "do góry nogami", oznaczający krotności, z jakimi liczyć należy wyrazy z coraz wyższych wierszy.
jest on sumą dwóch wyrazów nad nim, a więc też sumą trzech wyrazów o dwa wiersze wyżej, przy czym środkowy z nich liczymy dwukrotnie. Stąd jest także sumą czterech środkowych wyrazów jeszcze wyższego wiersza, liczonych z krotnościami odpowiednio 1, 3, 3, 1, itd. Na rysunku 5 zilustrowano uzyskane w ten sposób dwa "przenikające się" trójkąty Pascala - wyjściowy oraz drugi "do góry nogami", oznaczający krotności, z jakimi liczyć należy wyrazy z coraz wyższych wierszy. -ty wiersz i stąd
-ty wiersz i stąd 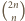 jest sumą wyrazów tego wiersza, liczonych z krotnościami odpowiadającymi im samym, co kończy dowód.
jest sumą wyrazów tego wiersza, liczonych z krotnościami odpowiadającymi im samym, co kończy dowód.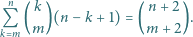
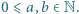 Wyznacz sumę tych
Wyznacz sumę tych 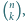 dla których
dla których 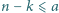 oraz
oraz 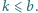

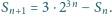
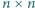 wpisano w pewnej kolejności liczby
wpisano w pewnej kolejności liczby 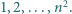 Powiemy, że para liczb sąsiaduje, jeśli znajdują się one obok siebie w pewnym wierszu lub w pewnej kolumnie. Wykazać, że istnieje para sąsiadujących liczb, które różnią się co najmniej o
Powiemy, że para liczb sąsiaduje, jeśli znajdują się one obok siebie w pewnym wierszu lub w pewnej kolumnie. Wykazać, że istnieje para sąsiadujących liczb, które różnią się co najmniej o 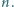
 będzie najmniejszą liczbą, dla której istnieje linia złożona z liczb nie większych od
będzie najmniejszą liczbą, dla której istnieje linia złożona z liczb nie większych od  Możemy zakładać, że tą linią jest pierwszy wiersz, a jego pierwszym wyrazem jest
Możemy zakładać, że tą linią jest pierwszy wiersz, a jego pierwszym wyrazem jest 
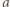 i
i 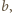 że
że 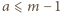 i
i 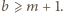 Dla ustalenia uwagi weźmy drugą kolumnę. Jej pierwszy wyraz nie może być większy od
Dla ustalenia uwagi weźmy drugą kolumnę. Jej pierwszy wyraz nie może być większy od 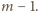 Niech
Niech 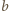 będzie najwyżej położonym wyrazem drugiej kolumny, który jest większy od
będzie najwyżej położonym wyrazem drugiej kolumny, który jest większy od  (musi taki istnieć wobec definicji
(musi taki istnieć wobec definicji  ). Wyraz położony nad
). Wyraz położony nad 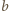 jest szukanym
jest szukanym 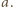
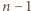 par liczb
par liczb 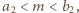
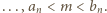 Największa spośród liczb
Największa spośród liczb 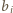 musi więc wynosić co najmniej
musi więc wynosić co najmniej 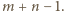 W takim razie
W takim razie 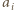 oraz
oraz 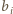 są poszukiwanymi liczbami.
są poszukiwanymi liczbami.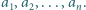 Ruch polega na wyborze dwóch takich indeksów
Ruch polega na wyborze dwóch takich indeksów 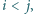 że
że 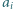 nie dzieli
nie dzieli 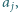 i zastąpieniu liczb
i zastąpieniu liczb 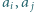 przez odpowiednio ich największy wspólny dzielnik i najmniejszą wspólną wielokrotność. Udowodnić, że nie jest możliwe wykonanie nieskończenie wielu ruchów.
przez odpowiednio ich największy wspólny dzielnik i najmniejszą wspólną wielokrotność. Udowodnić, że nie jest możliwe wykonanie nieskończenie wielu ruchów.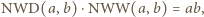 to iloczyn
to iloczyn 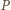 wszystkich wyrazów ciągu nie zmienia się po wykonaniu ruchu. W szczególności każdy z wyrazów ciągu jest ograniczony z góry przez
wszystkich wyrazów ciągu nie zmienia się po wykonaniu ruchu. W szczególności każdy z wyrazów ciągu jest ograniczony z góry przez 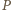 i ograniczony z dołu przez
i ograniczony z dołu przez 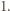 Ponadto w każdym ruchu, modyfikującym pewne wyrazy o indeksach
Ponadto w każdym ruchu, modyfikującym pewne wyrazy o indeksach 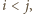 liczba
liczba 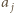 jest zamieniana na większą
jest zamieniana na większą 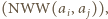 liczba
liczba 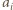 zaś - na mniejszą
zaś - na mniejszą 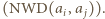 Żaden wyraz ciągu nie może być nieskończenie wiele razy zmniejszany (jako ograniczony z dołu przez
Żaden wyraz ciągu nie może być nieskończenie wiele razy zmniejszany (jako ograniczony z dołu przez 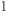 ) ani zwiększany (jako ograniczony z góry przez
) ani zwiększany (jako ograniczony z góry przez 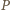 ). W takim razie każdy wyraz zostanie zmieniony skończenie wiele razy, czyli nie możemy wykonać nieskończenie wielu ruchów.
). W takim razie każdy wyraz zostanie zmieniony skończenie wiele razy, czyli nie możemy wykonać nieskończenie wielu ruchów. ) i zastąpieniu jej liczbą
) i zastąpieniu jej liczbą 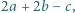 gdzie
gdzie 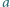 i
i 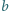 to dwie pozostałe liczby. Rozstrzygnąć, czy za pomocą takich ruchów możemy uzyskać na tablicy trójkę liczb 20, 21, 24? A trójkę 20, 21, 23?
to dwie pozostałe liczby. Rozstrzygnąć, czy za pomocą takich ruchów możemy uzyskać na tablicy trójkę liczb 20, 21, 24? A trójkę 20, 21, 23?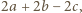 czyli o liczbę parzystą. Stąd parzystość sumy liczb napisanych na tablicy nie zmienia się, więc nie możemy uzyskać trójki 20, 21, 24.
czyli o liczbę parzystą. Stąd parzystość sumy liczb napisanych na tablicy nie zmienia się, więc nie możemy uzyskać trójki 20, 21, 24. nie zmienia się przy zamianie
nie zmienia się przy zamianie  na
na 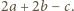 Ponieważ dla trójki 11, 12, 13 ta wartość wynosi -428, a dla trójki 20, 21, 23 wynosi ona -1356, to również tej trójki nie możemy uzyskać na tablicy.
Ponieważ dla trójki 11, 12, 13 ta wartość wynosi -428, a dla trójki 20, 21, 23 wynosi ona -1356, to również tej trójki nie możemy uzyskać na tablicy.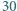 połączeń telefonicznych (każde pomiędzy jednym z 10 chłopców i jedną z 10 dziewczyn) w taki sposób, aby żadna para osób nie rozmawiała ze sobą dwukrotnie oraz aby w każdej czwórce złożonej z dwóch chłopców i dwóch dziewczyn istniały dwie osoby różnej płci, które ze sobą nie rozmawiały.
połączeń telefonicznych (każde pomiędzy jednym z 10 chłopców i jedną z 10 dziewczyn) w taki sposób, aby żadna para osób nie rozmawiała ze sobą dwukrotnie oraz aby w każdej czwórce złożonej z dwóch chłopców i dwóch dziewczyn istniały dwie osoby różnej płci, które ze sobą nie rozmawiały.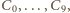 a dziewczyny -
a dziewczyny - 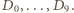 Niech dla każdego
Niech dla każdego 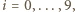 chłopiec
chłopiec 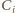 zadzwoni do
zadzwoni do 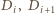 oraz
oraz 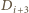 (gdzie
(gdzie 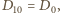
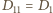 i
i 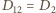 ). Wówczas zostanie wykonanych łącznie
). Wówczas zostanie wykonanych łącznie 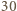 połączeń i pierwszy warunek będzie spełniony w sposób oczywisty. Aby sprawdzić drugi warunek, spójrzmy na tabelę połączeń ("1" oznacza, że
połączeń i pierwszy warunek będzie spełniony w sposób oczywisty. Aby sprawdzić drugi warunek, spójrzmy na tabelę połączeń ("1" oznacza, że 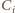 zadzwoni do
zadzwoni do 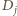 ).
).
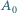 będzie ustalonym wierzchołkiem
będzie ustalonym wierzchołkiem 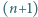 -kąta foremnego. Numerujemy pozostałe wierzchołki
-kąta foremnego. Numerujemy pozostałe wierzchołki 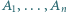 w dowolnej kolejności. Każdemu bokowi
w dowolnej kolejności. Każdemu bokowi 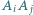 przyporządkowujemy liczbę
przyporządkowujemy liczbę 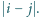 Niech
Niech 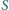 będzie sumą
będzie sumą 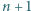 liczb, przyporządkowanych wszystkim bokom. Dla zadanej liczby naturalnej
liczb, przyporządkowanych wszystkim bokom. Dla zadanej liczby naturalnej  :
: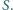
 wierzchołków (poza
wierzchołków (poza 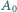 ), przy których
), przy których 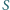 osiąga ową minimalną wartość.
osiąga ową minimalną wartość.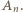 Idąc od
Idąc od 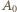 do
do 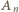 wzdłuż brzegu wielokąta, w wybranym kierunku, mijamy kolejno wierzchołki
wzdłuż brzegu wielokąta, w wybranym kierunku, mijamy kolejno wierzchołki 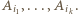 Przechodzimy przez
Przechodzimy przez 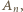 dalej mijamy wierzchołki
dalej mijamy wierzchołki 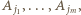 i wracamy do
i wracamy do 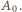 Numery
Numery 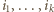 oraz
oraz 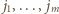 tworzą permutację zbioru
tworzą permutację zbioru 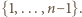 Liczby, przyporządkowane wszystkim bokom, sumują się do wartości
Liczby, przyporządkowane wszystkim bokom, sumują się do wartości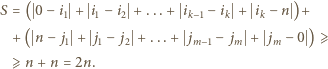
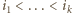 oraz
oraz 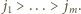 Zatem
Zatem 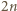 to szukane minimum.
to szukane minimum.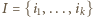 może być dowolnym podzbiorem zbioru
może być dowolnym podzbiorem zbioru 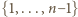 (również pustym, wtedy pierwszy składnik rozpisanej sumy
(również pustym, wtedy pierwszy składnik rozpisanej sumy 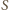 ma postać
ma postać 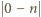 ). Zauważmy teraz, że już sam wybór zbioru
). Zauważmy teraz, że już sam wybór zbioru 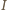 determinuje ponumerowanie, realizujące równość
determinuje ponumerowanie, realizujące równość 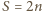 ; liczby ze zbioru
; liczby ze zbioru 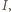 uporządkowane rosnąco, trzeba przypisać kolejnym wierzchołkom (przy obieganiu wielokąta od
uporządkowane rosnąco, trzeba przypisać kolejnym wierzchołkom (przy obieganiu wielokąta od 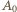 w wybranym kierunku), następny wierzchołek trzeba nazwać
w wybranym kierunku), następny wierzchołek trzeba nazwać 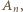 a dalszym wierzchołkom dać niewykorzystane numery, uporządkowane malejąco.
a dalszym wierzchołkom dać niewykorzystane numery, uporządkowane malejąco.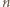 wierzchołków, ile podzbiorów ma zbiór
wierzchołków, ile podzbiorów ma zbiór 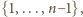 to znaczy
to znaczy 
 osób zna dokładnie jedną wiadomość i każda z tych
osób zna dokładnie jedną wiadomość i każda z tych 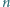 wiadomości jest inna. Co jakiś czas pewna osoba dzwoni do innej i przekazuje jej wszystko, co wie (nie poznając żadnej informacji w zamian). Ile co najmniej rozmów telefonicznych musi się odbyć, zanim wszystkie osoby będą znać wszystkie informacje?
wiadomości jest inna. Co jakiś czas pewna osoba dzwoni do innej i przekazuje jej wszystko, co wie (nie poznając żadnej informacji w zamian). Ile co najmniej rozmów telefonicznych musi się odbyć, zanim wszystkie osoby będą znać wszystkie informacje?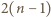 połączeń wystarczy. Ustalmy pewną osobę
połączeń wystarczy. Ustalmy pewną osobę 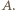 Najpierw każda z pozostałych osób dzwoni do
Najpierw każda z pozostałych osób dzwoni do 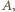 przekazując jej swoją informację. Wówczas osoba
przekazując jej swoją informację. Wówczas osoba 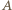 zna już wszystkie informacje i w ciągu kolejnych
zna już wszystkie informacje i w ciągu kolejnych 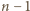 rozmów może przekazać je pozostałym.
rozmów może przekazać je pozostałym.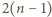 połączeń. Niech
połączeń. Niech  oznacza liczbę wszystkich wykonanych w tym celu połączeń,
oznacza liczbę wszystkich wykonanych w tym celu połączeń, 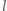 zaś - liczbę połączeń, które zostały wykonane przed pierwszym momentem, gdy pewna osoba (nazwijmy ją
zaś - liczbę połączeń, które zostały wykonane przed pierwszym momentem, gdy pewna osoba (nazwijmy ją 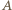 ) znała wszystkie
) znała wszystkie  wiadomości. Każda z pozostałych
wiadomości. Każda z pozostałych 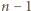 osób musi być poinformowana o wiadomościach, których nie zna, więc trzeba wykonać jeszcze co najmniej
osób musi być poinformowana o wiadomościach, których nie zna, więc trzeba wykonać jeszcze co najmniej 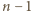 połączeń, tzn.
połączeń, tzn. 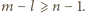 Zauważmy również, że po
Zauważmy również, że po 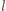 telefonach osoba
telefonach osoba 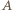 zna wszystkie wiadomości, więc każda z
zna wszystkie wiadomości, więc każda z 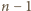 pozostałych osób musiała wykonać wcześniej przynajmniej jedno połączenie (inaczej jej wiadomość nie byłaby znana nikomu poza nią, w szczególności
pozostałych osób musiała wykonać wcześniej przynajmniej jedno połączenie (inaczej jej wiadomość nie byłaby znana nikomu poza nią, w szczególności 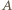 ). Stąd
). Stąd 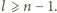 W takim razie
W takim razie 
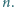 W turnieju, w którym bierze udział
W turnieju, w którym bierze udział 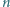 drużyn, zostanie rozegranych
drużyn, zostanie rozegranych 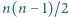 meczów każdy z każdym. Wykazać, że możliwe jest takie podzielenie rozgrywek na
meczów każdy z każdym. Wykazać, że możliwe jest takie podzielenie rozgrywek na  rund, by każda drużyna wystąpiła w każdej rundzie dokładnie raz.
rund, by każda drużyna wystąpiła w każdej rundzie dokładnie raz.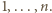 Niech w
Niech w 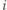 -tej rundzie (dla
-tej rundzie (dla 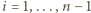 ) drużyny
) drużyny 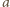 i
i 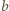 (dla
(dla 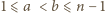 ) grają ze sobą, jeśli
) grają ze sobą, jeśli 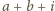 jest podzielne przez
jest podzielne przez 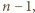 zaś drużyny
zaś drużyny 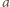 i
i 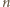 (dla
(dla 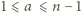 ) - jeśli
) - jeśli 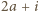 jest podzielne przez
jest podzielne przez 
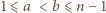 dokładnie jedna spośród
dokładnie jedna spośród 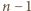 kolejnych liczb
kolejnych liczb 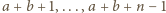 jest podzielna przez
jest podzielna przez 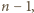 więc
więc  i
i 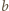 zagrają ze sobą w dokładnie jednej z rund. Podobnie drużyny
zagrają ze sobą w dokładnie jednej z rund. Podobnie drużyny 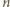 i
i 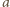 dla
dla 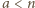 zagrają ze sobą dokładnie raz, ponieważ dokładnie jedna z liczb
zagrają ze sobą dokładnie raz, ponieważ dokładnie jedna z liczb 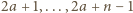 jest podzielna przez
jest podzielna przez 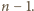
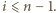 Gdyby drużyna
Gdyby drużyna  grała w
grała w 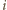 -tej rundzie dwa razy, to dla pewnych
-tej rundzie dwa razy, to dla pewnych  liczba
liczba 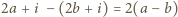 byłaby podzielna przez
byłaby podzielna przez  Ponieważ
Ponieważ  jest parzyste, dostalibyśmy, że
jest parzyste, dostalibyśmy, że  co jest niemożliwe. Gdyby drużyna
co jest niemożliwe. Gdyby drużyna  grała dwa razy w
grała dwa razy w 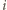 -tej rundzie, to zachodziłaby jedna z dwóch możliwości: 1) drużyna
-tej rundzie, to zachodziłaby jedna z dwóch możliwości: 1) drużyna  gra z drużynami
gra z drużynami 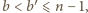 skąd
skąd 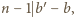 a to jest niemożliwe; 2) drużyna
a to jest niemożliwe; 2) drużyna  gra z drużynami
gra z drużynami  i
i  skąd
skąd 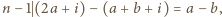 co również jest niemożliwe.
co również jest niemożliwe.
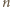 swoich ruchach Maja maluje na kolorowo
swoich ruchach Maja maluje na kolorowo 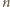 punktów z jednej prostej. Każdą parę takich kolorowych punktów można na dwa sposoby uzupełnić do trójkąta równobocznego, par punktów spośród
punktów z jednej prostej. Każdą parę takich kolorowych punktów można na dwa sposoby uzupełnić do trójkąta równobocznego, par punktów spośród  jest
jest 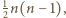 więc łącznie po
więc łącznie po 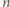 ruchach na płaszczyźnie jest
ruchach na płaszczyźnie jest 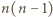 takich punktów, że pomalowanie dowolnego z nich na kolorowo da Mai zwycięstwo.
takich punktów, że pomalowanie dowolnego z nich na kolorowo da Mai zwycięstwo.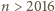 mamy
mamy 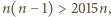 zatem Gucio nie może w swoich początkowych
zatem Gucio nie może w swoich początkowych 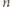 ruchach wszystkich opisanych powyżej punktów pomalować na czarno i Maja może wygrać w ruchu numer
ruchach wszystkich opisanych powyżej punktów pomalować na czarno i Maja może wygrać w ruchu numer 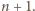
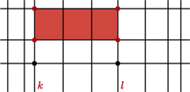
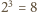 możliwych układów kolorów trójki wyróżnionych punktów z pojedynczej pionowej prostej. Ponieważ mamy 9 pionowych prostych, na pewnych dwóch z nich (nazwijmy je
możliwych układów kolorów trójki wyróżnionych punktów z pojedynczej pionowej prostej. Ponieważ mamy 9 pionowych prostych, na pewnych dwóch z nich (nazwijmy je 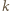 i
i 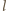 ) jest ten sam układ kolorów takiej trójki.
) jest ten sam układ kolorów takiej trójki.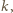 pomalowanych dwoma kolorami, pewne dwa punkty mają ten sam kolor. Niech to będą dwa wierzchołki szukanego prostokąta, pozostałe dwa to odpowiadające im punkty tego samego koloru z prostej
pomalowanych dwoma kolorami, pewne dwa punkty mają ten sam kolor. Niech to będą dwa wierzchołki szukanego prostokąta, pozostałe dwa to odpowiadające im punkty tego samego koloru z prostej 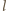 (leżą one na tych samych poziomych prostych).
(leżą one na tych samych poziomych prostych).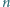 kolorów
kolorów 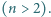 Wykaż, że istnieje na tej płaszczyźnie prostokąt o wierzchołkach jednego koloru.
Wykaż, że istnieje na tej płaszczyźnie prostokąt o wierzchołkach jednego koloru.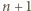 prostych poziomych oraz
prostych poziomych oraz 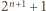 prostych pionowych.
prostych pionowych.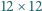 pomalowano jednym z trzech kolorów. Wykaż, że istnieją cztery pola o tym samym kolorze, których środki są wierzchołkami prostokąta.
pomalowano jednym z trzech kolorów. Wykaż, że istnieją cztery pola o tym samym kolorze, których środki są wierzchołkami prostokąta.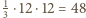 pól. Rozważmy 48 pól tego właśnie koloru i niech
pól. Rozważmy 48 pól tego właśnie koloru i niech 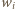 oznacza liczbę tych pól występujących w
oznacza liczbę tych pól występujących w 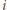 -tym wierszu; oczywiście
-tym wierszu; oczywiście 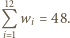 W każdym wierszu dwa spośród rozważanych pól można wybrać na
W każdym wierszu dwa spośród rozważanych pól można wybrać na 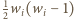 sposobów. Wobec tego
sposobów. Wobec tego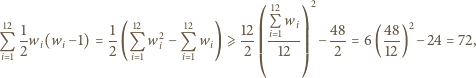
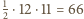 sposobów - mniej niż 72. Oznacza to, że w pewnych dwóch wierszach można wybrać po dwa pola tego samego koloru i w tych samych kolumnach; ich środki tworzą szukany prostokąt.
sposobów - mniej niż 72. Oznacza to, że w pewnych dwóch wierszach można wybrać po dwa pola tego samego koloru i w tych samych kolumnach; ich środki tworzą szukany prostokąt.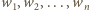 zachodzi nierówność między średnią kwadratową a arytmetyczną:
zachodzi nierówność między średnią kwadratową a arytmetyczną: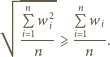
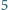 rycerzy, w której nie będzie wrogów?
rycerzy, w której nie będzie wrogów?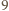 osób musimy wybrać
osób musimy wybrać 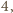 które nie siedzą na sąsiadujących miejscach. Możemy to zrobić na
które nie siedzą na sąsiadujących miejscach. Możemy to zrobić na 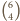 sposobów, ponieważ wybrane osoby jednoznacznie odpowiadają miejscom, a więc wstawieniu pomiędzy
sposobów, ponieważ wybrane osoby jednoznacznie odpowiadają miejscom, a więc wstawieniu pomiędzy 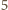 miejsc osób spoza drużyny (lub przed pierwszym z nich, lub za ostatnim)
miejsc osób spoza drużyny (lub przed pierwszym z nich, lub za ostatnim) 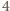 miejsc dla osób z drużyny.
miejsc dla osób z drużyny.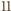 osób musimy wybrać
osób musimy wybrać 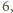 niebędących wrogami. W tym przypadku drużynę można wybrać na
niebędących wrogami. W tym przypadku drużynę można wybrać na 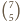 sposobów: pomiędzy
sposobów: pomiędzy 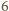 miejsc dla osób spoza drużyny (lub przed pierwszym z nich, lub za ostatnim) wstawiamy
miejsc dla osób spoza drużyny (lub przed pierwszym z nich, lub za ostatnim) wstawiamy 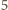 miejsc dla osób z drużyny.
miejsc dla osób z drużyny.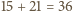 sposobów.
sposobów.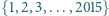 na jeden z czterech kolorów w taki sposób, że żaden rosnący 10-wyrazowy ciąg arytmetyczny o wyrazach z tego zbioru nie składa się z elementów o jednakowym kolorze.
na jeden z czterech kolorów w taki sposób, że żaden rosnący 10-wyrazowy ciąg arytmetyczny o wyrazach z tego zbioru nie składa się z elementów o jednakowym kolorze.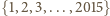 pokolorujemy na jeden z czterech kolorów w sposób losowy, to prawdopodobieństwo zdarzenia, w którym żaden rosnący
pokolorujemy na jeden z czterech kolorów w sposób losowy, to prawdopodobieństwo zdarzenia, w którym żaden rosnący 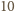 -wyrazowy ciąg arytmetyczny o wyrazach z tego zbioru nie składa się z elementów o jednakowym kolorze, jest dodatnie. Zakładamy przy tym, że każdy element malujemy na dowolny z czterech kolorów z prawdopodobieństwem
-wyrazowy ciąg arytmetyczny o wyrazach z tego zbioru nie składa się z elementów o jednakowym kolorze, jest dodatnie. Zakładamy przy tym, że każdy element malujemy na dowolny z czterech kolorów z prawdopodobieństwem 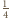 i że losowania są niezależne.
i że losowania są niezależne.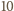 -wyrazowy ciąg arytmetyczny. Jest
-wyrazowy ciąg arytmetyczny. Jest 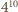 wszystkich możliwych pokolorowań tego ciągu, z których dokładnie
wszystkich możliwych pokolorowań tego ciągu, z których dokładnie 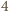 składają się wyłącznie z elementów o jednakowym kolorze. Prawdopodobieństwo tego, że ustalony ciąg składa się z elementów o jednakowym kolorze, wynosi zatem
składają się wyłącznie z elementów o jednakowym kolorze. Prawdopodobieństwo tego, że ustalony ciąg składa się z elementów o jednakowym kolorze, wynosi zatem 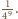 Oszacujmy od góry liczbę
Oszacujmy od góry liczbę 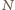 wszystkich rosnących
wszystkich rosnących 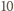 -wyrazowych ciągów arytmetycznych o wyrazach w danym zbiorze. Każdy taki ciąg jest wyznaczony przez swój wyraz początkowy
-wyrazowych ciągów arytmetycznych o wyrazach w danym zbiorze. Każdy taki ciąg jest wyznaczony przez swój wyraz początkowy 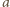 oraz różnicę
oraz różnicę 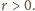 Spełnione są przy tym nierówności
Spełnione są przy tym nierówności 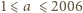 oraz
oraz 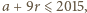 czyli
czyli 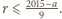 Dla ustalonego
Dla ustalonego  istnieje więc co najwyżej
istnieje więc co najwyżej 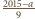 ciągów, których pierwszym wyrazem jest
ciągów, których pierwszym wyrazem jest 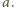 Otrzymujemy zatem nierówność
Otrzymujemy zatem nierówność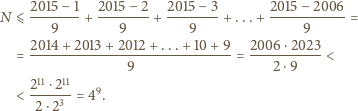
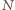 z rozważanych ciągów w sposób dowolny i dla
z rozważanych ciągów w sposób dowolny i dla 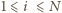 oznaczmy przez
oznaczmy przez 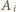 zdarzenie, w którym
zdarzenie, w którym 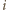 -ty ciąg zawiera elementy wyłącznie jednego koloru. Z podstawowej własności prawdopodobieństwa (tzw. subaddytywności) otrzymujemy wówczas
-ty ciąg zawiera elementy wyłącznie jednego koloru. Z podstawowej własności prawdopodobieństwa (tzw. subaddytywności) otrzymujemy wówczas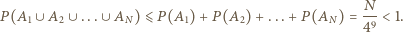
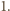 Prawdopodobieństwo dopełnienia tego zdarzenia jest więc dodatnie, co oznacza, że w pewnym kolorowaniu żaden z rozważanych ciągów nie jest jednokolorowy.
Prawdopodobieństwo dopełnienia tego zdarzenia jest więc dodatnie, co oznacza, że w pewnym kolorowaniu żaden z rozważanych ciągów nie jest jednokolorowy.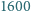 -osobowym stowarzyszeniu działa
-osobowym stowarzyszeniu działa 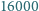 komisji, z których każda złożona jest z
komisji, z których każda złożona jest z 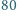 osób. Udowodnić, że pewne dwie różne komisje mają przynajmniej czterech wspólnych członków.
osób. Udowodnić, że pewne dwie różne komisje mają przynajmniej czterech wspólnych członków.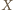 liczbę wspólnych członków tej pary. Niech
liczbę wspólnych członków tej pary. Niech 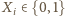 będzie funkcją charakterystyczną
będzie funkcją charakterystyczną 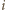 -tej osoby, czyli
-tej osoby, czyli 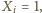 jeżeli
jeżeli 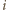 -ta osoba należy do obu wylosowanych komisji oraz
-ta osoba należy do obu wylosowanych komisji oraz 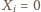 w przeciwnym przypadku. Funkcje
w przeciwnym przypadku. Funkcje 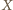 oraz
oraz 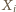 są zmiennymi losowymi. Ponieważ
są zmiennymi losowymi. Ponieważ 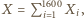 więc zachodzi równość
więc zachodzi równość ![|E[X]](/math/temat/matematyka/kombinatoryka/zadania/2015/03/29/zm-15_04-metody-3/10x-081b9846768cfbd773023286d0e3f4b920dfc8c7-im-66,57,43-FF,FF,FF.gif) Jednocześnie wprost z definicji wartości oczekiwanej wynika, że liczba
Jednocześnie wprost z definicji wartości oczekiwanej wynika, że liczba ![| E[Xi]](/math/temat/matematyka/kombinatoryka/zadania/2015/03/29/zm-15_04-metody-3/11x-081b9846768cfbd773023286d0e3f4b920dfc8c7-im-66,57,43-FF,FF,FF.gif) jest w rzeczywistości prawdopodobieństwem tego, że
jest w rzeczywistości prawdopodobieństwem tego, że 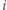 -ta osoba należy do obu z wylosowanych komisji. Jeśli przez
-ta osoba należy do obu z wylosowanych komisji. Jeśli przez 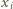 oznaczymy więc liczbę komisji, do których należy
oznaczymy więc liczbę komisji, do których należy 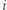 -ta osoba ze stowarzyszenia, to zachodzi równość
-ta osoba ze stowarzyszenia, to zachodzi równość![E[Xi]](/math/temat/matematyka/kombinatoryka/zadania/2015/03/29/zm-15_04-metody-3/15x-081b9846768cfbd773023286d0e3f4b920dfc8c7-dm-66,57,43-FF,FF,FF.gif)
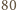 członków, to mamy ponadto
członków, to mamy ponadto 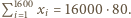 Wykorzystując nierówność między średnią arytmetyczną a kwadratową, otrzymujemy
Wykorzystując nierówność między średnią arytmetyczną a kwadratową, otrzymujemy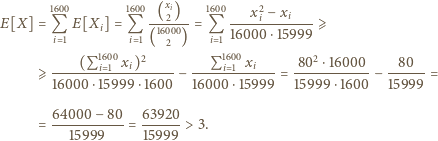
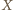 przyjmuje wyłącznie wartości całkowite, a więc skoro jej wartość oczekiwana jest większa niż
przyjmuje wyłącznie wartości całkowite, a więc skoro jej wartość oczekiwana jest większa niż 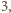 to co najmniej raz przyjmuje ona wartość nie mniejszą niż
to co najmniej raz przyjmuje ona wartość nie mniejszą niż 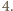 Istnieje więc para różnych komisji, która ma przynajmniej czterech wspólnych członków.
Istnieje więc para różnych komisji, która ma przynajmniej czterech wspólnych członków.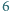 zadań. Każde z zadań zostało rozwiązane przez przynajmniej
zadań. Każde z zadań zostało rozwiązane przez przynajmniej 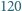 uczniów. Udowodnić, że istnieją tacy dwaj uczniowie, że każde z zadań zostało rozwiązane przez przynajmniej jednego z nich.
uczniów. Udowodnić, że istnieją tacy dwaj uczniowie, że każde z zadań zostało rozwiązane przez przynajmniej jednego z nich.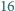 znajduje się
znajduje się 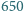 punktów. Mamy do dyspozycji pierścień, który powstał przez usunięcie koła o promieniu
punktów. Mamy do dyspozycji pierścień, który powstał przez usunięcie koła o promieniu 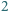 ze współśrodkowego z nim koła o promieniu
ze współśrodkowego z nim koła o promieniu 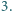 Wykazać, że ów pierścień można umieścić na płaszczyźnie w taki sposób, że przykrywa on przynajmniej
Wykazać, że ów pierścień można umieścić na płaszczyźnie w taki sposób, że przykrywa on przynajmniej 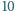 z danych punktów.
z danych punktów.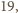 które jest współśrodkowe z danym. Udowodnij, że jeżeli środek pierścienia umieścimy w tym punkcie, to wartość oczekiwana liczby przykrytych punktów jest większa niż
które jest współśrodkowe z danym. Udowodnij, że jeżeli środek pierścienia umieścimy w tym punkcie, to wartość oczekiwana liczby przykrytych punktów jest większa niż 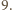
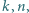 że
że 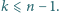 Zbiory
Zbiory 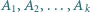 są niepustymi podzbiorami zbioru
są niepustymi podzbiorami zbioru 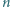 -elementowego
-elementowego 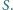 Udowodnić, że można pokolorować pewne elementy zbioru
Udowodnić, że można pokolorować pewne elementy zbioru 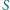 dwoma kolorami w taki sposób, że spełnione są następujące warunki:
dwoma kolorami w taki sposób, że spełnione są następujące warunki: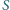 jest albo niepokolorowany, albo pokolorowany na jeden z dwóch kolorów.
jest albo niepokolorowany, albo pokolorowany na jeden z dwóch kolorów.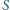 jest pokolorowany.
jest pokolorowany.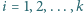 zbiór
zbiór 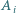 jest albo całkowicie niepokolorowany, albo zawiera elementy obu kolorów.
jest albo całkowicie niepokolorowany, albo zawiera elementy obu kolorów.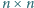 wpisano po kolei liczby
wpisano po kolei liczby  Następnie wybrano z niej
Następnie wybrano z niej 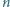 liczb tak, że w każdym wierszu i w każdej kolumnie znajduje się dokładnie jedna z wybranych liczb. Wyznaczyć wszystkie możliwe wartości sumy wybranych liczb.
liczb tak, że w każdym wierszu i w każdej kolumnie znajduje się dokładnie jedna z wybranych liczb. Wyznaczyć wszystkie możliwe wartości sumy wybranych liczb.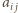 oznacza liczbę w
oznacza liczbę w 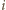 -tym wierszu i
-tym wierszu i 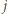 -tej kolumnie naszej tablicy,
-tej kolumnie naszej tablicy,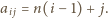
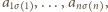 gdzie
gdzie 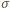 to pewna permutacja zbioru
to pewna permutacja zbioru 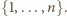 Suma wybranych liczb wynosi w takim razie
Suma wybranych liczb wynosi w takim razie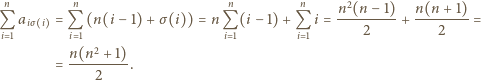
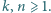 Na tablicy napisano w pewnej kolejności wszystkie dodatnie liczby całkowite nieprzekraczające
Na tablicy napisano w pewnej kolejności wszystkie dodatnie liczby całkowite nieprzekraczające 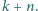 Ruch polega na zamianie miejscami dwóch liczb różniących się o
Ruch polega na zamianie miejscami dwóch liczb różniących się o 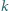 albo o
albo o 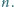 Dowieść, że można wykonać ciąg ruchów, który doprowadzi liczby na tablicy do kolejności
Dowieść, że można wykonać ciąg ruchów, który doprowadzi liczby na tablicy do kolejności 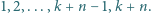
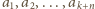 oznacza dany ciąg. Niech
oznacza dany ciąg. Niech 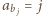 dla
dla 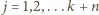 - ta równość definiuje jednoznacznie liczbę
- ta równość definiuje jednoznacznie liczbę 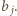 Dla ciągu
Dla ciągu 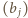 ruch polega na zamianie jego dwóch wyrazów znajdujących się w odległości
ruch polega na zamianie jego dwóch wyrazów znajdujących się w odległości 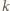 lub
lub 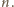 Jeśli umiemy posortować drugi ciąg, to pierwszy też. Definiujemy ciąg
Jeśli umiemy posortować drugi ciąg, to pierwszy też. Definiujemy ciąg 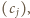 przyjmując, że
przyjmując, że 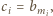 gdzie
gdzie 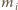 oznacza tę liczbę spośród
oznacza tę liczbę spośród 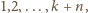 dla której różnica
dla której różnica 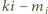 jest podzielna przez
jest podzielna przez 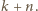 Ponieważ
Ponieważ 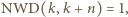 więc ciąg
więc ciąg 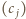 to permutacja ciągu
to permutacja ciągu 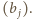 Ruchy w ciągu
Ruchy w ciągu 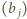 odpowiadają zamianie kolejnych wyrazów ciągu
odpowiadają zamianie kolejnych wyrazów ciągu 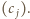 Do ciągu
Do ciągu 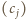 można zastosować sortowanie bąbelkowe pozwalające ustawić jego wyrazy w dowolnej kolejności.
można zastosować sortowanie bąbelkowe pozwalające ustawić jego wyrazy w dowolnej kolejności.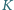 do innego koszyka
do innego koszyka 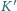 ; musi być przy tym spełniony warunek, że łączna waga kamieni w koszyku
; musi być przy tym spełniony warunek, że łączna waga kamieni w koszyku 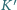 po wykonaniu ruchu jest mniejsza niż łączna waga kamieni w koszyku
po wykonaniu ruchu jest mniejsza niż łączna waga kamieni w koszyku 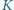 przed wykonaniem ruchu. Czy ciąg ruchów może być nieskończony?
przed wykonaniem ruchu. Czy ciąg ruchów może być nieskończony?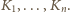 Niech
Niech 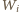 będzie wagą koszyka
będzie wagą koszyka 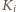 (tj. łączną wagą kamieni w tym koszyku) w ustalonej chwili. W kolejnym ruchu przekładamy kamień z koszyka
(tj. łączną wagą kamieni w tym koszyku) w ustalonej chwili. W kolejnym ruchu przekładamy kamień z koszyka 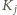 do koszyka
do koszyka 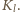 Niech
Niech  będzie wagą tego kamienia; postulowany warunek:
będzie wagą tego kamienia; postulowany warunek: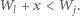
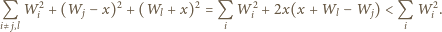
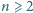 i
i 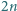 -kąt foremny. Każdy jego wierzchołek pomalowano na czerwono lub niebiesko, przy czym liczba czerwonych wierzchołków jest równa liczbie niebieskich wierzchołków. Udowodnić, że liczba głównych (przechodzących przez środek symetrii wielokąta) przekątnych o dwóch czerwonych końcach jest równa liczbie głównych przekątnych o dwóch niebieskich końcach.
-kąt foremny. Każdy jego wierzchołek pomalowano na czerwono lub niebiesko, przy czym liczba czerwonych wierzchołków jest równa liczbie niebieskich wierzchołków. Udowodnić, że liczba głównych (przechodzących przez środek symetrii wielokąta) przekątnych o dwóch czerwonych końcach jest równa liczbie głównych przekątnych o dwóch niebieskich końcach.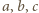 oznaczają liczbę głównych przekątnych odpowiednio o dwóch końcach czerwonych, o dwóch końcach niebieskich i o końcach w różnych kolorach. Ponieważ każdy wierzchołek jest końcem dokładnie jednej głównej przekątnej, więc mamy
oznaczają liczbę głównych przekątnych odpowiednio o dwóch końcach czerwonych, o dwóch końcach niebieskich i o końcach w różnych kolorach. Ponieważ każdy wierzchołek jest końcem dokładnie jednej głównej przekątnej, więc mamy 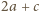 czerwonych wierzchołków i
czerwonych wierzchołków i 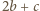 niebieskich. Ponieważ liczby te są równe, otrzymujemy
niebieskich. Ponieważ liczby te są równe, otrzymujemy