Okrągły stół i trójkąty»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu Okrągły stół i trójkąty
- Publikacja w Delcie: grudzień 2016
- Publikacja elektroniczna: 30 listopada 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (62 KB)
Wykaż, że w każdym turnieju istnieje zwycięzca lub istnieje trójkąt.
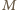będzie zawodnikiem, który wygrał maksymalną liczbę meczów. Jeśli wygrał wszystkie, jest zwycięzcą. W przeciwnym wypadku istnieje zawodnik 
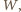który wygrał z 
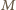oraz istnieje przynajmniej jeden zawodnik pokonany przez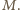 
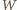zwyciężył ze wszystkimi, którzy przegrali z 
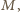to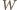 
wygrałby więcej meczów niż 
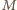(bo pokonał też 
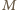) - sprzeczność. Zatem 
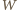przegrał z którymś z graczy, z którymi wygrał 
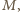czyli istnieje trójkąt.