Udowodnimy, że 
Oznaczmy krótko 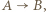 jeżeli zawodnik
jeżeli zawodnik 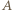 wygrał z zawodnikiem
wygrał z zawodnikiem 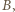 a trójkę zawodników
a trójkę zawodników 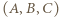 o tej własności, że
o tej własności, że 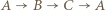 nazwijmy remisową (trójki
nazwijmy remisową (trójki 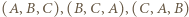 utożsamiamy).
utożsamiamy).
Rozważmy turniej szachowy z udziałem zawodników 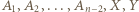 o następujących wynikach:
o następujących wynikach:
Wówczas
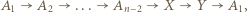
więc opisany turniej spełnia założenia zadania (zawodnicy mogą usiąść przy okrągłym stole w określonej powyżej kolejności). W takim turnieju są dokładnie 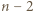 trójki remisowe, mianowicie
trójki remisowe, mianowicie 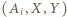 dla
dla 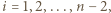 co oznacza, że
co oznacza, że 
Dowód nierówności 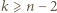 przeprowadzimy indukcyjnie. Dla
przeprowadzimy indukcyjnie. Dla 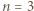 jest dokładnie jedna trójka remisowa. Przypuśćmy, że liczba trójek remisowych w turnieju z
jest dokładnie jedna trójka remisowa. Przypuśćmy, że liczba trójek remisowych w turnieju z  zawodnikami (których można odpowiednio usadzić przy okrągłym stole) jest nie mniejsza od
zawodnikami (których można odpowiednio usadzić przy okrągłym stole) jest nie mniejsza od 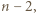 przy czym
przy czym 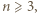 i rozważmy dowolny turniej z
i rozważmy dowolny turniej z 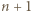 zawodnikami
zawodnikami 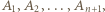 w którym
w którym
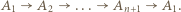
Jeżeli 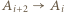 dla każdego
dla każdego 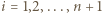 (gdzie
(gdzie 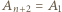 oraz
oraz 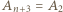 ), to każda z trójek
), to każda z trójek 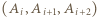 jest remisowa, więc jest ich co najmniej
jest remisowa, więc jest ich co najmniej 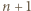 (w szczególności więcej niż
(w szczególności więcej niż 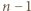 ).
).
W przeciwnym przypadku istnieje takie 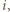 że
że 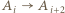 ; bez straty ogólności (ewentualnie cyklicznie przenumerowując zawodników) przypuśćmy, że
; bez straty ogólności (ewentualnie cyklicznie przenumerowując zawodników) przypuśćmy, że 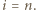 Wówczas z założenia indukcyjnego wynika, że
Wówczas z założenia indukcyjnego wynika, że 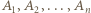 tworzą co najmniej
tworzą co najmniej 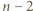 różne trójki remisowe. Wystarczy więc wykazać, że istnieje trójka remisowa, do której należy zawodnik
różne trójki remisowe. Wystarczy więc wykazać, że istnieje trójka remisowa, do której należy zawodnik 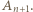 Istotnie, skoro
Istotnie, skoro 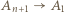 oraz
oraz 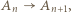 to istnieje takie
to istnieje takie 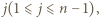 że
że
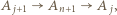
na przykład 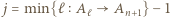 i trójka
i trójka 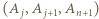 jest wówczas remisowa. To kończy dowód indukcyjny i rozwiązanie zadania.
jest wówczas remisowa. To kończy dowód indukcyjny i rozwiązanie zadania.
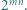
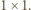 Zbiór czarnych kwadratów
Zbiór czarnych kwadratów 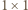 jest podzbiorem zbioru wszystkich
jest podzbiorem zbioru wszystkich 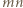 kwadratów
kwadratów 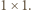
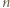 zawodników
zawodników 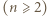 rozegrała dokładnie jeden mecz i nie było remisów.
rozegrała dokładnie jeden mecz i nie było remisów.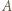 jest mistrzem, jeśli dla każdego zawodnika
jest mistrzem, jeśli dla każdego zawodnika 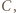 z którym
z którym 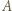 przegrał, istnieje zawodnik
przegrał, istnieje zawodnik 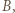 który przegrał z
który przegrał z 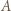 i wygrał z
i wygrał z 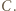 Innymi słowy, mistrz to zawodnik, który wygrał z każdym innym bezpośrednio lub pośrednio.
Innymi słowy, mistrz to zawodnik, który wygrał z każdym innym bezpośrednio lub pośrednio. -turnieju istnieje co najmniej jeden mistrz.
-turnieju istnieje co najmniej jeden mistrz.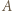 będzie dowolnym zawodnikiem, który wygrał najwięcej meczów. Udowodnimy, że
będzie dowolnym zawodnikiem, który wygrał najwięcej meczów. Udowodnimy, że 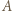 jest mistrzem.
jest mistrzem.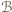 zbiór zawodników, którzy przegrali z
zbiór zawodników, którzy przegrali z 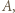 a przez
a przez 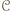 zbiór zawodników, którzy wygrali z
zbiór zawodników, którzy wygrali z 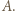 Jeżeli zbiór
Jeżeli zbiór 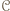 jest pusty, to
jest pusty, to 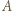 wygrał ze wszystkimi bezpośrednio, więc jest mistrzem.
wygrał ze wszystkimi bezpośrednio, więc jest mistrzem.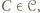 który wygrał z każdym zawodnikiem z
który wygrał z każdym zawodnikiem z 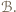 Wówczas
Wówczas 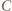 wygrał ze wszystkimi zawodnikami pokonanymi przez
wygrał ze wszystkimi zawodnikami pokonanymi przez 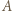 oraz z samym
oraz z samym 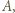 więc ma na koncie więcej zwycięstw niż
więc ma na koncie więcej zwycięstw niż 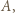 a to przeczy wyborowi zawodnika
a to przeczy wyborowi zawodnika 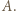 Wobec tego dla każdego
Wobec tego dla każdego 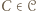 istnieje
istnieje 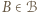 o tej własności, że
o tej własności, że 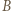 wygrał z
wygrał z 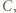 a to oznacza, że
a to oznacza, że 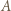 jest mistrzem.
jest mistrzem.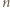 zawodników
zawodników 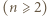 rozegrała dokładnie jeden mecz i nie było remisów.
rozegrała dokładnie jeden mecz i nie było remisów.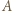 jest mistrzem, jeśli dla każdego zawodnika
jest mistrzem, jeśli dla każdego zawodnika 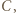 z którym
z którym 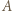 przegrał, istnieje zawodnik
przegrał, istnieje zawodnik 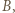 który przegrał z
który przegrał z 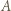 i wygrał z
i wygrał z 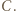 Innymi słowy, mistrz to zawodnik, który wygrał z każdym innym bezpośrednio lub pośrednio.
Innymi słowy, mistrz to zawodnik, który wygrał z każdym innym bezpośrednio lub pośrednio.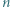 -turnieju, w którym jest dokładnie dwóch mistrzów.
-turnieju, w którym jest dokładnie dwóch mistrzów.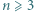 istnieje
istnieje 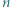 -turniej, w którym jest dokładnie trzech mistrzów.
-turniej, w którym jest dokładnie trzech mistrzów. -turnieju jest dokładnie dwóch mistrzów i oznaczmy ich przez
-turnieju jest dokładnie dwóch mistrzów i oznaczmy ich przez 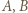 w taki sposób, że
w taki sposób, że 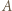 wygrał z
wygrał z 
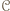 będzie zbiorem zawodników, którzy wygrali z
będzie zbiorem zawodników, którzy wygrali z 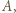 a
a 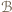 - zbiorem zawodników, którzy przegrali z
- zbiorem zawodników, którzy przegrali z 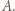 Skoro
Skoro 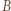 jest mistrzem oraz
jest mistrzem oraz 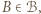 to istnieje zawodnik pokonany przez
to istnieje zawodnik pokonany przez 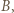 który wygrał z
który wygrał z 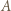 - wynika stąd w szczególności, że zbiór
- wynika stąd w szczególności, że zbiór 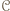 jest niepusty.
jest niepusty.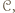 możemy na mocy poprzedniego zadania wskazać zawodnika
możemy na mocy poprzedniego zadania wskazać zawodnika 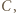 który jest mistrzem w zbiorze
który jest mistrzem w zbiorze 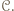 Zawodnik
Zawodnik 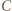 wygrał pośrednio lub bezpośrednio ze wszystkimi pozostałymi zawodnikami w
wygrał pośrednio lub bezpośrednio ze wszystkimi pozostałymi zawodnikami w 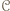 oraz wygrał bezpośrednio z
oraz wygrał bezpośrednio z 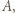 więc wygrał pośrednio ze wszystkimi zawodnikami w
więc wygrał pośrednio ze wszystkimi zawodnikami w 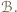 To oznacza, że
To oznacza, że 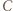 jest mistrzem w całym turnieju, co przeczy założeniu, że mistrzów jest dokładnie dwóch.
jest mistrzem w całym turnieju, co przeczy założeniu, że mistrzów jest dokładnie dwóch.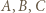 są takimi zawodnikami, że
są takimi zawodnikami, że 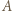 wygrał z
wygrał z 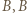 wygrał z
wygrał z 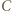 oraz
oraz 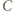 wygrał z
wygrał z 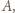 a każdy z pozostałych
a każdy z pozostałych 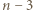 zawodników przegrał z każdym spośród
zawodników przegrał z każdym spośród 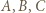 (wyniki meczów pomiędzy tymi
(wyniki meczów pomiędzy tymi 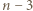 zawodnikami mogą być dowolne). W tym turnieju
zawodnikami mogą być dowolne). W tym turnieju 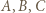 są jedynymi mistrzami (nikt z pozostałych nie wygrał z żadnym z nich) i jest ich trzech.
są jedynymi mistrzami (nikt z pozostałych nie wygrał z żadnym z nich) i jest ich trzech.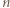 zawodników
zawodników 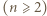 rozegrała dokładnie jeden mecz i nie było remisów.
rozegrała dokładnie jeden mecz i nie było remisów.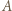 jest mistrzem, jeśli dla każdego zawodnika
jest mistrzem, jeśli dla każdego zawodnika 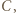 z którym
z którym 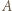 przegrał, istnieje zawodnik
przegrał, istnieje zawodnik 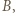 który przegrał z
który przegrał z 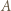 i wygrał z
i wygrał z 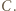 Innymi słowy, mistrz to zawodnik, który wygrał z każdym innym bezpośrednio lub pośrednio.
Innymi słowy, mistrz to zawodnik, który wygrał z każdym innym bezpośrednio lub pośrednio.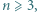 dla których istnieje
dla których istnieje 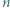 -turniej, w którym każdy jest mistrzem.
-turniej, w którym każdy jest mistrzem.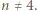
 -turniej, w którym każdy jest mistrzem. Udowodnimy, że jeśli istnieje mistrzowski
-turniej, w którym każdy jest mistrzem. Udowodnimy, że jeśli istnieje mistrzowski  -turniej, to istnieje mistrzowski
-turniej, to istnieje mistrzowski 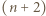 -turniej.
-turniej.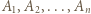 będą zawodnikami pewnego mistrzowskiego
będą zawodnikami pewnego mistrzowskiego 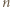 -turnieju, a
-turnieju, a 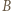 i
i 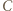 takimi dwoma dodatkowymi zawodnikami, że
takimi dwoma dodatkowymi zawodnikami, że 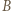 wygrał z
wygrał z 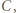 a ponadto
a ponadto 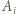 wygrał z
wygrał z 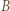 i przegrał z
i przegrał z 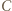 dla każdego
dla każdego 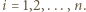 Wówczas
Wówczas 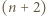 -turniej powstały przez dołączenie zawodników
-turniej powstały przez dołączenie zawodników 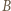 i
i 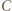 jest mistrzowski.
jest mistrzowski.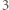 -turniej złożony z zawodników
-turniej złożony z zawodników 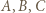 takich, że
takich, że 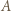 wygrał z
wygrał z 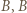 wygrał z
wygrał z 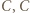 wygrał z
wygrał z 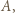 oraz
oraz 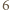 -turniej pokazany na poniższym rysunku (punkty oznaczają zawodników, a strzałka z
-turniej pokazany na poniższym rysunku (punkty oznaczają zawodników, a strzałka z 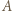 do
do 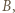 że
że 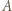 wygrał z
wygrał z 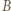 ) są mistrzowskie. W połączeniu z konkluzją poprzednich dwóch akapitów prowadzi to do wniosku, że
) są mistrzowskie. W połączeniu z konkluzją poprzednich dwóch akapitów prowadzi to do wniosku, że  -turniej mistrzowski istnieje dla każdej liczby nieparzystej
-turniej mistrzowski istnieje dla każdej liczby nieparzystej 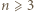 oraz dla każdej liczby parzystej
oraz dla każdej liczby parzystej 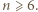
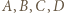 w taki sposób, że
w taki sposób, że 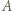 wygrał z
wygrał z 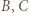 wygrał z
wygrał z 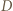 oraz (bez straty ogólności)
oraz (bez straty ogólności) 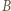 wygrał z
wygrał z 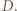 Wówczas, skoro
Wówczas, skoro 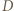 jest mistrzem, to
jest mistrzem, to 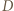 musiał pośrednio wygrać z
musiał pośrednio wygrać z 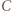 - jedyna możliwość jest taka, że
- jedyna możliwość jest taka, że 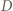 wygrał z
wygrał z 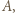 a
a 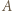 wygrał z
wygrał z 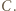 Jednak wówczas ten z zawodników
Jednak wówczas ten z zawodników 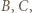 który przegrał mecz między nimi, nie miał jak wygrać pośrednio z tym drugim - sprzeczność.
który przegrał mecz między nimi, nie miał jak wygrać pośrednio z tym drugim - sprzeczność. punktów białych oraz
punktów białych oraz 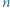 punktów czarnych. Białe punkty są ponumerowane liczbami od 1 do
punktów czarnych. Białe punkty są ponumerowane liczbami od 1 do 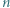 zgodnie z ruchem wskazówek zegara, a czarne punkty są ponumerowane liczbami od 1 do
zgodnie z ruchem wskazówek zegara, a czarne punkty są ponumerowane liczbami od 1 do 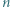 przeciwnie do ruchu wskazówek zegara. Wykazać, że ten okrąg można rozciąć na dwa łuki o tej własności, że każdy numer od 1 do
przeciwnie do ruchu wskazówek zegara. Wykazać, że ten okrąg można rozciąć na dwa łuki o tej własności, że każdy numer od 1 do 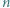 pojawia się dokładnie raz na każdym z nich.
pojawia się dokładnie raz na każdym z nich.
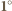 Pomiędzy punktami o numerze 1 znajdują się punkty białe o numerach od 2 do
Pomiędzy punktami o numerze 1 znajdują się punkty białe o numerach od 2 do 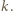 Wówczas wybierając jeden punkt podziału okręgu na łuki pomiędzy białymi punktami o numerach
Wówczas wybierając jeden punkt podziału okręgu na łuki pomiędzy białymi punktami o numerach 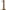 i
i 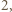 a drugi - w taki sposób, aby na obydwu uzyskanych łukach było po
a drugi - w taki sposób, aby na obydwu uzyskanych łukach było po  wyróżnionych punktów, uzyskujemy rozcięcie o postulowanej własności.
wyróżnionych punktów, uzyskujemy rozcięcie o postulowanej własności.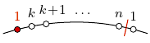
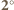 Pomiędzy punktami o numerze
Pomiędzy punktami o numerze 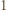 znajdują się punkty białe o numerach od
znajdują się punkty białe o numerach od 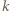 do
do 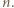 Wówczas wybierając jeden punkt podziału okręgu na łuki pomiędzy białymi punktami o numerach
Wówczas wybierając jeden punkt podziału okręgu na łuki pomiędzy białymi punktami o numerach 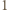 i
i 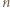 (a drugi odpowiednio jak wyżej), uzyskujemy rozcięcie spełniające warunki zadania.
(a drugi odpowiednio jak wyżej), uzyskujemy rozcięcie spełniające warunki zadania.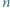 oraz zbiór
oraz zbiór 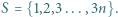 Wyznaczyć największą możliwą liczbę elementów podzbioru
Wyznaczyć największą możliwą liczbę elementów podzbioru 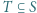 o następującej własności: Dla każdej trójki (niekoniecznie różnych) elementów
o następującej własności: Dla każdej trójki (niekoniecznie różnych) elementów 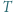 ich suma nie należy do
ich suma nie należy do 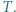
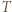 jest równa
jest równa 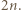
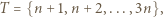
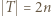 oraz suma każdych trzech elementów
oraz suma każdych trzech elementów 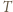 jest większa od
jest większa od 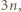 a zatem nie należy do
a zatem nie należy do 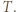
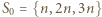 oraz
oraz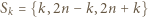
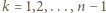 ) stanowią rozbicie zbioru
) stanowią rozbicie zbioru 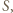 a w każdym z nich jeden z elementów jest sumą trzech innych, mianowicie
a w każdym z nich jeden z elementów jest sumą trzech innych, mianowicie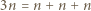
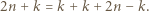
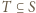 oraz
oraz 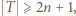 to
to 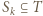 dla pewnego
dla pewnego 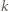 i w konsekwencji zbiór
i w konsekwencji zbiór 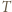 nie ma danej w treści zadania własności.
nie ma danej w treści zadania własności.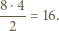
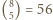 piątek osób są co najmniej trzy znajomości, a każda taka trójka znających się nawzajem osób należy do dokładnie
piątek osób są co najmniej trzy znajomości, a każda taka trójka znających się nawzajem osób należy do dokładnie 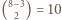 piątek osób. Wobec tego łączna liczba znajomości w grupie jest nie mniejsza od
piątek osób. Wobec tego łączna liczba znajomości w grupie jest nie mniejsza od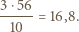
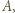 która ma co najmniej
która ma co najmniej 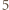 znajomych. Aby zakończyć rozwiązanie, wystarczy stwierdzić, że wśród znajomych osoby
znajomych. Aby zakończyć rozwiązanie, wystarczy stwierdzić, że wśród znajomych osoby 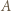 pewnych trzech zna się wzajemnie, więc dołączając do nich
pewnych trzech zna się wzajemnie, więc dołączając do nich 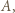 otrzymujemy czwórkę osób o postulowanej własności.
otrzymujemy czwórkę osób o postulowanej własności.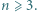 W każde pole kwadratowej planszy
W każde pole kwadratowej planszy 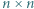 wpisujemy jedną z liczb
wpisujemy jedną z liczb 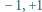 tak, że suma wszystkich wpisanych liczb wynosi 1. Wyznaczamy sumę liczb w każdym wierszu oraz sumę liczb w każdej kolumnie; dostajemy ciąg
tak, że suma wszystkich wpisanych liczb wynosi 1. Wyznaczamy sumę liczb w każdym wierszu oraz sumę liczb w każdej kolumnie; dostajemy ciąg 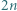 liczb nieparzystych. Ile maksymalnie może być w tym ciągu liczb ujemnych?
liczb nieparzystych. Ile maksymalnie może być w tym ciągu liczb ujemnych?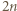 sum (wierszy i kolumn) może więc być co najwyżej
sum (wierszy i kolumn) może więc być co najwyżej 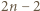 liczb ujemnych.
liczb ujemnych.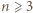 ta wartość jest osiągalna. Ilustracja przedstawia przykładową realizację, gdy
ta wartość jest osiągalna. Ilustracja przedstawia przykładową realizację, gdy 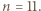 Opis algorytmu: cały skrajny dolny wiersz oraz całą skrajną prawą kolumnę wypełniamy jedynkami. Po odcięciu tego fragmentu zostaje plansza kwadratowa o boku długości parzystej
Opis algorytmu: cały skrajny dolny wiersz oraz całą skrajną prawą kolumnę wypełniamy jedynkami. Po odcięciu tego fragmentu zostaje plansza kwadratowa o boku długości parzystej 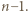 W jej górnym wierszu umieszczamy, kolejno od lewej,
W jej górnym wierszu umieszczamy, kolejno od lewej, 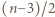 jedynek oraz
jedynek oraz 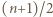 minus jedynek. W kolejnych wierszach (planszy
minus jedynek. W kolejnych wierszach (planszy 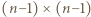 ) powtarzamy ten układ z przesunięciem (w każdym kroku) o jednostkę w prawo; nadwyżkę wychodzącą poza prawy skraj przenosimy przy tym cyklicznie na skrajne lewe pole.
) powtarzamy ten układ z przesunięciem (w każdym kroku) o jednostkę w prawo; nadwyżkę wychodzącą poza prawy skraj przenosimy przy tym cyklicznie na skrajne lewe pole.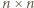 uzyskujemy przewagę minusów nad plusami we wszystkich wierszach i kolumnach z wyjątkiem ostatniego i ostatniej. Każdy z początkowych
uzyskujemy przewagę minusów nad plusami we wszystkich wierszach i kolumnach z wyjątkiem ostatniego i ostatniej. Każdy z początkowych 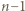 wierszy ma sumę
wierszy ma sumę 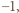 zaś ostatni wiersz ma sumę
zaś ostatni wiersz ma sumę 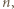 zatem suma całej tabeli wynosi 1. Stąd, ostatecznie, odpowiedź: szukane maksimum wynosi
zatem suma całej tabeli wynosi 1. Stąd, ostatecznie, odpowiedź: szukane maksimum wynosi 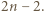
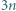 kamieni na szachownicy
kamieni na szachownicy 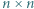 w taki sposób, aby w każdym wierszu i w każdej kolumnie znalazły się dokładnie trzy kamienie i były one rozłożone na co najwyżej dwóch polach?
w taki sposób, aby w każdym wierszu i w każdej kolumnie znalazły się dokładnie trzy kamienie i były one rozłożone na co najwyżej dwóch polach?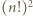 sposobów.
sposobów. pól szachownicy po jednym w każdym rzędzie - rozsypem. Rozsyp można wybrać na dokładnie
pól szachownicy po jednym w każdym rzędzie - rozsypem. Rozsyp można wybrać na dokładnie 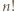 sposobów (np. w
sposobów (np. w 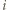 -tym wierszu wybieramy na
-tym wierszu wybieramy na 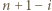 sposobów kolumnę, do której należy pole).
sposobów kolumnę, do której należy pole).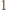 lub
lub 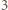 kamienie, jak i zbiór pól zawierających
kamienie, jak i zbiór pól zawierających 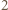 lub
lub 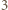 kamienie, jest rozsypem. To oznacza, że z każdym rozłożeniem kamieni można związać (uporządkowaną) parę rozsypów.
kamienie, jest rozsypem. To oznacza, że z każdym rozłożeniem kamieni można związać (uporządkowaną) parę rozsypów.
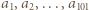 i rozważmy sumy
i rozważmy sumy 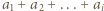 dla
dla 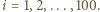 Są to dodatnie liczby całkowite mniejsze od 300. Jeśli któraś z tych sum jest równa 200, zadanie jest rozwiązane, podobnie dla sumy 100 (wtedy wszystkie pozostałe
Są to dodatnie liczby całkowite mniejsze od 300. Jeśli któraś z tych sum jest równa 200, zadanie jest rozwiązane, podobnie dla sumy 100 (wtedy wszystkie pozostałe 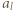 wyznaczają szukany łuk).
wyznaczają szukany łuk).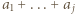 oraz
oraz 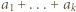 dla
dla 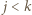 dają taką samą resztę, więc ich różnica
dają taką samą resztę, więc ich różnica 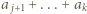 dzieli się przez 100, czyli jest równa 200 lub 100. Podobnie jak powyżej wyznacza ona wobec tego poszukiwany łuk lub jego dopełnienie.
dzieli się przez 100, czyli jest równa 200 lub 100. Podobnie jak powyżej wyznacza ona wobec tego poszukiwany łuk lub jego dopełnienie.
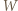 stoi za niższym
stoi za niższym 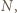 wbrew żądaniu, że mają stać według wzrostu. Rozważmy żołnierzy stojących w rzędzie z
wbrew żądaniu, że mają stać według wzrostu. Rozważmy żołnierzy stojących w rzędzie z 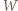 i przed nim (są oni wyżsi od niego, ich wraz z
i przed nim (są oni wyżsi od niego, ich wraz z 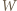 nazwiemy wysokimi) oraz żołnierzy stojących w rzędzie z
nazwiemy wysokimi) oraz żołnierzy stojących w rzędzie z 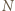 i za nim (są niżsi od
i za nim (są niżsi od 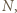 ich wraz z
ich wraz z 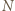 nazwiemy niskimi). Zauważmy, że każdy żołnierz wysoki jest wyższy od każdego z żołnierzy niskich (bo jest wyższy od
nazwiemy niskimi). Zauważmy, że każdy żołnierz wysoki jest wyższy od każdego z żołnierzy niskich (bo jest wyższy od 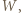 a
a 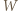 - od
- od 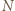 ). Wysokich i niskich żołnierzy jest łącznie o 1 więcej niż kolumn, więc zanim uporządkowano rzędy, pewnych dwóch z nich stało w tej samej kolumnie. Wysocy stali w różnych kolumnach, niscy też w różnych, stąd w jednej kolumnie musiał stać jakiś żołnierz wysoki za niskim - sprzeczność, bo kolumny były już wtedy uporządkowane.
). Wysokich i niskich żołnierzy jest łącznie o 1 więcej niż kolumn, więc zanim uporządkowano rzędy, pewnych dwóch z nich stało w tej samej kolumnie. Wysocy stali w różnych kolumnach, niscy też w różnych, stąd w jednej kolumnie musiał stać jakiś żołnierz wysoki za niskim - sprzeczność, bo kolumny były już wtedy uporządkowane.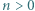 istnieje taka liczba całkowita
istnieje taka liczba całkowita 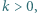 że liczbę
że liczbę 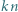 można zapisać w systemie dziesiętnym używając wyłącznie cyfr 0 i 1.
można zapisać w systemie dziesiętnym używając wyłącznie cyfr 0 i 1.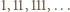 Wśród pierwszych
Wśród pierwszych 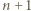 z nich pewne dwie dają tę samą resztę z dzielenia przez
z nich pewne dwie dają tę samą resztę z dzielenia przez 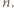 Ich różnica jest liczbą postaci
Ich różnica jest liczbą postaci 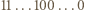 podzielną przez
podzielną przez 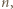 co kończy dowód.
co kończy dowód.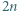 zawodników
zawodników 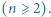 Chcemy zaplanować rozgrywki składające się z
Chcemy zaplanować rozgrywki składające się z 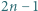 rund w taki sposób, aby każdy zawodnik rozegrał w każdej rundzie dokładnie jedną partię oraz tak, aby w całym turnieju każdy zawodnik zagrał z każdym innym zawodnikiem dokładnie raz. Wyznaczyć wszystkie dodatnie liczby całkowite
rund w taki sposób, aby każdy zawodnik rozegrał w każdej rundzie dokładnie jedną partię oraz tak, aby w całym turnieju każdy zawodnik zagrał z każdym innym zawodnikiem dokładnie raz. Wyznaczyć wszystkie dodatnie liczby całkowite 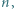 dla których jest to możliwe.
dla których jest to możliwe.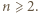
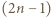 -kątny o podstawie
-kątny o podstawie 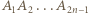 i wierzchołku
i wierzchołku 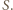 Ponumerujmy zawodników liczbami od
Ponumerujmy zawodników liczbami od 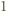 do
do 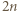 i ustalmy, że zawodnik o numerze
i ustalmy, że zawodnik o numerze 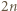 w
w 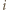 -tej rundzie gra z zawodnikiem o numerze
-tej rundzie gra z zawodnikiem o numerze 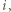 a dla
a dla 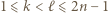 zawodnicy o numerach
zawodnicy o numerach 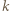 i
i 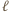 grają ze sobą w
grają ze sobą w 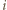 -tej rundzie wtedy i tylko wtedy, gdy
-tej rundzie wtedy i tylko wtedy, gdy 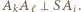
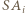 ) oraz każda runda składa się z dokładnie
) oraz każda runda składa się z dokładnie 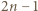 partii.
partii. zawodników
zawodników 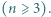 Każdy zawodnik rozegrał z każdym innym zawodnikiem dokładnie jedną partię, przy czym żadna partia nie zakończyła się remisem. Po turnieju wszyscy zawodnicy usiedli przy okrągłym stole w taki sposób, że każdy zawodnik wygrał z osobą siedzącą obok niego z jego lewej strony. Wyznaczyć, w zależności od
Każdy zawodnik rozegrał z każdym innym zawodnikiem dokładnie jedną partię, przy czym żadna partia nie zakończyła się remisem. Po turnieju wszyscy zawodnicy usiedli przy okrągłym stole w taki sposób, że każdy zawodnik wygrał z osobą siedzącą obok niego z jego lewej strony. Wyznaczyć, w zależności od 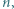 największą liczbę
największą liczbę 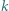 o następującej własności: istnieje (niezależnie od przebiegu turnieju) co najmniej
o następującej własności: istnieje (niezależnie od przebiegu turnieju) co najmniej 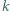 różnych takich trójek zawodników
różnych takich trójek zawodników 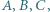 że
że 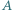 wygrał z
wygrał z 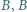 wygrał z
wygrał z 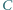 oraz
oraz 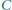 wygrał z
wygrał z 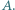

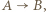 jeżeli zawodnik
jeżeli zawodnik 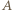 wygrał z zawodnikiem
wygrał z zawodnikiem 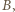 a trójkę zawodników
a trójkę zawodników 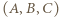 o tej własności, że
o tej własności, że 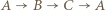 nazwijmy remisową (trójki
nazwijmy remisową (trójki 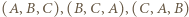 utożsamiamy).
utożsamiamy).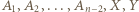 o następujących wynikach:
o następujących wynikach: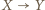 ;
;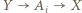 dla
dla 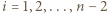 ;
;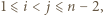 to
to 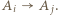
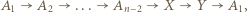
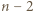 trójki remisowe, mianowicie
trójki remisowe, mianowicie 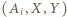 dla
dla 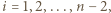 co oznacza, że
co oznacza, że 
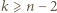 przeprowadzimy indukcyjnie. Dla
przeprowadzimy indukcyjnie. Dla 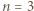 jest dokładnie jedna trójka remisowa. Przypuśćmy, że liczba trójek remisowych w turnieju z
jest dokładnie jedna trójka remisowa. Przypuśćmy, że liczba trójek remisowych w turnieju z  zawodnikami (których można odpowiednio usadzić przy okrągłym stole) jest nie mniejsza od
zawodnikami (których można odpowiednio usadzić przy okrągłym stole) jest nie mniejsza od 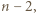 przy czym
przy czym 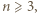 i rozważmy dowolny turniej z
i rozważmy dowolny turniej z 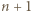 zawodnikami
zawodnikami 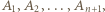 w którym
w którym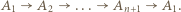
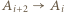 dla każdego
dla każdego 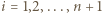 (gdzie
(gdzie 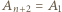 oraz
oraz 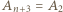 ), to każda z trójek
), to każda z trójek 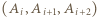 jest remisowa, więc jest ich co najmniej
jest remisowa, więc jest ich co najmniej 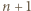 (w szczególności więcej niż
(w szczególności więcej niż 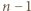 ).
).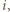 że
że 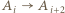 ; bez straty ogólności (ewentualnie cyklicznie przenumerowując zawodników) przypuśćmy, że
; bez straty ogólności (ewentualnie cyklicznie przenumerowując zawodników) przypuśćmy, że 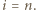 Wówczas z założenia indukcyjnego wynika, że
Wówczas z założenia indukcyjnego wynika, że 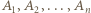 tworzą co najmniej
tworzą co najmniej 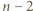 różne trójki remisowe. Wystarczy więc wykazać, że istnieje trójka remisowa, do której należy zawodnik
różne trójki remisowe. Wystarczy więc wykazać, że istnieje trójka remisowa, do której należy zawodnik 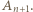 Istotnie, skoro
Istotnie, skoro 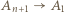 oraz
oraz 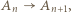 to istnieje takie
to istnieje takie 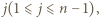 że
że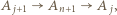
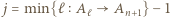 i trójka
i trójka 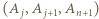 jest wówczas remisowa. To kończy dowód indukcyjny i rozwiązanie zadania.
jest wówczas remisowa. To kończy dowód indukcyjny i rozwiązanie zadania. zawodników
zawodników 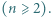 Każdy zawodnik rozegrał z każdym innym zawodnikiem dokładnie jedną partię, przy czym żadna partia nie zakończyła się remisem. Niech
Każdy zawodnik rozegrał z każdym innym zawodnikiem dokładnie jedną partię, przy czym żadna partia nie zakończyła się remisem. Niech 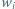 oraz
oraz 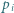 będą odpowiednio liczbami zwycięstw i porażek
będą odpowiednio liczbami zwycięstw i porażek 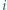 -tego gracza, gdzie
-tego gracza, gdzie 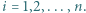 Wykazać, że
Wykazać, że
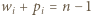 dla każdego
dla każdego 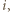 a także
a także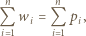
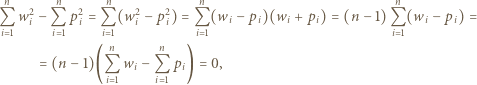
 i
i 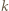 kulek, przecinamy wszystkie
kulek, przecinamy wszystkie 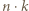 nitek pomiędzy rozdzielanymi kulkami. Kulki pozostające w jednej grupie nadal są połączone. W efekcie, po uzyskaniu pojedynczych kulek, przetniemy wszystkie nitki (i każdą tylko raz), a rozważana suma iloczynów to właśnie liczba tych nitek.
nitek pomiędzy rozdzielanymi kulkami. Kulki pozostające w jednej grupie nadal są połączone. W efekcie, po uzyskaniu pojedynczych kulek, przetniemy wszystkie nitki (i każdą tylko raz), a rozważana suma iloczynów to właśnie liczba tych nitek.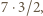 bo w każdym z nich uczestniczą dwie osoby. Jednak liczba ta nie jest całkowita.
bo w każdym z nich uczestniczą dwie osoby. Jednak liczba ta nie jest całkowita.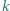 chłopców z tej grupy zna "wspólnymi siłami" co najmniej
chłopców z tej grupy zna "wspólnymi siłami" co najmniej 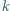 dziewcząt.
dziewcząt.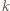 chłopców podaje dziewczętom łącznie
chłopców podaje dziewczętom łącznie 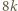 kończyn. Jednocześnie każde dziewczę jest w stanie chwycić najwyżej 8 z nich, znajomych dziewczyn musi więc być co najmniej
kończyn. Jednocześnie każde dziewczę jest w stanie chwycić najwyżej 8 z nich, znajomych dziewczyn musi więc być co najmniej 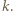
 -osobowej grupie każdy miał inną liczbę znajomych, to byłyby to liczby
-osobowej grupie każdy miał inną liczbę znajomych, to byłyby to liczby 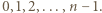 Nie jest jednak możliwe, by ktoś znał wszystkich pozostałych
Nie jest jednak możliwe, by ktoś znał wszystkich pozostałych 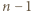 osób i jednocześnie ktoś inny miał 0 znajomych.
osób i jednocześnie ktoś inny miał 0 znajomych.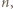 to po odwróceniu jest ich
to po odwróceniu jest ich 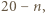 czyli tyle samo, ile wśród pozostałych monet.
czyli tyle samo, ile wśród pozostałych monet.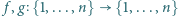 są określone wzorami
są określone wzorami
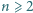 ustalić, ile jest funkcji
ustalić, ile jest funkcji 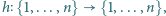 dających się wyrazić jako złożenia skończenie wielu odwzorowań, z których każde jest jedną z funkcji
dających się wyrazić jako złożenia skończenie wielu odwzorowań, z których każde jest jedną z funkcji 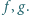 [Dopuszczamy również złożenie puste (zero egzemplarzy funkcji
[Dopuszczamy również złożenie puste (zero egzemplarzy funkcji 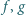 ), przyjmując zwykłą umowę, że daje ono w wyniku odwzorowanie tożsamościowe
), przyjmując zwykłą umowę, że daje ono w wyniku odwzorowanie tożsamościowe 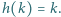 ]
]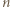 kropek na "planszy"
kropek na "planszy"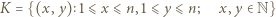
![[1,n]× [1,n]](/math/temat/matematyka/kombinatoryka/zadania/2018/02/28/zm-k44-757/3x-70d38ee30bc0c5115fe4b8c7fe268f771c7f92ce-im-66,57,43-FF,FF,FF.gif) ), po jednej kropce na każdej linii pionowej. Stosując do takiego układu funkcję
), po jednej kropce na każdej linii pionowej. Stosując do takiego układu funkcję 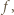 uzyskujemy przesunięcie wszystkich kropek o jednostkę w dół, z wyjątkiem tych, które już były na dolnej krawędzi; one nie zmieniają położenia. Działanie funkcji
uzyskujemy przesunięcie wszystkich kropek o jednostkę w dół, z wyjątkiem tych, które już były na dolnej krawędzi; one nie zmieniają położenia. Działanie funkcji 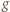 jest podobne (ruch w górę; blokada na górnej krawędzi).
jest podobne (ruch w górę; blokada na górnej krawędzi).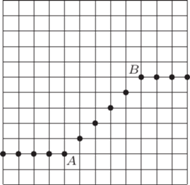
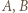 będą dwoma różnymi punktami zbioru
będą dwoma różnymi punktami zbioru 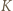 takimi, że odcinek
takimi, że odcinek 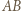 jest równoległy do przekątnej kwadratu, przy czym punkt
jest równoległy do przekątnej kwadratu, przy czym punkt 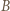 leży na prawo i w górę od
leży na prawo i w górę od 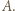 Dla takiej pary punktów niech
Dla takiej pary punktów niech 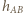 oznacza funkcję, której wykres składa się z punktów kratowych, położonych na odcinku poziomym od lewego skraja planszy do
oznacza funkcję, której wykres składa się z punktów kratowych, położonych na odcinku poziomym od lewego skraja planszy do 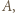 na odcinku
na odcinku 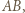 i na odcinku od
i na odcinku od 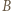 do prawego skraja planszy (rysunek obok). Złożenie takiej funkcji z dowolną z operacji
do prawego skraja planszy (rysunek obok). Złożenie takiej funkcji z dowolną z operacji 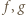 daje w wyniku znów funkcję takiej postaci lub funkcję stałą (o wykresie: wszystkie kropki na krawędzi górnej lub dolnej). Złożenie funkcji stałej z
daje w wyniku znów funkcję takiej postaci lub funkcję stałą (o wykresie: wszystkie kropki na krawędzi górnej lub dolnej). Złożenie funkcji stałej z 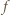 lub
lub 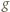 daje oczywiście także funkcję stałą.
daje oczywiście także funkcję stałą.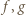 (w dowolnej kolejności) możemy uzyskać tylko funkcje typu
(w dowolnej kolejności) możemy uzyskać tylko funkcje typu 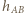 oraz funkcje stałe. Co ważne, każdą taką funkcję da się w ten sposób uzyskać (przykładową ewolucję przedstawia rysunek poniżej).
oraz funkcje stałe. Co ważne, każdą taką funkcję da się w ten sposób uzyskać (przykładową ewolucję przedstawia rysunek poniżej).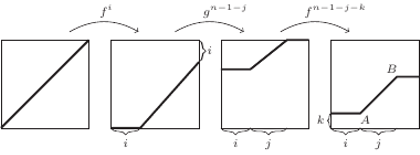
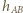 - czyli możliwe pary punktów
- czyli możliwe pary punktów 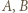 - oraz doliczyć funkcje stałe. Punkty
- oraz doliczyć funkcje stałe. Punkty 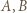 mogą leżeć na przekątnej
mogą leżeć na przekątnej 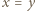 (przechodzącej przez
(przechodzącej przez 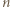 punktów kratowych), na jednej z dwóch linii
punktów kratowych), na jednej z dwóch linii 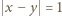 (po
(po 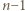 punktów kratowych), na jednej z dwóch linii
punktów kratowych), na jednej z dwóch linii 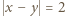 (po
(po 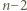 punktów kratowych), itd. Liczba możliwych do uzyskania funkcji (więc
punktów kratowych), itd. Liczba możliwych do uzyskania funkcji (więc  funkcji stałych oraz wszystkich funkcji
funkcji stałych oraz wszystkich funkcji 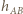 ) wynosi zatem
) wynosi zatem![2 n+(n )+2 [(n −1)+ (n −2) +...+ (2)] = n+(n )+2(n ) = n(2n--−-3n-+7)-. 2 2 2 2 2 3 6](/math/temat/matematyka/kombinatoryka/zadania/2018/02/28/zm-k44-757/12x-fe5da781f2cf49f9a749e7784cb8b36acd302625-dm-66,57,43-FF,FF,FF.gif)