a) Przypuśćmy, że w pewnym  -turnieju jest dokładnie dwóch mistrzów i oznaczmy ich przez
-turnieju jest dokładnie dwóch mistrzów i oznaczmy ich przez 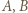 w taki sposób, że
w taki sposób, że 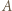 wygrał z
wygrał z 
Niech 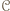 będzie zbiorem zawodników, którzy wygrali z
będzie zbiorem zawodników, którzy wygrali z 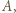 a
a 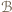 - zbiorem zawodników, którzy przegrali z
- zbiorem zawodników, którzy przegrali z 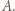 Skoro
Skoro 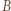 jest mistrzem oraz
jest mistrzem oraz 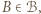 to istnieje zawodnik pokonany przez
to istnieje zawodnik pokonany przez 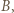 który wygrał z
który wygrał z 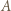 - wynika stąd w szczególności, że zbiór
- wynika stąd w szczególności, że zbiór 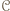 jest niepusty.
jest niepusty.
Ograniczając turniej do meczów rozegranych między zawodnikami ze zbioru 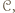 możemy na mocy poprzedniego zadania wskazać zawodnika
możemy na mocy poprzedniego zadania wskazać zawodnika 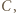 który jest mistrzem w zbiorze
który jest mistrzem w zbiorze 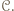 Zawodnik
Zawodnik 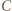 wygrał pośrednio lub bezpośrednio ze wszystkimi pozostałymi zawodnikami w
wygrał pośrednio lub bezpośrednio ze wszystkimi pozostałymi zawodnikami w 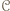 oraz wygrał bezpośrednio z
oraz wygrał bezpośrednio z 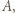 więc wygrał pośrednio ze wszystkimi zawodnikami w
więc wygrał pośrednio ze wszystkimi zawodnikami w 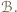 To oznacza, że
To oznacza, że 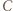 jest mistrzem w całym turnieju, co przeczy założeniu, że mistrzów jest dokładnie dwóch.
jest mistrzem w całym turnieju, co przeczy założeniu, że mistrzów jest dokładnie dwóch.
b) Rozważmy turniej, w którym 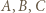 są takimi zawodnikami, że
są takimi zawodnikami, że 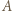 wygrał z
wygrał z 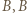 wygrał z
wygrał z 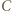 oraz
oraz 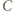 wygrał z
wygrał z 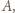 a każdy z pozostałych
a każdy z pozostałych 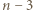 zawodników przegrał z każdym spośród
zawodników przegrał z każdym spośród 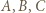 (wyniki meczów pomiędzy tymi
(wyniki meczów pomiędzy tymi 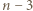 zawodnikami mogą być dowolne). W tym turnieju
zawodnikami mogą być dowolne). W tym turnieju 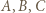 są jedynymi mistrzami (nikt z pozostałych nie wygrał z żadnym z nich) i jest ich trzech.
są jedynymi mistrzami (nikt z pozostałych nie wygrał z żadnym z nich) i jest ich trzech.
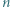 -turnieju, w którym jest dokładnie dwóch mistrzów.
-turnieju, w którym jest dokładnie dwóch mistrzów.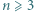 istnieje
istnieje 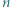 -turniej, w którym jest dokładnie trzech mistrzów.
-turniej, w którym jest dokładnie trzech mistrzów.
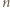 zawodników
zawodników 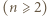 rozegrała dokładnie jeden mecz i nie było remisów.
rozegrała dokładnie jeden mecz i nie było remisów.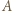 jest mistrzem, jeśli dla każdego zawodnika
jest mistrzem, jeśli dla każdego zawodnika 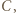 z którym
z którym 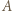 przegrał, istnieje zawodnik
przegrał, istnieje zawodnik 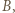 który przegrał z
który przegrał z 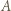 i wygrał z
i wygrał z 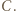 Innymi słowy, mistrz to zawodnik, który wygrał z każdym innym bezpośrednio lub pośrednio.
Innymi słowy, mistrz to zawodnik, który wygrał z każdym innym bezpośrednio lub pośrednio. -turnieju jest dokładnie dwóch mistrzów i oznaczmy ich przez
-turnieju jest dokładnie dwóch mistrzów i oznaczmy ich przez 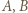 w taki sposób, że
w taki sposób, że 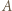 wygrał z
wygrał z 
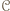 będzie zbiorem zawodników, którzy wygrali z
będzie zbiorem zawodników, którzy wygrali z 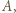 a
a 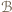 - zbiorem zawodników, którzy przegrali z
- zbiorem zawodników, którzy przegrali z 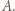 Skoro
Skoro 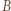 jest mistrzem oraz
jest mistrzem oraz 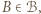 to istnieje zawodnik pokonany przez
to istnieje zawodnik pokonany przez 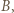 który wygrał z
który wygrał z 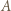 - wynika stąd w szczególności, że zbiór
- wynika stąd w szczególności, że zbiór 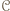 jest niepusty.
jest niepusty.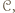 możemy na mocy poprzedniego zadania wskazać zawodnika
możemy na mocy poprzedniego zadania wskazać zawodnika 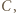 który jest mistrzem w zbiorze
który jest mistrzem w zbiorze 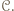 Zawodnik
Zawodnik 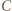 wygrał pośrednio lub bezpośrednio ze wszystkimi pozostałymi zawodnikami w
wygrał pośrednio lub bezpośrednio ze wszystkimi pozostałymi zawodnikami w 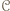 oraz wygrał bezpośrednio z
oraz wygrał bezpośrednio z 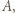 więc wygrał pośrednio ze wszystkimi zawodnikami w
więc wygrał pośrednio ze wszystkimi zawodnikami w 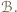 To oznacza, że
To oznacza, że 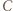 jest mistrzem w całym turnieju, co przeczy założeniu, że mistrzów jest dokładnie dwóch.
jest mistrzem w całym turnieju, co przeczy założeniu, że mistrzów jest dokładnie dwóch.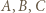 są takimi zawodnikami, że
są takimi zawodnikami, że 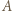 wygrał z
wygrał z 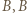 wygrał z
wygrał z 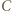 oraz
oraz 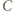 wygrał z
wygrał z 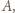 a każdy z pozostałych
a każdy z pozostałych 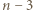 zawodników przegrał z każdym spośród
zawodników przegrał z każdym spośród 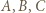 (wyniki meczów pomiędzy tymi
(wyniki meczów pomiędzy tymi 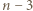 zawodnikami mogą być dowolne). W tym turnieju
zawodnikami mogą być dowolne). W tym turnieju 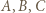 są jedynymi mistrzami (nikt z pozostałych nie wygrał z żadnym z nich) i jest ich trzech.
są jedynymi mistrzami (nikt z pozostałych nie wygrał z żadnym z nich) i jest ich trzech.