Klub 44M - zadania II 2017»Zadanie 727
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania II 2017
- Publikacja w Delcie: luty 2017
- Publikacja elektroniczna: 31 stycznia 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (155 KB)
Trójkąt równoboczny o boku długości 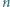 został podzielony (prostymi równoległymi do boków) na
został podzielony (prostymi równoległymi do boków) na 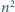 trójkącików o boku 1. Każdy wierzchołek powstałej siatki (tj. wierzchołek któregoś trójkącika) jest pomalowany na biało lub czarno. Wykonujemy ciąg ruchów. W jednym ruchu zmieniamy kolor wszystkich wierzchołków, leżących na jednej linii prostej, zawierającej bok któregoś trójkącika.
trójkącików o boku 1. Każdy wierzchołek powstałej siatki (tj. wierzchołek któregoś trójkącika) jest pomalowany na biało lub czarno. Wykonujemy ciąg ruchów. W jednym ruchu zmieniamy kolor wszystkich wierzchołków, leżących na jednej linii prostej, zawierającej bok któregoś trójkącika.
Wyznaczyć wszystkie liczby naturalne 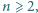 dla których - wychodząc od stanu: wszystkie wierzchołki białe - można dojść do stanu: dokładnie jeden wierzchołek czarny.
dla których - wychodząc od stanu: wszystkie wierzchołki białe - można dojść do stanu: dokładnie jeden wierzchołek czarny.

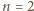 wskazany cel da się osiągnąć. W trzech ruchach wybieramy proste zawierające boki dużego trójkąta. Jego wierzchołki pozostaną białe (każdy zmieni kolor dwukrotnie), zaś środki boków staną się czarne. Teraz w jednym ruchu zmieniamy kolor dwóch z tych środków z powrotem na biały. Pozostaje jeden punkt czarny.
wskazany cel da się osiągnąć. W trzech ruchach wybieramy proste zawierające boki dużego trójkąta. Jego wierzchołki pozostaną białe (każdy zmieni kolor dwukrotnie), zaś środki boków staną się czarne. Teraz w jednym ruchu zmieniamy kolor dwóch z tych środków z powrotem na biały. Pozostaje jeden punkt czarny.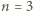 można uzyskać wymagany stan. Jak poprzednio, w trzech ruchach bierzemy proste, zawierające boki dużego trójkąta. Jego wierzchołki i jego środek staną się białe, pozostałe punkty siatki staną się czarne. W kolejnych trzech ruchach bierzemy proste równoległe do boków dużego trójkąta i przechodzące przez jego środek. Czarne punkty wybielą się, a punkt w środku się zaczerni.
można uzyskać wymagany stan. Jak poprzednio, w trzech ruchach bierzemy proste, zawierające boki dużego trójkąta. Jego wierzchołki i jego środek staną się białe, pozostałe punkty siatki staną się czarne. W kolejnych trzech ruchach bierzemy proste równoległe do boków dużego trójkąta i przechodzące przez jego środek. Czarne punkty wybielą się, a punkt w środku się zaczerni.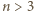 nie da się! W trójce punktów, będących wierzchołkami dużego trójkąta, po każdym ruchu jest parzysta liczba czarnych punktów (0 lub 2). Żaden z tej trójki nie może więc być owym punktem, który w pewnym momencie miałby stać się jedynym czarnym.
nie da się! W trójce punktów, będących wierzchołkami dużego trójkąta, po każdym ruchu jest parzysta liczba czarnych punktów (0 lub 2). Żaden z tej trójki nie może więc być owym punktem, który w pewnym momencie miałby stać się jedynym czarnym.