Składanie inwersji z symetrią
Inwersja jest bardzo pożytecznym przekształceniem, które ma szerokie zastosowanie w zadaniach związanych z okręgami. W wielu z nich opłaca się stosować ją w taki sposób, aby nie mnożyć punktów - innymi słowy tak dobrać promień inwersji, aby obrazy interesujących nas punktów wypadały w innych punktach rozważanej konfiguracji. Zdarza się jednak, że do uzyskania tego efektu potrzebujemy dodatkowo złożyć inwersję z symetrią.
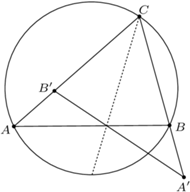
Rys. 1
Rozważmy mianowicie trójkąt 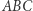 wpisany w okrąg
wpisany w okrąg 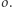 Jeśli zastosujemy inwersję o środku w punkcie
Jeśli zastosujemy inwersję o środku w punkcie 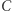 (i przez
(i przez 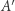 i
i 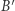 oznaczymy obrazy, odpowiednio, punktów
oznaczymy obrazy, odpowiednio, punktów 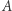 i
i 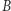 ), to otrzymamy trójkąt
), to otrzymamy trójkąt 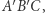 który będzie podobny do trójkąta
który będzie podobny do trójkąta 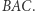 Jeśli promień inwersji będzie równy
Jeśli promień inwersji będzie równy 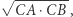 to trójkąt
to trójkąt 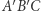 będzie przystający do trójkąta
będzie przystający do trójkąta 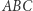 (Rys. 1). Znacznie lepszym podejściem jest rozważenie złożenia inwersji o środku
(Rys. 1). Znacznie lepszym podejściem jest rozważenie złożenia inwersji o środku 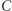 i promieniu
i promieniu 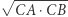 z symetrią względem dwusiecznej kąta
z symetrią względem dwusiecznej kąta 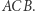 Przekształcenie to, podobnie jak inwersja, jest inwolucją, czyli złożone same z sobą daje identyczność. W takim razie zamienia ono każdy obiekt z jego obrazem. W szczególności przekształcenie to zamienia punkty
Przekształcenie to, podobnie jak inwersja, jest inwolucją, czyli złożone same z sobą daje identyczność. W takim razie zamienia ono każdy obiekt z jego obrazem. W szczególności przekształcenie to zamienia punkty 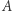 i
i 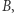 półproste
półproste 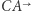 i
i 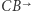 oraz wymienia prostą
oraz wymienia prostą 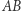 z okręgiem opisanym na trójkącie
z okręgiem opisanym na trójkącie 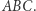 Ponadto posiada ono wszystkie własności inwersji - np. zachowuje kąty. Przekonajmy się o jego przydatności na kilku przykładach.
Ponadto posiada ono wszystkie własności inwersji - np. zachowuje kąty. Przekonajmy się o jego przydatności na kilku przykładach.
Oprócz składania inwersji z symetrią osiową możemy także złożyć inwersję z symetrią środkową (o środku w środku inwersji). Zobaczmy to na poniższym przykładzie.
Na koniec artykułu zostawiamy kilka zadań dla Czytelników.