Kącik początkującego olimpijczyka

Potęga punktu względem okręgu

Przedstawiamy wygodne narzędzie geometryczne o wielu zastosowaniach, wśród których znajduje się dowodzenie współliniowości punktów.

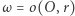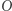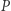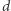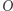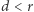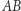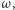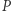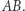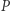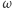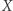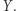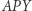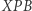Rozważmy okrąg $ω = o(O, r)$ o środku $O$ i promieniu $r$ oraz ustalmy pewien punkt $|P$ w odległości $d$ od punktu $O$ (na rysunku obok $|d < r$ ). Niech $AB$ będzie taką średnicą okręgu $ω ,$ by punkt $P$ leżał na prostej $AB.$ Przez punkt $|P$ prowadzimy dowolną prostą, która przecina okrąg $|ω$ w punktach $X$ i $Y .$ Z podobieństwa trójkątów $|APY$ i $XPB$ wynika, że

P X ⋅ PY = PA ⋅ PB = (r− d)(r + d) = r2− d2,

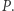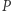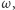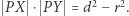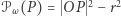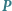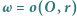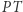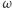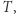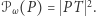
zatem wartość tego iloczynu nie zależy od wyboru prostej przechodzącej przez punkt $P.$ Pozostawiamy Czytelnikowi wykazanie, że jeśli punkt $|P$ leży na zewnątrz lub na okręgu $ω ,$ to $PX ⋅ PY = d2 − r2.$ Liczbę $2 2 |𝒫ω(P ) = OP −r$ nazywamy potęgą punktu $P$ względem okręgu $=oO,r|ω$ . Z twierdzenia Pitagorasa wynika, że jeśli prosta $|PT$ jest styczna do okręgu $|ω$ w punkcie $T ,$ to $𝒫 ω(P) = PT 2.$

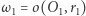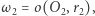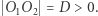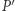Teraz rozważmy okręgi $ω 1 = o(O1, r1)$ i $ω 2 = o(O2, r2),$ dla których $| O1O2 = D > 0.$ Niech $P′$ będzie rzutem prostokątnym punktu 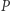$P$ na prostą 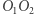$|O O 1 2$ oraz niech 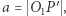$|a = O P ′ , 1$ przy czym wartość 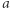$|a$ bierzemy ze znakiem minus, jeśli punkt 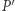$′ |P$ leży "na lewo" od 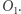$|O1.$ Po prostych rachunkach otrzymamy

2 2 2 𝒫 (P ) = 𝒫 (P ) a = r1-−r2-+D- . ω ω 2D 1 2

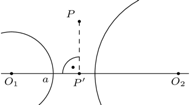
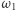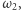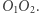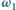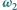To oznacza, że zbiór tych punktów, które mają jednakową potęgę względem okręgów $ω 1$ i $ω 2,$ jest prostą prostopadłą do $O1O2.$ Nazywamy ją osią potęgową okręgów $1 ω$ i $2 ω$ i będziemy oznaczać symbolem 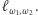$|ℓω . 1,ω 2$ Zauważmy też, że jeśli okręgi przecinają się w dwóch punktach, to ich oś potęgowa przechodzi przez te dwa punkty.

Osie potęgowe są przydatne w dowodzeniu współliniowości punktów: jeśli 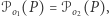$|𝒫 (P ) = 𝒫 (P ), o1 o2$ to punkt 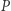$P$ leży na prostej $|ℓ . o1,o2$