W świecie liczb rzeczywistych z nierównością 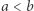niewiele da się zrobić, natomiast jeśl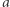i i 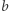są liczbami całkowitymi, to możemy ją wzmocnić: 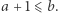W zadaniach 1, 2 i 3 korzystamy z tej własności liczb całkowitych. Nie jest to obserwacja szczególnie głęboka, ale wartościowa dzięki swym licznym zastosowaniom, przeformułowaniom i uogólnieniom. Możemy, dla przykładu, powiedzieć, że pomiędzy dwiema kolejnymi liczbami całkowitymi nie ma żadnej innej liczby całkowitej, a pomiędzy kwadratami liczb naturalnych nie ma żadnych kwadratów liczb naturalnych; analogicznie dla liczb pierwszych czy wielokrotności ustalonej liczby - w ogólności dla dowolnego ciągu rosnącego. Takie spostrzeżenia są użyteczne w zadaniach 4, 5 i 6.

Można stosować jeszcze nieco inne podejście: w każdym ograniczonym przedziale znajduje się tylko skończenie wiele liczb całkowitych. Jeżeli więc uda się jakąś niewiadomą z zadania oszacować z góry i z dołu, to możemy uwzględnić wszystkie jej możliwe wartości, rozpatrując kilka przypadków. Takie postępowanie stosujemy w zadaniach 7 i 8.

Użyteczny bywa również następujący wniosek: jeśli w pewnym zbiorze znajdziemy 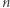różnych liczb naturalnych, to co najmniej jedna z nich jest większa lub równa 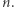Ten motyw występuje w zadaniach 9 i 10.