Kącik początkującego olimpijczyka
Trójmian kwadratowy
O stosowaniu podstawowej wiedzy szkolnej na temat funkcji kwadratowej do rozwiązywania zadań olimpijskich.
Ustalmy liczby rzeczywiste 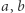 i
i 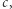 przy czym
przy czym 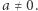 Wyrażenie
Wyrażenie 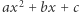 nazywamy trójmianem kwadratowym zmiennej
nazywamy trójmianem kwadratowym zmiennej 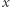 o współczynnikach
o współczynnikach 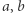 i
i 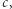 natomiast funkcję
natomiast funkcję 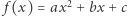 - funkcją kwadratową.
- funkcją kwadratową.
Trójmian kwadratowy można zapisać następująco:
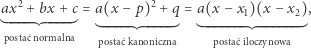
gdzie 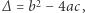
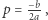
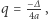
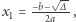
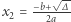 (o ile
(o ile 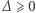 ). Dowód, który polega na zwykłym przemnażaniu, wspaniałomyślnie pomijamy.
). Dowód, który polega na zwykłym przemnażaniu, wspaniałomyślnie pomijamy.
Każda z powyższych postaci ma swoje unikalne zastosowania. Postać kanoniczna mówi nam, że funkcja kwadratowa przyjmuje wartość najmniejszą (gdy 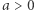 ) lub największą (gdy
) lub największą (gdy 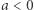 ) równą
) równą 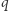 dla argumentu
dla argumentu 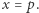 Tę postać wykorzystujemy w zadaniach 2 i 4. Postać iloczynowa jest pomocna w zadaniu 10.
Tę postać wykorzystujemy w zadaniach 2 i 4. Postać iloczynowa jest pomocna w zadaniu 10.
Wyżej określone liczby 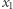 i
i 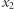 nazywamy pierwiastkami trójmianu kwadratowego
nazywamy pierwiastkami trójmianu kwadratowego 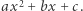 Są to miejsca zerowe funkcji kwadratowej
Są to miejsca zerowe funkcji kwadratowej 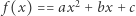 - jest jasne (postać iloczynowa), że
- jest jasne (postać iloczynowa), że 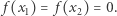 Jeśli
Jeśli 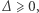 to trójmian ma dwa różne pierwiastki rzeczywiste. Jeśli
to trójmian ma dwa różne pierwiastki rzeczywiste. Jeśli 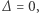 to jeden
to jeden 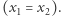 Jeśli
Jeśli 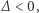 to trójmian nie ma pierwiastków rzeczywistych.
to trójmian nie ma pierwiastków rzeczywistych.
Warto jeszcze wspomnieć, że funkcja kwadratowa jest ciągła, więc ma własność Darboux - jeżeli 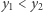 są wartościami pewnej funkcji kwadratowej, to wszystkie liczby rzeczywiste z przedziału
są wartościami pewnej funkcji kwadratowej, to wszystkie liczby rzeczywiste z przedziału ![|[y1,y2]](/math/temat/matematyka/algebra/2019/09/30/Trojmian_kwadratowy/2x-9cee0551249ea2c3ee5231f48020de33743ec8a7-im-33,33,33-FF,FF,FF.gif) też są jej wartościami. Korzystamy z tego w zadaniach 3 i 9.
też są jej wartościami. Korzystamy z tego w zadaniach 3 i 9.
Porównując postać iloczynową i normalną, otrzymamy 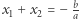 i
i 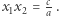 Są to wzory Viete'a, którymi warto się posłużyć w zadaniach 1, 5 i 7.
Są to wzory Viete'a, którymi warto się posłużyć w zadaniach 1, 5 i 7.