Zadania z indywidualnością
Matematyka, zwłaszcza tzw. szkolna, wypracowała przez lata procedury rozwiązywania określonego typu zadań. Gdy rozpoznajemy problem jako równanie kwadratowe, w głowie pojawia się hasło "bekwadratminusczteryace" i już wszystko wiadomo, niezależnie od tego, jak w rzeczywistości nazwaliśmy współczynniki funkcji kwadratowej...

Kiedy widzimy wartość bezwzględną wyrażenia, w pierwszym odruchu rozbijamy zadanie na przypadki: gdy wyrażenie jest dodatnie i gdy jest ujemne. Pierwiastek kwadratowy w równaniu skłania do podniesienia obu stron do kwadratu, by jak najszybciej się owego pierwiastka pozbyć. A przecież wiele zadań ma specyficzną konstrukcję, własną indywidualność, która często pozwala stosować prostsze lub bardziej eleganckie metody rozwiązania. Czyż do rozwiązania równania 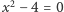 trzeba się odwoływać do wyróżnika funkcji kwadratowej?
trzeba się odwoływać do wyróżnika funkcji kwadratowej?
Nie zawsze warto poddawać się pierwszym odruchom. Rozwiązanie omijające ogólną procedurę, wykorzystujące szczególne cechy konkretnej sytuacji matematycznej, daje satysfakcję nie tylko autorowi, ale także czytelnikom tego rozwiązania, otwiera umysły i zachęca do poszukiwania własnych dróg. Nawet jeśli nietypowe rozwiązanie nie jest krótsze od rozwiązania wynikającego z procedur, warto je pokazywać. Poniżej parę przykładów rozwiązań standardowych (przez co będziemy rozumieli rozwiązania "pierwszego odruchu") i niestandardowych (wynikających z niepoddania się odruchom). Klasyfikacja rozwiązań do jednej lub drugiej kategorii jest, rzecz jasna, subiektywna - różni ludzie miewają różne odruchy - ale ułatwia ujawnienie tego, co określiliśmy jako indywidualność zadania. Niemal wszystkie przykłady, zarówno standardowe, jak i niestandardowe, pochodzą z rzeczywistych prac uczniów licealnych.
Na koniec przykład niestandardowego dowodu, który nie pochodzi z prac uczniowskich (można go odnaleźć w sieci), ale ma pewną cechę, z powodu której warto go przytoczyć. To dowód faktu, że
Na koniec przykład niestandardowego dowodu, który nie pochodzi z prac uczniowskich (można go odnaleźć w sieci), ale ma pewną cechę, z powodu której warto go przytoczyć. To dowód faktu, że
Fakt. Dla każdej liczby naturalnej 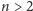 liczba
liczba 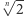 jest liczbą niewymierną.
jest liczbą niewymierną.
Dowód. Przypuśćmy, że 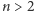 i istnieją liczby całkowite
i istnieją liczby całkowite  i
i 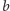 względnie pierwsze takie, że
względnie pierwsze takie, że 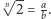 Wtedy
Wtedy 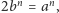 czyli
czyli 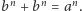 A to stoi w jawnej sprzeczności z Wielkim Twierdzeniem Fermata: dla
A to stoi w jawnej sprzeczności z Wielkim Twierdzeniem Fermata: dla 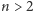 równanie
równanie 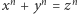 nie ma rozwiązań w liczbach całkowitych!
nie ma rozwiązań w liczbach całkowitych!
Jakaż to cecha powoduje, że warto zobaczyć ten dowód? Trudno go określić jako prostszy od dowodu standardowego, opierającego się na własnościach podzielności, gdyż zawiera potężne narzędzie, zbudowane przez Pierre'a de Fermata i Andrew Wilesa, daleko wykraczające poza to, co moglibyśmy nazwać prawem dowodu do obrony własnej. Z tego samego powodu trudno też uznać go za elegancki. Otóż jest on po prostu... zabawny!
W matematyce zdanie staje się twierdzeniem, gdy zostaje wsparte dowodem. Nierzadkie są jednak przypadki, gdy po udowodnieniu twierdzenia zaczynają pojawiać się publikacje proponujące inny jego dowód. Dlaczego dowodzi się czegoś, co już zostało udowodnione? Po pierwsze dlatego, że nieustannie trwa poszukiwanie dowodów prostych i ładnych. Po drugie zaś dlatego, że nowy dowód często odwołuje się do zupełnie innych własności matematycznych niż poprzednie, co pozwala zobaczyć samo twierdzenie pod innym kątem i lepiej zrozumieć jego miejsce wśród innych. Co widać na podanych wyżej prostych przykładach.