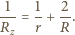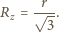Wprowadźmy układ współrzędnych o początku w jednym z wierzchołków podstawy akwarium, na przecięciu poziomej osi 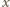 równoległej do
równoległej do 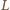 oraz osi
oraz osi 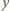 skierowanej pionowo w górę. Środek ciężkości wody przez cały czas ruchu pozostaje w jednakowej odległości od pionowych ścian akwarium równoległych do płaszczyzny
skierowanej pionowo w górę. Środek ciężkości wody przez cały czas ruchu pozostaje w jednakowej odległości od pionowych ścian akwarium równoległych do płaszczyzny 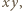 a okres badanych drgań nie zależy od szerokości naczynia. Podczas drgań, gdy na bocznej ściance o współrzędnej
a okres badanych drgań nie zależy od szerokości naczynia. Podczas drgań, gdy na bocznej ściance o współrzędnej 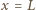 woda podnosi się na wysokość
woda podnosi się na wysokość 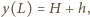 to na ściance
to na ściance 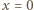 opada do
opada do 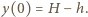 Środek ciężkości wody przesuwa się wówczas z położenia równowagi
Środek ciężkości wody przesuwa się wówczas z położenia równowagi 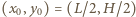 w położenie:
w położenie:
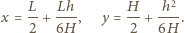
Dla małych drgań przyjmujemy, że 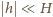 oraz
oraz 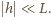 Wyprowadzając powyższe wyrażenia, skorzystaliśmy z faktu, że dla każdego
Wyprowadzając powyższe wyrażenia, skorzystaliśmy z faktu, że dla każdego 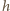 rozkład wody w naczyniu możemy otrzymać, dodając do rozkładu równowagowego wodę wypełniającą prostopadłościan o podstawie trójkąta prostokątnego z poziomą przyprostokątną
rozkład wody w naczyniu możemy otrzymać, dodając do rozkładu równowagowego wodę wypełniającą prostopadłościan o podstawie trójkąta prostokątnego z poziomą przyprostokątną 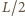 i pionową
i pionową 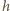 - po stronie
- po stronie 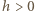 i odejmując taki sam prostopadłościan po stronie
i odejmując taki sam prostopadłościan po stronie 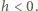 Pamiętamy też, że środek ciężkości jednorodnego trójkąta leży na przecięciu środkowych jego boków - dla trójkąta prostokątnego rzuty prostokątne środka ciężkości wypadają w 1/3 odpowiednich przyprostokątnych, licząc od wierzchołka kąta prostego. Kwadrat prędkości ruchu środka masy wynosi więc:
Pamiętamy też, że środek ciężkości jednorodnego trójkąta leży na przecięciu środkowych jego boków - dla trójkąta prostokątnego rzuty prostokątne środka ciężkości wypadają w 1/3 odpowiednich przyprostokątnych, licząc od wierzchołka kąta prostego. Kwadrat prędkości ruchu środka masy wynosi więc:
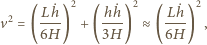
gdzie 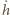 oznacza pochodną
oznacza pochodną 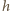 względem czasu. Jako kolejne przybliżenie przyjmijmy, że cała masa
względem czasu. Jako kolejne przybliżenie przyjmijmy, że cała masa 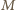 wody porusza się z tą sama prędkością
wody porusza się z tą sama prędkością 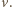 Wówczas zmiany całkowitej energii mechanicznej
Wówczas zmiany całkowitej energii mechanicznej 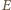 podczas ruchu możemy zapisać jako:
podczas ruchu możemy zapisać jako:
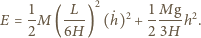
Wyrażenie to "przypomina" nam wzór na energię drgań masy  zawieszonej na sprężynie o stałej sprężystości
zawieszonej na sprężynie o stałej sprężystości 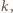 jeśli przyjmiemy:
jeśli przyjmiemy:
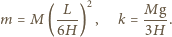
Poszukiwany okres drgań wynosi więc:
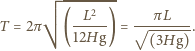
W akwarium o 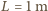 i
i 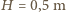
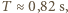 natomiast, na przykład, dla Jeziora Genewskiego, dla którego można przyjąć
natomiast, na przykład, dla Jeziora Genewskiego, dla którego można przyjąć 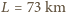 i średnią głębokość
i średnią głębokość 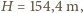 obliczone
obliczone 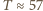 minut (obserwowano fale o
minut (obserwowano fale o 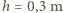 i
i 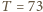 minuty).
minuty).

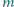 i stałej dielektrycznej
i stałej dielektrycznej 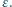 Okładki kondensatora mają rozmiary
Okładki kondensatora mają rozmiary 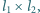 odległość między nimi wynosi
odległość między nimi wynosi 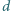 (
( 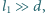
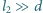 ). Między okładkami utrzymywane jest stałe napięcie
). Między okładkami utrzymywane jest stałe napięcie 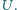 Płytkę wysunięto z obszaru kondensatora wzdłuż boku o długości
Płytkę wysunięto z obszaru kondensatora wzdłuż boku o długości 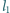 na odległość
na odległość 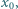 a następnie puszczono swobodnie. Zaniedbując tarcie, znaleźć zależność przemieszczenia i prędkości płytki od czasu.
a następnie puszczono swobodnie. Zaniedbując tarcie, znaleźć zależność przemieszczenia i prędkości płytki od czasu.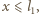 pojemność kondensatora wynosi
pojemność kondensatora wynosi ![c(x) = є0l2[x + є(l1− x)]/d,](/math/temat/fizyka/e_i_m/zadania/2016/05/01/zf-k44-619/2x-2e05e6822c69487536beed78f814b0b27b4b8119-im-66,57,43-FF,FF,FF.gif) energia
energia 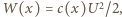 ładunek na okładkach
ładunek na okładkach 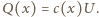 Oznaczając przez
Oznaczając przez 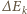 zmianę energii kinetycznej kondensatora, gdy położenie płytki zmienia się o
zmianę energii kinetycznej kondensatora, gdy położenie płytki zmienia się o 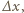 możemy napisać bilans energii:
możemy napisać bilans energii: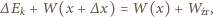
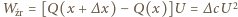 jest pracą źródła. Stąd
jest pracą źródła. Stąd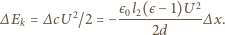


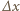 jest małe, możemy przyjąć, że siła
jest małe, możemy przyjąć, że siła 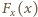 działająca na dielektryk wzdłuż osi
działająca na dielektryk wzdłuż osi 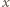 nie zmienia się, zatem
nie zmienia się, zatem 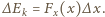 Dla dodatnich
Dla dodatnich 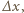 energia kinetyczna maleje, dielektryk jest więc wciągany do kondensatora siłą o stałej wartości
energia kinetyczna maleje, dielektryk jest więc wciągany do kondensatora siłą o stałej wartości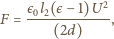
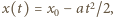 prędkość
prędkość 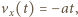 gdzie
gdzie 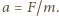 Dielektryk wykonuje więc drgania wokół położenia równowagi dla
Dielektryk wykonuje więc drgania wokół położenia równowagi dla 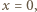 gdzie prędkość osiąga maksymalną wartość
gdzie prędkość osiąga maksymalną wartość 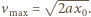 Okres drgań wynosi
Okres drgań wynosi 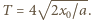 Zależność położenia i prędkości dielektryka od czasu przedstawiona jest na wykresach (rysunki 1 i 2), wykres położenia składa się z fragmentów parabol.
Zależność położenia i prędkości dielektryka od czasu przedstawiona jest na wykresach (rysunki 1 i 2), wykres położenia składa się z fragmentów parabol. pod kątem
pod kątem  do poziomu. Po narysowanej krzywej pełznie mały żuczek, którego prędkość ma stałą wartość
do poziomu. Po narysowanej krzywej pełznie mały żuczek, którego prędkość ma stałą wartość  Ile wynosi przyspieszenie żuczka w punkcie odpowiadającym maksymalnej wysokości, na jaką wzniósł się kamień. Oporu powietrza podczas ruchu kamienia nie uwzględniamy.
Ile wynosi przyspieszenie żuczka w punkcie odpowiadającym maksymalnej wysokości, na jaką wzniósł się kamień. Oporu powietrza podczas ruchu kamienia nie uwzględniamy.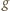 jest prostopadłe do toru i jest przyspieszeniem dośrodkowym:
jest prostopadłe do toru i jest przyspieszeniem dośrodkowym: 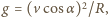 gdzie
gdzie 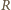 jest promieniem krzywizny toru w rozważanym punkcie. Promień krzywizny toru w odpowiadającym punkcie na rysunku wynosi
jest promieniem krzywizny toru w rozważanym punkcie. Promień krzywizny toru w odpowiadającym punkcie na rysunku wynosi 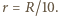 Przyspieszenie żuczka jest prostopadłe do toru (bo jego wartość prędkości jest stała) i wynosi
Przyspieszenie żuczka jest prostopadłe do toru (bo jego wartość prędkości jest stała) i wynosi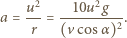
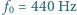 . Wartości prędkości pociągów w chwili włączenia sygnałów są równe
. Wartości prędkości pociągów w chwili włączenia sygnałów są równe 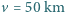 /h. Prędkość dźwięku w powietrzu wynosi
/h. Prędkość dźwięku w powietrzu wynosi 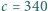 m/s. Przyjmij, że każdy z sygnałów rozprzestrzenia się jako fala harmoniczna. Jakiej częstości dźwięk usłyszy każdy z maszynistów przed spotkaniem pociągów?
m/s. Przyjmij, że każdy z sygnałów rozprzestrzenia się jako fala harmoniczna. Jakiej częstości dźwięk usłyszy każdy z maszynistów przed spotkaniem pociągów?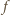 :
: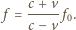
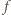 i
i 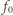 daje sygnał o częstości
daje sygnał o częstości 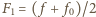 o amplitudzie modulowanej z częstością
o amplitudzie modulowanej z częstością 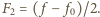 Podstawiając dane, otrzymujemy:
Podstawiając dane, otrzymujemy: 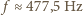 ,
, 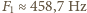 i
i 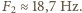
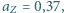 a od Księżyca
a od Księżyca 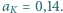 Odległość Ziemia-Słońce
Odległość Ziemia-Słońce 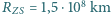 , odległość Ziemia-Księżyc
, odległość Ziemia-Księżyc 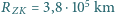 , promień Ziemi
, promień Ziemi 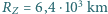 , promień Księżyca
, promień Księżyca 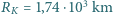 .
.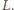 W odległości
W odległości 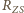 od Słońca na jednostkę powierzchni pada moc
od Słońca na jednostkę powierzchni pada moc 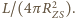 Oświetlona w tej odległości powierzchnia kuli o promieniu
Oświetlona w tej odległości powierzchnia kuli o promieniu 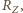 współczynniku odbicia
współczynniku odbicia 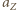 staje się wtórnym źródłem wysyłającym promieniowanie o mocy
staje się wtórnym źródłem wysyłającym promieniowanie o mocy 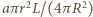 w kąt bryłowy
w kąt bryłowy 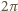 (oświetlona jest półkula), a więc w odległości równej odległości Księżyca od Ziemi przypadająca na jednostkę powierzchni moc światła odbitego od Ziemi,
(oświetlona jest półkula), a więc w odległości równej odległości Księżyca od Ziemi przypadająca na jednostkę powierzchni moc światła odbitego od Ziemi, 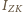 wynosi:
wynosi: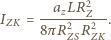
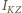 należy zastąpić
należy zastąpić 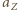 przez
przez 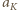 i
i 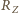 przez
przez 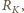 a
a 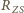 przez sumę odległości Ziemia-Słońce i Ziemia-Księżyc (podczas pełni Księżyc jest po przeciwnej stronie Ziemi niż Słońce),
przez sumę odległości Ziemia-Słońce i Ziemia-Księżyc (podczas pełni Księżyc jest po przeciwnej stronie Ziemi niż Słońce), 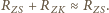 Ostatnie przybliżenie uwzględnia niewielką odległość Ziemia-Księżyc w porównaniu z odległością Ziemia-Słońce. Po podstawieniu odpowiednich wartości otrzymujemy:
Ostatnie przybliżenie uwzględnia niewielką odległość Ziemia-Księżyc w porównaniu z odległością Ziemia-Słońce. Po podstawieniu odpowiednich wartości otrzymujemy: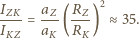
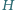 na nieruchomą rakietkę odbija się na wysokość
na nieruchomą rakietkę odbija się na wysokość 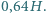 Chłopiec podbija periodycznie taką piłeczkę pionowo do góry tak, że po każdym uderzeniu wznosi się ona na wysokość
Chłopiec podbija periodycznie taką piłeczkę pionowo do góry tak, że po każdym uderzeniu wznosi się ona na wysokość 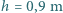 powyżej rakietki. Z jaką prędkością rakietka porusza się ku górze w momencie uderzenia? Przyjmujemy, że masa rakietki jest dużo większa od masy piłeczki.
powyżej rakietki. Z jaką prędkością rakietka porusza się ku górze w momencie uderzenia? Przyjmujemy, że masa rakietki jest dużo większa od masy piłeczki.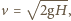 gdzie
gdzie 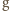 to przyspieszenie ziemskie. Po odbiciu piłeczka uzyskuje prędkość
to przyspieszenie ziemskie. Po odbiciu piłeczka uzyskuje prędkość 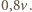 Niech teraz rakietka w momencie odbicia piłeczki porusza się ku górze z prędkością
Niech teraz rakietka w momencie odbicia piłeczki porusza się ku górze z prędkością 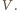 W układzie współrzędnych, związanym z rakietką, piłeczka ma w momencie zderzenia prędkość
W układzie współrzędnych, związanym z rakietką, piłeczka ma w momencie zderzenia prędkość 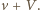 Po zderzeniu jej prędkość w tym układzie odniesienia wyniesie
Po zderzeniu jej prędkość w tym układzie odniesienia wyniesie 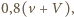 czyli w nieruchomym układzie odniesienia będzie miała prędkość
czyli w nieruchomym układzie odniesienia będzie miała prędkość 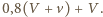 Ponieważ po podbiciu piłeczka ma się wznieść na taką wysokość, z jakiej spadła, to musi być spełniona zależność
Ponieważ po podbiciu piłeczka ma się wznieść na taką wysokość, z jakiej spadła, to musi być spełniona zależność 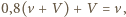 a stąd
a stąd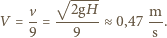
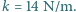 Ile wynosi współczynnik sprężystości drugiej sprężyny?
Ile wynosi współczynnik sprężystości drugiej sprężyny?![|k [N/m] = Ca](/math/temat/fizyka/materialy/zadania/2016/03/27/zf-901/1x-f7ad50941f84147361991616a21cf5c5961bad50-im-66,57,43-FF,FF,FF.gif) gdzie
gdzie 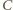 - stała bezwymiarowa,
- stała bezwymiarowa, 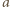 - któryś z geometrycznych rozmiarów sprężyny,
- któryś z geometrycznych rozmiarów sprężyny, 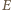 - moduł Younga. Wyobraźmy sobie trzecią sprężynę o średnicy
- moduł Younga. Wyobraźmy sobie trzecią sprężynę o średnicy 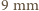 i długości
i długości 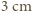 wykonaną z drutu o średnicy
wykonaną z drutu o średnicy 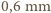 . Miałaby ona współczynnik sprężystości trzy razy większy od sprężyny pierwszej, to znaczy
. Miałaby ona współczynnik sprężystości trzy razy większy od sprężyny pierwszej, to znaczy 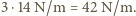 Równocześnie współczynniki sprężystości trzeciej i drugiej sprężyny pozostają w stosunku 3/7. Stąd otrzymujemy, że współczynnik sprężystości drugiej sprężyny wynosi
Równocześnie współczynniki sprężystości trzeciej i drugiej sprężyny pozostają w stosunku 3/7. Stąd otrzymujemy, że współczynnik sprężystości drugiej sprężyny wynosi 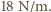
 jednakowych sprężyn, każda o współczynniku sprężystości
jednakowych sprężyn, każda o współczynniku sprężystości 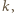 daje sprężynę o współczynniku sprężystości
daje sprężynę o współczynniku sprężystości 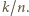 )
)
 wartość wektora indukcji pola magnetycznego rośnie liniowo w czasie:
wartość wektora indukcji pola magnetycznego rośnie liniowo w czasie: 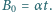 Linie pola magnetycznego są równoległe do osi walca. Jak musi zmieniać się w czasie wartość jednorodnego pola magnetycznego wewnątrz tej powierzchni, aby elektron poruszał się po okręgu o promieniu
Linie pola magnetycznego są równoległe do osi walca. Jak musi zmieniać się w czasie wartość jednorodnego pola magnetycznego wewnątrz tej powierzchni, aby elektron poruszał się po okręgu o promieniu 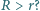 W chwili
W chwili 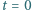 elektron spoczywa.
elektron spoczywa.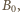 ponieważ wewnątrz powierzchni walcowej nie płynie żaden prąd. Jeżeli elektron porusza się po okręgu o promieniu
ponieważ wewnątrz powierzchni walcowej nie płynie żaden prąd. Jeżeli elektron porusza się po okręgu o promieniu 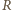 i ma w danej chwili prędkość
i ma w danej chwili prędkość 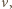 to działająca na niego siła dośrodkowa jest siłą Lorentza:
to działająca na niego siła dośrodkowa jest siłą Lorentza: 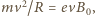 zatem jego prędkość
zatem jego prędkość 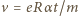 rośnie liniowo w czasie. Prędkość tę uzyskuje elektron dzięki sile elektrycznej
rośnie liniowo w czasie. Prędkość tę uzyskuje elektron dzięki sile elektrycznej 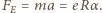 Wektor natężenia pola elektrycznego o długości
Wektor natężenia pola elektrycznego o długości 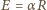 jest styczny do okręgu. Z prawa Maxwella wiemy, że krążenie pola elektrycznego wzdłuż okręgu o promieniu
jest styczny do okręgu. Z prawa Maxwella wiemy, że krążenie pola elektrycznego wzdłuż okręgu o promieniu 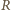 ma wartość bezwzględną
ma wartość bezwzględną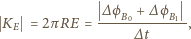
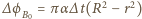 jest zmianą w czasie
jest zmianą w czasie 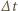 strumienia pola
strumienia pola 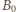 przez powierzchnię objętą okręgiem,
przez powierzchnię objętą okręgiem, 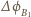 jest zmianą strumienia szukanego pola
jest zmianą strumienia szukanego pola 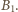 Ponieważ
Ponieważ 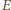 nie zależy od czasu,
nie zależy od czasu, 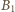 musi być liniową funkcją czasu:
musi być liniową funkcją czasu: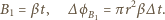
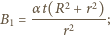
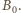

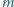 połączonych nieważką sprężyną o współczynniku sprężystości
połączonych nieważką sprężyną o współczynniku sprężystości 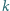 znajduje się w stanie równowagi. Górną płytkę naciśnięto tak, że opuściła się ona o
znajduje się w stanie równowagi. Górną płytkę naciśnięto tak, że opuściła się ona o 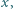 a następnie puszczono. Na jaką maksymalną wysokość podniósł się środek masy układu?
a następnie puszczono. Na jaką maksymalną wysokość podniósł się środek masy układu?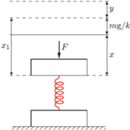
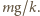 Dolna płytka oderwie się od podłoża, gdy siła
Dolna płytka oderwie się od podłoża, gdy siła 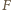 powodująca dodatkowe ściśnięcie sprężyny o
powodująca dodatkowe ściśnięcie sprężyny o 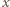 będzie większa od ciężaru układu, czyli spełniony będzie warunek
będzie większa od ciężaru układu, czyli spełniony będzie warunek 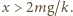 W chwili oderwania sprężyna będzie wydłużona o
W chwili oderwania sprężyna będzie wydłużona o 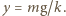 Prędkość
Prędkość  górnej płytki w chwili oderwania dolnej znajdujemy z zasady zachowania energii:
górnej płytki w chwili oderwania dolnej znajdujemy z zasady zachowania energii: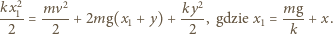
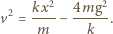
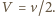 Po oderwaniu środek masy porusza się ruchem jednostajnie opóźnionym i wznosi się na wysokość
Po oderwaniu środek masy porusza się ruchem jednostajnie opóźnionym i wznosi się na wysokość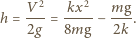
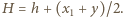 Jeśli
Jeśli 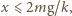 dolna płytka pozostaje w spoczynku, a górna porusza się ruchem harmonicznym wokół położenia równowagi z amplitudą
dolna płytka pozostaje w spoczynku, a górna porusza się ruchem harmonicznym wokół położenia równowagi z amplitudą 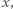 czyli wznosi się na maksymalną wysokość
czyli wznosi się na maksymalną wysokość 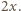 Zatem odpowiedź na postawione pytanie jest następująca: maksymalna wysokość, na jaką wzniesie się środek masy układu, dana jest wzorem:
Zatem odpowiedź na postawione pytanie jest następująca: maksymalna wysokość, na jaką wzniesie się środek masy układu, dana jest wzorem: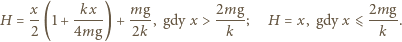
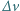 prędkości molekuł w wiązce, jeśli chcemy zaobserwować wyraźne prążki do rzędu
prędkości molekuł w wiązce, jeśli chcemy zaobserwować wyraźne prążki do rzędu 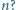 Rozrzut
Rozrzut 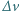 prędkości
prędkości  w wiązce o średniej prędkości
w wiązce o średniej prędkości 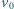 określają nierówności
określają nierówności 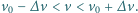
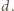 Wówczas kolejne prążki interferencyjne pojawią się pod kątami
Wówczas kolejne prążki interferencyjne pojawią się pod kątami 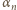 spełniającymi warunek
spełniającymi warunek 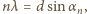 gdzie
gdzie 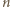 jest rzędem prążka,
jest rzędem prążka, 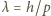 długością fali de Broglie'a,
długością fali de Broglie'a, 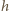 jest stałą Plancka, a
jest stałą Plancka, a 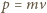 pędem molekuły o masie
pędem molekuły o masie  Rozrzut prędkości prowadzi do poszerzenia prążków. Obserwacja prążków rzędu
Rozrzut prędkości prowadzi do poszerzenia prążków. Obserwacja prążków rzędu 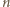 wymaga, by prążki "nie zachodziły na siebie", czyli (dla niedużych katów sinus jest funkcją rosnącą):
wymaga, by prążki "nie zachodziły na siebie", czyli (dla niedużych katów sinus jest funkcją rosnącą): 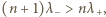 gdzie
gdzie 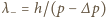 i
i 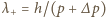 oznaczają górną i dolną granicę przedziału długości fal de Broglie'a wiązki. Ostatecznie otrzymujemy
oznaczają górną i dolną granicę przedziału długości fal de Broglie'a wiązki. Ostatecznie otrzymujemy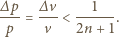
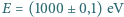 - tzn. pomiar wykonano z dokładnością do
- tzn. pomiar wykonano z dokładnością do 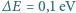 . Wyznacz stosunek dokładności określenia położenia (współrzędnej
. Wyznacz stosunek dokładności określenia położenia (współrzędnej  w kierunku ruchu) elektronu do długości jego fali de Broglie'a bezpośrednio po tym pomiarze.
w kierunku ruchu) elektronu do długości jego fali de Broglie'a bezpośrednio po tym pomiarze.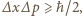 gdzie
gdzie 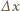 i
i 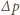 to odpowiednio dokładność pomiaru współrzędnej
to odpowiednio dokładność pomiaru współrzędnej 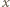 i pędu
i pędu 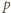 w kierunku
w kierunku 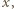 a
a 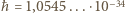 Js jest stałą Plancka
Js jest stałą Plancka 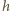 podzieloną przez
podzieloną przez 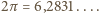
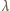 fali de Broglie'a cząstki o pędzie
fali de Broglie'a cząstki o pędzie 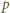 wynosi
wynosi 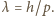 Mamy więc
Mamy więc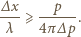
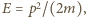 gdzie
gdzie  oznacza masę cząstki. Stąd w przybliżeniu mamy
oznacza masę cząstki. Stąd w przybliżeniu mamy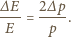

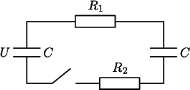
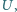 drugi nie był naładowany. Pojemności kondensatorów są jednakowe i równe
drugi nie był naładowany. Pojemności kondensatorów są jednakowe i równe 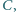 wartości oporów wynoszą
wartości oporów wynoszą 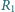 i
i 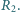
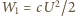 , a jego ładunek jest równy
, a jego ładunek jest równy 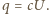 Po zamknięciu klucza napięcie na równolegle połączonych kondensatorach ma wartość
Po zamknięciu klucza napięcie na równolegle połączonych kondensatorach ma wartość 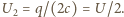 Energia układu kondensatorów wynosi
Energia układu kondensatorów wynosi 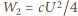 i jest mniejsza od początkowej o wielkość
i jest mniejsza od początkowej o wielkość 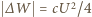 , równą całkowitemu wydzielonemu ciepłu
, równą całkowitemu wydzielonemu ciepłu 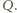 Natężenie prądu płynącego przez oba oporniki podczas przeładowywania kondensatorów jest w każdej chwili jednakowe, zatem ciepło wydzielone na oporze
Natężenie prądu płynącego przez oba oporniki podczas przeładowywania kondensatorów jest w każdej chwili jednakowe, zatem ciepło wydzielone na oporze 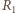 dane jest wzorem
dane jest wzorem 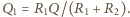 Ostatecznie
Ostatecznie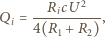
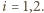
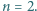 Gdy do uzwojenia pierwotnego przyłożono napięcie przemienne o amplitudzie
Gdy do uzwojenia pierwotnego przyłożono napięcie przemienne o amplitudzie 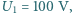 amplituda napięcia na otwartym uzwojeniu wtórnym wynosiła
amplituda napięcia na otwartym uzwojeniu wtórnym wynosiła 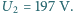 Jaka będzie amplituda napięcia na otwartym uzwojeniu wtórnym, gdy rdzeń transformatora zastąpimy rdzeniem o tych samych wymiarach, ale wykonanym z materiału o przenikalności magnetycznej
Jaka będzie amplituda napięcia na otwartym uzwojeniu wtórnym, gdy rdzeń transformatora zastąpimy rdzeniem o tych samych wymiarach, ale wykonanym z materiału o przenikalności magnetycznej 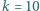 razy mniejszej niż w pierwszym przypadku? Rozpraszanie strumienia magnetycznego oraz straty w rdzeniu możemy zaniedbać.
razy mniejszej niż w pierwszym przypadku? Rozpraszanie strumienia magnetycznego oraz straty w rdzeniu możemy zaniedbać.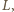 w drugim przez
w drugim przez 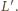 Współczynnik samoindukcji cewki jest proporcjonalny do przenikalności magnetycznej rdzenia, stąd
Współczynnik samoindukcji cewki jest proporcjonalny do przenikalności magnetycznej rdzenia, stąd 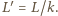 Uzwojenie możemy traktować jako połączenie szeregowe oporu czynnego
Uzwojenie możemy traktować jako połączenie szeregowe oporu czynnego 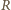 oraz indukcyjnego
oraz indukcyjnego 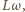 gdzie
gdzie 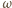 jest częstością napięcia zasilającego. Amplituda napięcia na oporze indukcyjnym wynosi
jest częstością napięcia zasilającego. Amplituda napięcia na oporze indukcyjnym wynosi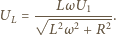
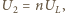 stąd
stąd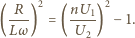
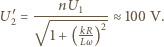
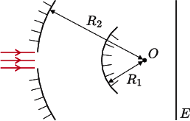
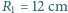 i
i 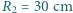 . Jaka jest ogniskowa cienkiej soczewki, za pomocą której można otrzymać obraz Słońca o takiej samej wielkości?
. Jaka jest ogniskowa cienkiej soczewki, za pomocą której można otrzymać obraz Słońca o takiej samej wielkości?
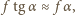 gdzie
gdzie 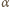 jest promieniem kątowym Słońca widzianego z Ziemi, a
jest promieniem kątowym Słońca widzianego z Ziemi, a 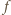 ogniskową soczewki albo zwierciadła. Obraz pozorny Słońca w zwierciadle wypukłym o ogniskowej
ogniskową soczewki albo zwierciadła. Obraz pozorny Słońca w zwierciadle wypukłym o ogniskowej 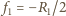 ma promień
ma promień 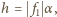 jest przedmiotem dla zwierciadła wklęsłego o ogniskowej
jest przedmiotem dla zwierciadła wklęsłego o ogniskowej 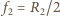 i znajduje się w odległości od niego równej
i znajduje się w odległości od niego równej 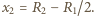 Obraz, który powstaje w zwierciadle wklęsłym, oddalony jest od niego o
Obraz, który powstaje w zwierciadle wklęsłym, oddalony jest od niego o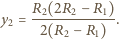
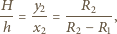
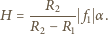
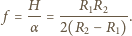

 do którego doczepiono nieważką sprężynę o współczynniku sprężystości
do którego doczepiono nieważką sprężynę o współczynniku sprężystości 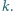 W pewnej chwili wolny koniec sprężyny zaczęto ciągnąć tak, że poruszał się on ze stałą poziomą prędkością
W pewnej chwili wolny koniec sprężyny zaczęto ciągnąć tak, że poruszał się on ze stałą poziomą prędkością  Jaką drogę przebędzie klocek do momentu, w którym osiągnie on prędkość
Jaką drogę przebędzie klocek do momentu, w którym osiągnie on prędkość 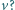 Współczynniki tarcia statycznego i kinetycznego między klockiem a podłożem wynoszą odpowiednio
Współczynniki tarcia statycznego i kinetycznego między klockiem a podłożem wynoszą odpowiednio 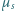 i
i 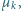 przy czym
przy czym 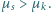
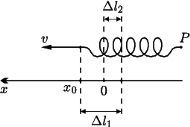
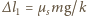 i przyjmijmy tę chwilę za początkową. W układzie odniesienia związanym ze swobodnym końcem
i przyjmijmy tę chwilę za początkową. W układzie odniesienia związanym ze swobodnym końcem 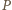 sprężyny klocek zacznie oddalać się ruchem harmonicznym od położenia równowagi (
sprężyny klocek zacznie oddalać się ruchem harmonicznym od położenia równowagi ( 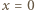 na rysunku), gdzie wydłużenie sprężyny wynosi
na rysunku), gdzie wydłużenie sprężyny wynosi 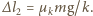 W chwili początkowej prędkość klocka wynosi
W chwili początkowej prędkość klocka wynosi 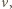 a jego odległość od położenia równowagi jest równa
a jego odległość od położenia równowagi jest równa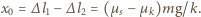
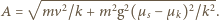
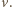 Ruch klocka do chwili, gdy oddali się na maksymalną odległość
Ruch klocka do chwili, gdy oddali się na maksymalną odległość 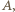 opisuje wzór
opisuje wzór 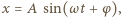 gdzie
gdzie 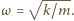 Z warunku początkowego
Z warunku początkowego 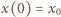 otrzymujemy przesunięcie fazowe
otrzymujemy przesunięcie fazowe 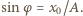 Czas
Czas 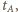 po którym odległość od położenia równowagi osiągnie wartość
po którym odległość od położenia równowagi osiągnie wartość 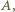 dostajemy ze wzoru
dostajemy ze wzoru 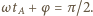 Odległość klocka od położenia początkowego w układzie związanym z końcem sprężyny równa jest
Odległość klocka od położenia początkowego w układzie związanym z końcem sprężyny równa jest 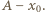 Szukana droga przebyta przez klocek w układzie związanym z podłożem wynosi
Szukana droga przebyta przez klocek w układzie związanym z podłożem wynosi 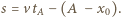

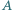 prostokątnej studni o szerokości
prostokątnej studni o szerokości 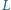 i głębokości
i głębokości 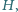 aby w wyniku odbicia od jej dna trafiła dokładnie w jej przeciwną krawędź
aby w wyniku odbicia od jej dna trafiła dokładnie w jej przeciwną krawędź 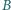 (rysunek)? Przyjąć, że ścianki i dno studni są doskonale gładkie, odbicia są doskonale sprężyste i można zaniedbać wszelkie straty energii.
(rysunek)? Przyjąć, że ścianki i dno studni są doskonale gładkie, odbicia są doskonale sprężyste i można zaniedbać wszelkie straty energii.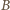 po jednym lub większej liczbie odbić od dna i towarzyszących im ewentualnie odbiciach od ścianek studni. Jeżeli nastąpiło
po jednym lub większej liczbie odbić od dna i towarzyszących im ewentualnie odbiciach od ścianek studni. Jeżeli nastąpiło 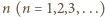 odbić od dna, to kulka znajdzie się na wysokości
odbić od dna, to kulka znajdzie się na wysokości 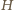 od dna studni po czasie
od dna studni po czasie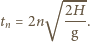
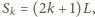 gdzie
gdzie 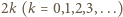 jest liczbą uderzeń kulki o pionowe ścianki studni. Stąd otrzymujemy, że prędkość kulki w punkcie
jest liczbą uderzeń kulki o pionowe ścianki studni. Stąd otrzymujemy, że prędkość kulki w punkcie 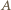 powinna być równa:
powinna być równa: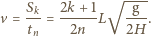
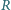 naciągnięto ciasny, gumowy pierścień. Siła rozciągająca pierścień wynosi
naciągnięto ciasny, gumowy pierścień. Siła rozciągająca pierścień wynosi 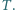 Jaką siłę trzeba przyłożyć, aby przesunąć pierścień, bez obrotu, wzdłuż osi walca? Współczynnik tarcia między stalą i gumą wynosi
Jaką siłę trzeba przyłożyć, aby przesunąć pierścień, bez obrotu, wzdłuż osi walca? Współczynnik tarcia między stalą i gumą wynosi 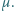 Przyjąć, że siła przesuwająca jest rozłożona równomiernie wzdłuż pierścienia.
Przyjąć, że siła przesuwająca jest rozłożona równomiernie wzdłuż pierścienia.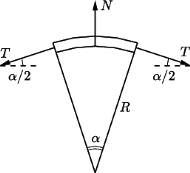
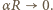 Na każdy odcinek działają siły naciągu pierścienia
Na każdy odcinek działają siły naciągu pierścienia 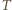 i reakcji walca
i reakcji walca 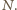 Ich suma jest równa zero, bo pierścień nie obraca się. Stąd
Ich suma jest równa zero, bo pierścień nie obraca się. Stąd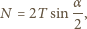
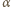 daje
daje 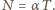 Stąd możemy obliczyć siłę tarcia, działającą na taki odcinek, przy przesuwaniu pierścienia wzdłuż walca:
Stąd możemy obliczyć siłę tarcia, działającą na taki odcinek, przy przesuwaniu pierścienia wzdłuż walca: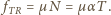
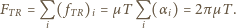
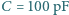 wypełniono roztworem soli kuchennej o oporze właściwym
wypełniono roztworem soli kuchennej o oporze właściwym 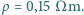 Ile wynosi opór elektryczny
Ile wynosi opór elektryczny 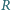 między elektrodami tak otrzymanego opornika? Przenikalność elektryczna próżni to
między elektrodami tak otrzymanego opornika? Przenikalność elektryczna próżni to 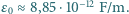
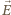 w każdym punkcie powierzchni każdej z elektrod jest do tej powierzchni prostopadły, a jego wartość jest proporcjonalna do napięcia
w każdym punkcie powierzchni każdej z elektrod jest do tej powierzchni prostopadły, a jego wartość jest proporcjonalna do napięcia 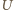 między elektrodami. Powierzchniowa gęstość ładunku w każdym punkcie elektrody kondensatora jest równa
między elektrodami. Powierzchniowa gęstość ładunku w każdym punkcie elektrody kondensatora jest równa 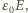 gdyż przenikalność elektryczna powietrza jest praktycznie równa przenikalności próżni. Normalna składowa gęstości prądu jest także proporcjonalna do wartości pola
gdyż przenikalność elektryczna powietrza jest praktycznie równa przenikalności próżni. Normalna składowa gęstości prądu jest także proporcjonalna do wartości pola 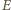 i jest równa
i jest równa 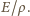 W związku z tym, przy tym samym napięciu
W związku z tym, przy tym samym napięciu 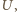 całkowity ładunek zgromadzony na powierzchni elektrod
całkowity ładunek zgromadzony na powierzchni elektrod 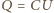 jest proporcjonalny do całkowitego prądu
jest proporcjonalny do całkowitego prądu 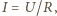 który popłynie po wypełnieniu kondensatora roztworem soli. Otrzymujemy więc:
który popłynie po wypełnieniu kondensatora roztworem soli. Otrzymujemy więc: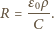
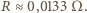
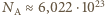 atomów. Gramoatom to liczba gramów pierwiastka równa (z bardzo dobrym przybliżeniem sumie liczb protonów i neutronów jądra atomu). Ciało człowieka zbudowane jest głównie z atomów tlenu, węgla wodoru, azotu. Poza wodorem wymienione pierwiastki występują niemal wyłącznie w postaci izotopów o równej liczbie protonów i neutronów, a więc w każdym ich gramoatomie mamy
atomów. Gramoatom to liczba gramów pierwiastka równa (z bardzo dobrym przybliżeniem sumie liczb protonów i neutronów jądra atomu). Ciało człowieka zbudowane jest głównie z atomów tlenu, węgla wodoru, azotu. Poza wodorem wymienione pierwiastki występują niemal wyłącznie w postaci izotopów o równej liczbie protonów i neutronów, a więc w każdym ich gramoatomie mamy 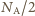 protonów. Wodór to niemal wyłącznie izotop
protonów. Wodór to niemal wyłącznie izotop 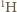 najczęściej związany w cząsteczkach wody (stanowiącej składnik żywych komórek). W cząsteczce wody mamy 10 protonów i 8 neutronów, co oznacza, że jeśli pominiemy niewielką różnicę mas protonu i neutronu, to
najczęściej związany w cząsteczkach wody (stanowiącej składnik żywych komórek). W cząsteczce wody mamy 10 protonów i 8 neutronów, co oznacza, że jeśli pominiemy niewielką różnicę mas protonu i neutronu, to 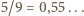 masy wody przypada na protony. Z dokładnością do
masy wody przypada na protony. Z dokładnością do 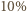 możemy więc przyjąć, że średnio 1 g naszego ciała zawiera około
możemy więc przyjąć, że średnio 1 g naszego ciała zawiera około 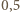 g protonów, a więc około
g protonów, a więc około 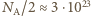 protonów i tyle samo elektronów.
protonów i tyle samo elektronów.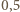 i nieznacznie maleje ze wzrostem liczby atomowej do około 0,39 dla
i nieznacznie maleje ze wzrostem liczby atomowej do około 0,39 dla 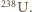 Wyjątek (patrz (a)) stanowi wodór, który niemal wyłącznie występuje jako izotop
Wyjątek (patrz (a)) stanowi wodór, który niemal wyłącznie występuje jako izotop 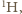 ale stanowi on niewielką część masy otaczających nas substancji (np. tylko 10% masy wody). Zatem dla otaczającej nas materii wynik jest taki sam, jak dla naszego ciała.
ale stanowi on niewielką część masy otaczających nas substancji (np. tylko 10% masy wody). Zatem dla otaczającej nas materii wynik jest taki sam, jak dla naszego ciała.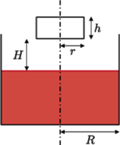
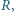 częściowo wypełnionego cieczą, wpada klocek w kształcie walca o promieniu
częściowo wypełnionego cieczą, wpada klocek w kształcie walca o promieniu  i wysokości
i wysokości 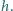 W chwili początkowej odległość dolnej powierzchni klocka od powierzchni cieczy wynosi
W chwili początkowej odległość dolnej powierzchni klocka od powierzchni cieczy wynosi 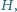 a jego prędkość jest równa zeru. Ile ciepła wydzieli się do chwili, gdy ustanie ruch klocka i cieczy? Gęstość klocka wynosi
a jego prędkość jest równa zeru. Ile ciepła wydzieli się do chwili, gdy ustanie ruch klocka i cieczy? Gęstość klocka wynosi 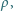 gęstość cieczy
gęstość cieczy 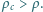
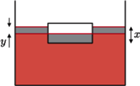
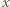 głębokość zanurzenia klocka po ustaleniu się równowagi, a przez
głębokość zanurzenia klocka po ustaleniu się równowagi, a przez 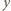 wzrost poziomu cieczy w naczyniu. Zgodnie z prawem Archimedesa
wzrost poziomu cieczy w naczyniu. Zgodnie z prawem Archimedesa 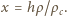 Z rysunku widać, że zachodzi związek
Z rysunku widać, że zachodzi związek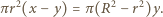
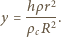
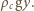 Zatem zachodzi związek
Zatem zachodzi związek 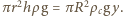 Po ustaleniu się równowagi energia potencjalna klocka zmalała o wielkość
Po ustaleniu się równowagi energia potencjalna klocka zmalała o wielkość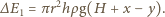
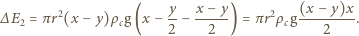
![1 hρ r2 Q = ∆E1 −∆ E2 =-πr2ρgh [H+ ---(1 − -2)] . 2 2ρc R](/math/temat/fizyka/plyny/zadania/2015/12/30/zf-k44-611/10x-347e3330a084016bdaec8cb9d22de6f1b7c693d4-dm-66,57,43-FF,FF,FF.gif)
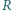 obraca się ruchem jednostajnym w płaszczyźnie pionowej wokół nieruchomej osi. Prędkość punktów na obwodzie koła wynosi
obraca się ruchem jednostajnym w płaszczyźnie pionowej wokół nieruchomej osi. Prędkość punktów na obwodzie koła wynosi 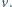 Znaleźć granicę obszaru suchego.
Znaleźć granicę obszaru suchego.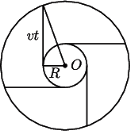


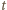 znajdowały się na okręgu o środku w punkcie
znajdowały się na okręgu o środku w punkcie 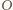 (
(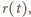 przy czym
przy czym 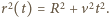 W polu ciężkości środek okręgu obniża się i w czasie
W polu ciężkości środek okręgu obniża się i w czasie 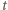 przebywa drogę
przebywa drogę 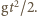 Granica obszaru suchego jest obwiednią okręgów, na których znajdują się w kolejnych momentach krople, które oderwały się jednocześnie od obręczy. Przyjmijmy, że początek układu współrzędnych znajduje się w środku obracającego się koła. Równanie "spadającego" okręgu ma w chwili
Granica obszaru suchego jest obwiednią okręgów, na których znajdują się w kolejnych momentach krople, które oderwały się jednocześnie od obręczy. Przyjmijmy, że początek układu współrzędnych znajduje się w środku obracającego się koła. Równanie "spadającego" okręgu ma w chwili 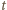 postać:
postać: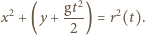
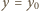 (
(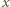 odpowiadającej jednemu z okręgów przecinających tę prostą:
odpowiadającej jednemu z okręgów przecinających tę prostą: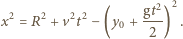
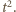 Jego wartość maksymalna
Jego wartość maksymalna 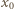 spełnia równanie:
spełnia równanie: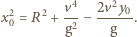
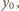 otrzymujemy równanie krzywej opisującej granicę "suchego" obszaru:
otrzymujemy równanie krzywej opisującej granicę "suchego" obszaru: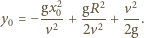
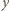 na wysokości
na wysokości 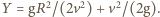 Gdy
Gdy 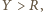 czyli spełniony jest warunek
czyli spełniony jest warunek 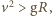 poszukiwana krzywa leży na zewnątrz obręczy. W przeciwnym przypadku granica "mokrego" obszaru przebiega w górnej części po obręczy (
poszukiwana krzywa leży na zewnątrz obręczy. W przeciwnym przypadku granica "mokrego" obszaru przebiega w górnej części po obręczy (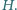 Pchnięcie naczynia w kierunku równoległym do jego ściany bocznej o długości
Pchnięcie naczynia w kierunku równoległym do jego ściany bocznej o długości 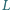 wywołuje kołysanie wody, której powierzchnia pozostaje niemal doskonale płaska. Ile, w przybliżeniu, wynosi okres takich drgań? Zakładamy, że podczas drgań zmiany położenia powierzchni wody są małe w porównaniu z
wywołuje kołysanie wody, której powierzchnia pozostaje niemal doskonale płaska. Ile, w przybliżeniu, wynosi okres takich drgań? Zakładamy, że podczas drgań zmiany położenia powierzchni wody są małe w porównaniu z 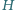 i
i 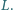 Przyspieszenie ziemskie wynosi
Przyspieszenie ziemskie wynosi 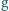 .
.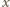 równoległej do
równoległej do 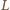 oraz osi
oraz osi 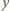 skierowanej pionowo w górę. Środek ciężkości wody przez cały czas ruchu pozostaje w jednakowej odległości od pionowych ścian akwarium równoległych do płaszczyzny
skierowanej pionowo w górę. Środek ciężkości wody przez cały czas ruchu pozostaje w jednakowej odległości od pionowych ścian akwarium równoległych do płaszczyzny 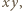 a okres badanych drgań nie zależy od szerokości naczynia. Podczas drgań, gdy na bocznej ściance o współrzędnej
a okres badanych drgań nie zależy od szerokości naczynia. Podczas drgań, gdy na bocznej ściance o współrzędnej 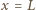 woda podnosi się na wysokość
woda podnosi się na wysokość 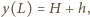 to na ściance
to na ściance 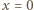 opada do
opada do 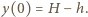 Środek ciężkości wody przesuwa się wówczas z położenia równowagi
Środek ciężkości wody przesuwa się wówczas z położenia równowagi 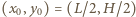 w położenie:
w położenie: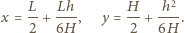
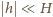 oraz
oraz 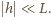 Wyprowadzając powyższe wyrażenia, skorzystaliśmy z faktu, że dla każdego
Wyprowadzając powyższe wyrażenia, skorzystaliśmy z faktu, że dla każdego 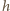 rozkład wody w naczyniu możemy otrzymać, dodając do rozkładu równowagowego wodę wypełniającą prostopadłościan o podstawie trójkąta prostokątnego z poziomą przyprostokątną
rozkład wody w naczyniu możemy otrzymać, dodając do rozkładu równowagowego wodę wypełniającą prostopadłościan o podstawie trójkąta prostokątnego z poziomą przyprostokątną 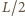 i pionową
i pionową 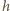 - po stronie
- po stronie 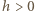 i odejmując taki sam prostopadłościan po stronie
i odejmując taki sam prostopadłościan po stronie 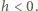 Pamiętamy też, że środek ciężkości jednorodnego trójkąta leży na przecięciu środkowych jego boków - dla trójkąta prostokątnego rzuty prostokątne środka ciężkości wypadają w 1/3 odpowiednich przyprostokątnych, licząc od wierzchołka kąta prostego. Kwadrat prędkości ruchu środka masy wynosi więc:
Pamiętamy też, że środek ciężkości jednorodnego trójkąta leży na przecięciu środkowych jego boków - dla trójkąta prostokątnego rzuty prostokątne środka ciężkości wypadają w 1/3 odpowiednich przyprostokątnych, licząc od wierzchołka kąta prostego. Kwadrat prędkości ruchu środka masy wynosi więc: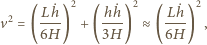
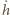 oznacza pochodną
oznacza pochodną 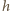 względem czasu. Jako kolejne przybliżenie przyjmijmy, że cała masa
względem czasu. Jako kolejne przybliżenie przyjmijmy, że cała masa 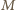 wody porusza się z tą sama prędkością
wody porusza się z tą sama prędkością 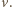 Wówczas zmiany całkowitej energii mechanicznej
Wówczas zmiany całkowitej energii mechanicznej 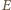 podczas ruchu możemy zapisać jako:
podczas ruchu możemy zapisać jako: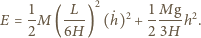
 zawieszonej na sprężynie o stałej sprężystości
zawieszonej na sprężynie o stałej sprężystości 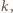 jeśli przyjmiemy:
jeśli przyjmiemy: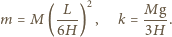
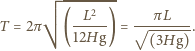
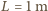 i
i 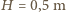
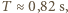 natomiast, na przykład, dla Jeziora Genewskiego, dla którego można przyjąć
natomiast, na przykład, dla Jeziora Genewskiego, dla którego można przyjąć 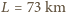 i średnią głębokość
i średnią głębokość 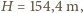 obliczone
obliczone 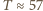 minut (obserwowano fale o
minut (obserwowano fale o 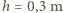 i
i 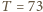 minuty).
minuty).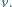 Przy jakiej prędkości
Przy jakiej prędkości  ruchu łopatek koła elektrownia osiąga maksymalną moc? Dla uproszczenia pomińmy efekty związane z zanurzaniem i wynurzaniem łopatek i zmiany ich ustawienia względem prędkości rzeki.
ruchu łopatek koła elektrownia osiąga maksymalną moc? Dla uproszczenia pomińmy efekty związane z zanurzaniem i wynurzaniem łopatek i zmiany ich ustawienia względem prędkości rzeki.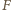 działająca na łopatkę będzie miała postać:
działająca na łopatkę będzie miała postać: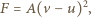
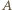 zależy od kształtu opływanego ciała, jego rozmiarów i od gęstości cieczy. "Pobierana" przez koło moc
zależy od kształtu opływanego ciała, jego rozmiarów i od gęstości cieczy. "Pobierana" przez koło moc 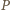 będzie więc równa:
będzie więc równa: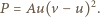
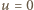 lub
lub  Pochodna
Pochodna 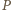 względem
względem  :
: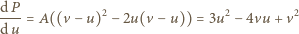
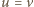 oraz dla
oraz dla 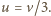 Jak łatwo sprawdzić, maksymalna moc osiągana jest dla
Jak łatwo sprawdzić, maksymalna moc osiągana jest dla 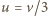 i wynosi:
i wynosi: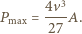
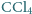 i woda. Pod ciśnieniem normalnym
i woda. Pod ciśnieniem normalnym 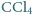 wrze w temperaturze
wrze w temperaturze 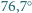 C. W wyniku równomiernego ogrzewania szklanki w kąpieli wodnej, w temperaturze
C. W wyniku równomiernego ogrzewania szklanki w kąpieli wodnej, w temperaturze 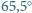 rozpoczyna się wrzenie na granicy rozdziału cieczy. Jaki jest stosunek mas czterochlorku węgla i wody, które wykipią w określonym czasie przy takim "granicznym" wrzeniu? Ciśnienie pary nasyconej wody w temperaturze
rozpoczyna się wrzenie na granicy rozdziału cieczy. Jaki jest stosunek mas czterochlorku węgla i wody, które wykipią w określonym czasie przy takim "granicznym" wrzeniu? Ciśnienie pary nasyconej wody w temperaturze 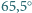 wynosi
wynosi 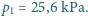
 znajduje się nasycona para wodna oraz nasycona para czterochlorku węgla, przy czym suma ich ciśnień cząstkowych równa jest ciśnieniu atmosferycznemu
znajduje się nasycona para wodna oraz nasycona para czterochlorku węgla, przy czym suma ich ciśnień cząstkowych równa jest ciśnieniu atmosferycznemu 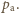 Stąd ciśnienie pary nasyconej CCl
Stąd ciśnienie pary nasyconej CCl  wynosi
wynosi 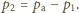 W czasie wrzenia pęcherzyki unoszą się w górę, dochodzą do powierzchni cieczy i pękają. Zatem stosunek mas czterochlorku węgla i wody, które wyparują w określonym czasie, równy jest stosunkowi gęstości par tych substancji
W czasie wrzenia pęcherzyki unoszą się w górę, dochodzą do powierzchni cieczy i pękają. Zatem stosunek mas czterochlorku węgla i wody, które wyparują w określonym czasie, równy jest stosunkowi gęstości par tych substancji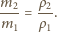
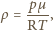
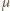 jest masą molową substancji, otrzymujemy:
jest masą molową substancji, otrzymujemy: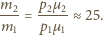

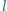 porusza się z prędkością
porusza się z prędkością 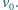 Z jaką prędkością
Z jaką prędkością  względem Ziemi należy popchnąć mały klocek z końca transportera przeciwnie do ruchu taśmy, aby ilość ciepła wydzielona w wyniku tarcia klocka o taśmę była największa? Jaka jest wartość tego ciepła, jeżeli współczynnik tarcia wynosi
względem Ziemi należy popchnąć mały klocek z końca transportera przeciwnie do ruchu taśmy, aby ilość ciepła wydzielona w wyniku tarcia klocka o taśmę była największa? Jaka jest wartość tego ciepła, jeżeli współczynnik tarcia wynosi 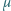 i spełniony jest warunek
i spełniony jest warunek 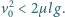
 otrzymujemy z zależności
otrzymujemy z zależności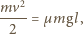
 jest masą klocka. Stąd
jest masą klocka. Stąd 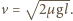 Po zatrzymaniu klocek zaczyna poruszać się z przyspieszeniem
Po zatrzymaniu klocek zaczyna poruszać się z przyspieszeniem 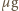 w kierunku ruchu taśmy. Prędkość taśmy osiągnie po czasie
w kierunku ruchu taśmy. Prędkość taśmy osiągnie po czasie 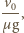 gdy przebędzie względem Ziemi drogę
gdy przebędzie względem Ziemi drogę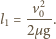
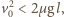 klocek osiągnie prędkość
klocek osiągnie prędkość 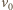 względem Ziemi, czyli zatrzyma się względem taśmy, zanim spadnie z transportera. Energia kinetyczna klocka w układzie związanym z taśmą transportera od chwili startu do chwili zatrzymania maleje o wielkość
względem Ziemi, czyli zatrzyma się względem taśmy, zanim spadnie z transportera. Energia kinetyczna klocka w układzie związanym z taśmą transportera od chwili startu do chwili zatrzymania maleje o wielkość 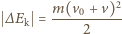 i tyle wynosi maksymalne ciepło wydzielone w układzie:
i tyle wynosi maksymalne ciepło wydzielone w układzie: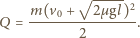
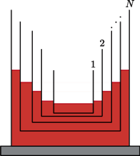
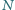 cylindrycznych naczyń o masach
cylindrycznych naczyń o masach 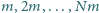 i przekrojach poprzecznych
i przekrojach poprzecznych 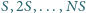 umieszczono jedno w drugim jak na rysunku. Do naczyń nalano tyle wody, że każde z nich pływa w większym naczyniu nie dotykając jego dna i ścianek. Największe naczynie stoi na stole. Do jakiej wysokości, w stosunku do powierzchni stołu, jest napełnione największe naczynie? Całkowita masa wody wynosi
umieszczono jedno w drugim jak na rysunku. Do naczyń nalano tyle wody, że każde z nich pływa w większym naczyniu nie dotykając jego dna i ścianek. Największe naczynie stoi na stole. Do jakiej wysokości, w stosunku do powierzchni stołu, jest napełnione największe naczynie? Całkowita masa wody wynosi 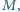 a jej gęstość wynosi
a jej gęstość wynosi 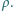 Ścianki naczyń uznać za zaniedbywalnie cienkie.
Ścianki naczyń uznać za zaniedbywalnie cienkie.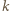 -tego naczynia. Z prawa Archimedesa wynika, że jeżeli wyjmiemy (w myśli) wszystkie naczynia pływające w
-tego naczynia. Z prawa Archimedesa wynika, że jeżeli wyjmiemy (w myśli) wszystkie naczynia pływające w 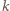 -tym naczyniu i dolejemy do niego tyle cieczy, aby zachować jej poziom wyjściowy, to siły działające na dno i ścianki naczynia ze strony cieczy w której ono pływa nie ulegną zmianie. Na
-tym naczyniu i dolejemy do niego tyle cieczy, aby zachować jej poziom wyjściowy, to siły działające na dno i ścianki naczynia ze strony cieczy w której ono pływa nie ulegną zmianie. Na 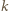 -te naczynie działa siła ciężkości
-te naczynie działa siła ciężkości 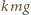 (
( 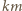 - masa tego naczynia), ciężar nalanej do niego wody
- masa tego naczynia), ciężar nalanej do niego wody 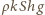 (
( 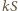 - pole powierzchni dna,
- pole powierzchni dna, 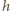 - wysokość poziomu wody w tym naczyniu) i siła wyporu
- wysokość poziomu wody w tym naczyniu) i siła wyporu 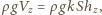 gdzie
gdzie 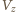 - objętość zanurzonej części naczynia,
- objętość zanurzonej części naczynia, 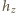 - głębokość zanurzenia.
- głębokość zanurzenia.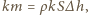 gdzie
gdzie 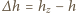 - różnica poziomów wody w rozpatrywanym naczyniu i w naczyniu w którym rozpatrywane naczynie pływa. Stąd
- różnica poziomów wody w rozpatrywanym naczyniu i w naczyniu w którym rozpatrywane naczynie pływa. Stąd 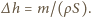 Wynika z tego, że różnica poziomów wody w dwóch dowolnych, sąsiednich naczyniach jest dla wszystkich naczyń taka sama. Przyjmijmy, że poziom wody w naczyniu stojącym na stole wynosi
Wynika z tego, że różnica poziomów wody w dwóch dowolnych, sąsiednich naczyniach jest dla wszystkich naczyń taka sama. Przyjmijmy, że poziom wody w naczyniu stojącym na stole wynosi 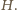 W następnym naczyniu wynosi on
W następnym naczyniu wynosi on 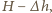 w kolejnym
w kolejnym 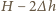 itd. Całkowita objętość wody w naczyniach wynosi
itd. Całkowita objętość wody w naczyniach wynosi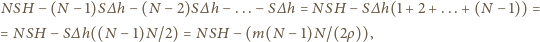
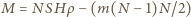
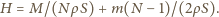
 poruszającego się z prędkością
poruszającego się z prędkością  po orbicie kołowej w pobliżu powierzchni Ziemi działa stała siła hamująca
po orbicie kołowej w pobliżu powierzchni Ziemi działa stała siła hamująca 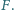 Znając przyspieszenie ziemskie
Znając przyspieszenie ziemskie 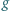 znaleźć prędkość
znaleźć prędkość 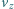 zniżania się satelity, przyjmując, że zmiana jego orbity zachodzi dostatecznie wolno.
zniżania się satelity, przyjmując, że zmiana jego orbity zachodzi dostatecznie wolno.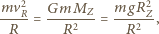
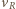 - prędkość satelity na orbicie kołowej o promieniu
- prędkość satelity na orbicie kołowej o promieniu 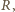
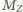 - masa Ziemi,
- masa Ziemi, 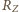 - jej promień. Załóżmy, że w ciągu krótkiego czasu
- jej promień. Załóżmy, że w ciągu krótkiego czasu 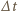 promień orbity zmniejszył się o
promień orbity zmniejszył się o 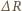 pod wpływem siły
pod wpływem siły 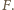 Z zasady zachowania energii mamy związek
Z zasady zachowania energii mamy związek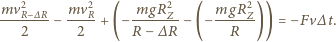
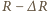 z prędkością
z prędkością 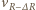 ma postać
ma postać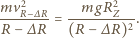
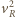 i
i 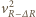 z zależności (1) i (3) i podstawiając je do zależności (2) otrzymujemy
z zależności (1) i (3) i podstawiając je do zależności (2) otrzymujemy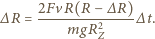
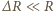 oraz
oraz 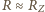 znajdujemy prędkość zniżania się satelity
znajdujemy prędkość zniżania się satelity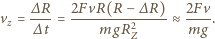
 może obracać się wokół pionowej osi, pokrywającej się z jego średnicą. W środku pierścienia umieszczono małą igiełkę magnetyczną, która może swobodnie obracać się wokół tej samej osi. Gdy pierścień jest nieruchomy, igiełka ustawia się wzdłuż składowej poziomej pola magnetycznego Ziemi
może obracać się wokół pionowej osi, pokrywającej się z jego średnicą. W środku pierścienia umieszczono małą igiełkę magnetyczną, która może swobodnie obracać się wokół tej samej osi. Gdy pierścień jest nieruchomy, igiełka ustawia się wzdłuż składowej poziomej pola magnetycznego Ziemi 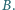 Pierścień wprowadzono w bardzo szybki ruch obrotowy ze stałą prędkością kątową
Pierścień wprowadzono w bardzo szybki ruch obrotowy ze stałą prędkością kątową 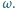 O jaki kąt odchyliła się igiełka od swego początkowego ustawienia? Opór pierścienia wynosi
O jaki kąt odchyliła się igiełka od swego początkowego ustawienia? Opór pierścienia wynosi 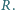
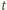 wynosi
wynosi 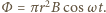 W pierścieniu powstaje prąd indukcyjny o natężeniu
W pierścieniu powstaje prąd indukcyjny o natężeniu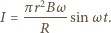
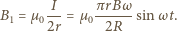
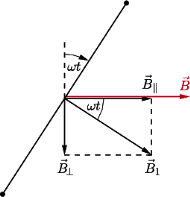
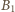 na składowe - równoległą i prostopadłą do wektora
na składowe - równoległą i prostopadłą do wektora 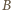 (
(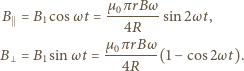
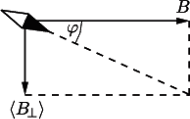
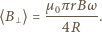
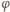 (
(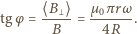

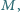 do którego przymocowany jest nieważki, nieruchomy bloczek, może ślizgać się po poziomej powierzchni. Przez bloczek przerzucona jest nić, której jeden koniec jest poziomy i przymocowany do ściany, a na drugim końcu zawieszony jest ciężarek. W chwili początkowej ciężarek odchylono od pionu o kąt
do którego przymocowany jest nieważki, nieruchomy bloczek, może ślizgać się po poziomej powierzchni. Przez bloczek przerzucona jest nić, której jeden koniec jest poziomy i przymocowany do ściany, a na drugim końcu zawieszony jest ciężarek. W chwili początkowej ciężarek odchylono od pionu o kąt 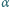 i puszczono. Znaleźć masę ciężarka, jeśli kąt odchylenia nici od pionu nie zmienia się podczas ruchu klocka. Tarcie zaniedbujemy.
i puszczono. Znaleźć masę ciężarka, jeśli kąt odchylenia nici od pionu nie zmienia się podczas ruchu klocka. Tarcie zaniedbujemy.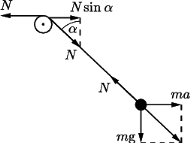
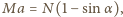 gdzie
gdzie 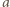 jest przyspieszeniem klocka, a
jest przyspieszeniem klocka, a 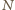 siłą naprężenia nici. W układzie związanym z klockiem ciężarek porusza się z przyspieszeniem
siłą naprężenia nici. W układzie związanym z klockiem ciężarek porusza się z przyspieszeniem 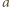 wzdłuż prostej, która tworzy z pionem kąt
wzdłuż prostej, która tworzy z pionem kąt 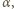 pod działaniem sił przedstawionych na rysunku obok. Jego równanie ruchu ma postać:
pod działaniem sił przedstawionych na rysunku obok. Jego równanie ruchu ma postać: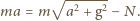
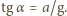 Rozwiązując przedstawione równania, otrzymujmy masę ciężarka:
Rozwiązując przedstawione równania, otrzymujmy masę ciężarka: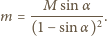

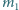 i
i 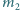 związane są nicią o długości
związane są nicią o długości 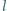 i poruszają się bez tarcia po powierzchni poziomej. W pewnej chwili okazało się, że ciało o masie
i poruszają się bez tarcia po powierzchni poziomej. W pewnej chwili okazało się, że ciało o masie 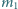 jest nieruchome, a prędkość ciała o masie
jest nieruchome, a prędkość ciała o masie 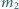 ma wartość
ma wartość  i jest prostopadła do nici. Jakie jest w tym momencie naprężenie nici?
i jest prostopadła do nici. Jakie jest w tym momencie naprężenie nici?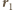 i
i 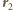 spełniają związki:
spełniają związki: 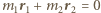 oraz
oraz 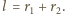 Stąd
Stąd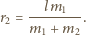
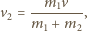
 jest prędkością względną ciał. Szukane naprężenie nici dane jest wzorem:
jest prędkością względną ciał. Szukane naprężenie nici dane jest wzorem: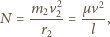
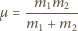

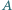 i
i 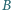 w obwodzie przedstawionym na rysunku. Opór każdej krawędzi między węzłami wynosi
w obwodzie przedstawionym na rysunku. Opór każdej krawędzi między węzłami wynosi 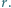 Sieć jest nieskończona w obie strony.
Sieć jest nieskończona w obie strony.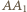 i
i 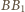 :
:
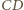 i
i 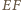 są jednakowe i równe
są jednakowe i równe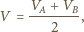
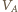 i
i 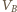 są potencjałami punktów
są potencjałami punktów 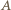 i
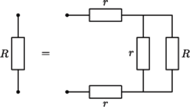
i 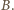 Zatem krawędzie między tymi węzłami można usunąć. Równoważny obwód składa się z dwóch nieskończonych obwodów połączonych równolegle i równoległego do nich opornika
Zatem krawędzie między tymi węzłami można usunąć. Równoważny obwód składa się z dwóch nieskończonych obwodów połączonych równolegle i równoległego do nich opornika  Opór
Opór 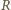 każdego z nieskończonych obwodów nie zmieni się, gdy dodamy do niego jeden z powtarzających się elementów. Wynika stąd równanie:
każdego z nieskończonych obwodów nie zmieni się, gdy dodamy do niego jeden z powtarzających się elementów. Wynika stąd równanie: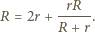
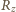 całego obwodu otrzymujemy z równania:
całego obwodu otrzymujemy z równania: