Zadanie ZF-790
o zadaniu...
- Publikacja w Delcie: czerwiec 2011
- Publikacja elektroniczna: 31 maja 2011
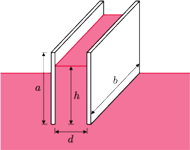
Do dużego naczynia nalana jest ciecz o gęstości
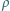 i przenikalności
elektrycznej
i przenikalności
elektrycznej
 . Dwie pionowe równoległe płyty stykają się krawędziami
z powierzchnią cieczy. Płyty mają wymiary
. Dwie pionowe równoległe płyty stykają się krawędziami
z powierzchnią cieczy. Płyty mają wymiary
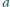 i
i
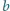 , odległość między
nimi wynosi
, odległość między
nimi wynosi
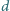 . Płyty naładowano do różnicy potencjałów
. Płyty naładowano do różnicy potencjałów
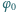 i odłączono od źródła. Na jaką wysokość
i odłączono od źródła. Na jaką wysokość
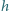 wzniesie się
ciecz?
wzniesie się
ciecz?
Na lince zawieszono ciężar o masie
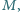 a linkę przełożono
przez nieruchomy walec o promieniu
a linkę przełożono
przez nieruchomy walec o promieniu
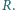 Na drugim końcu linki
zawieszono najmniejszy ciężar
Na drugim końcu linki
zawieszono najmniejszy ciężar
 wystarczający do tego, aby
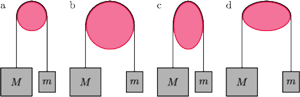
większy ciężar nie ześlizgnął się w dół (Rys. a). Jeśli ten sam ciężar
wystarczający do tego, aby
większy ciężar nie ześlizgnął się w dół (Rys. a). Jeśli ten sam ciężar
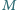 zawiesić na:
zawiesić na:
to czy niezbędny ciężar
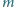 będzie mniejszy niż na rysunku a, większy, czy
taki sam? Współczynnik tarcia linki o podporę jest w każdym przypadku
jednakowy.
będzie mniejszy niż na rysunku a, większy, czy
taki sam? Współczynnik tarcia linki o podporę jest w każdym przypadku
jednakowy.
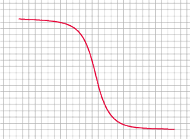
Źródło dźwięku o stałej częstotliwości poruszało się ruchem jednostajnym
po linii prostej przebiegającej w pewnej odległości od nieruchomego
mikrofonu. Wykonano staranny pomiar zależności częstotliwości
rejestrowanej przez mikrofon od czasu odebrania sygnału i zapisano wykres
 na papierze milimetrowym. Niestety, zapomniano oznaczyć osie,
wskutek czego arkusz papieru mógł zostać obrócony. Czy wykres jest
symetryczny względem obrotu o
na papierze milimetrowym. Niestety, zapomniano oznaczyć osie,
wskutek czego arkusz papieru mógł zostać obrócony. Czy wykres jest
symetryczny względem obrotu o
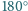 ? Jeśli nie, to czy można
rozstrzygnąć, czy jest on prawidłowy w danej postaci, czy też należy go
obrócić? Załączony rysunek jest tylko ilustracją problemu, a nie informacją
o dokładnym przebiegu wykresu.
? Jeśli nie, to czy można
rozstrzygnąć, czy jest on prawidłowy w danej postaci, czy też należy go
obrócić? Załączony rysunek jest tylko ilustracją problemu, a nie informacją
o dokładnym przebiegu wykresu.
Ile wody należy wlać do naczynia, by środek ciężkości naczynia z wodą leżał możliwie najniżej?
W naczyniu z wodą zanurzamy pionowo drewniany klocek o przekroju
kwadratowym
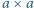
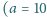 cm) i długości
cm) i długości
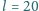 cm. Jaka
ilość ciepła wydzieli się w wyniku przewrócenia się tego klocka?
Przyjmujemy, że gęstość drewna jest równa połowie gęstości wody.
cm. Jaka
ilość ciepła wydzieli się w wyniku przewrócenia się tego klocka?
Przyjmujemy, że gęstość drewna jest równa połowie gęstości wody.
W zjawisku Comptona obserwuje się promieniowanie rentgenowskie
rozproszone na swobodnych elektronach, przy czym zwykle zakłada się, że
początkowo elektrony były nieruchome. Przyjmijmy, że rozproszenie
następuje na elektronach w atomach wodoru, będących początkowo w stanie
podstawowym. Ile wynosi poszerzenie zakresu długości fali promieniowania
rozproszonego wstecz (
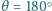 ), wynikające z ruchu elektronów?
Wystarczy wynik przybliżony oparty na modelu Bohra, dla długości fali
promieniowania padającego równej
), wynikające z ruchu elektronów?
Wystarczy wynik przybliżony oparty na modelu Bohra, dla długości fali
promieniowania padającego równej
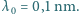
Rurka składa się z pięciu pionowych segmentów wysokości
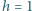 m
i jednego segmentu dłuższego. Jeśli początkowo rurka nie zawierała wody, to
do jakiej wysokości należy jej nalać do dłuższego segmentu, żeby zaczęła
wyciekać drugim końcem? Średnica rurki jest znacznie mniejsza od
m
i jednego segmentu dłuższego. Jeśli początkowo rurka nie zawierała wody, to
do jakiej wysokości należy jej nalać do dłuższego segmentu, żeby zaczęła
wyciekać drugim końcem? Średnica rurki jest znacznie mniejsza od
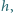 ale na tyle duża, że przepływ wody i przepływ powietrza mogą w niej
zachodzić niezależnie. Temperatura powietrza w rurce się nie zmienia,
a ciśnienie atmosferyczne wynosi
ale na tyle duża, że przepływ wody i przepływ powietrza mogą w niej
zachodzić niezależnie. Temperatura powietrza w rurce się nie zmienia,
a ciśnienie atmosferyczne wynosi
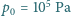 .
.
Równoległa wiązka światła o natężeniu (tzn. mocy na jednostkę powierzchni
prostopadłej)
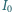 pada na kulkę o promieniu
pada na kulkę o promieniu
 ze szkła
o współczynniku załamania
ze szkła
o współczynniku załamania
 W odległości
W odległości
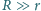 od kulki
znajduje się ekran prostopadły do wiązki padającej, ale oświetlony tylko przez
światło przechodzące przez kulkę. Jeśli można pominąć efekty dyfrakcyjne i
odbicie światła od szkła, to jakie jest natężenie światła padającego na środek
ekranu?
od kulki
znajduje się ekran prostopadły do wiązki padającej, ale oświetlony tylko przez
światło przechodzące przez kulkę. Jeśli można pominąć efekty dyfrakcyjne i
odbicie światła od szkła, to jakie jest natężenie światła padającego na środek
ekranu?

Sprężyście zginający się jednorodny pręt o długości
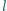 i masie
i masie
 zamocowano jednym końcem poziomo, a drugi zwisa pod wpływem siły
ciężkości. Miarą sztywności pręta jest dany parametr
zamocowano jednym końcem poziomo, a drugi zwisa pod wpływem siły
ciężkości. Miarą sztywności pręta jest dany parametr
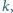 będący
stosunkiem momentu siły zginającej
będący
stosunkiem momentu siły zginającej
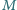 do kąta
do kąta
 między stycznymi
do końców pręta, gdy
między stycznymi
do końców pręta, gdy
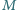 ma wzdłuż niego stałą wartość. Obliczyć
numerycznie zwis pręta
ma wzdłuż niego stałą wartość. Obliczyć
numerycznie zwis pręta
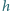 oraz kąt opadania jego końca
oraz kąt opadania jego końca
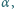 przy
następujących danych:
przy
następujących danych:
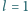 m,
m,
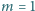 kg,
kg,
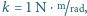 przyspieszenie ziemskie
przyspieszenie ziemskie
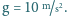
Mała kulka o masie
 i ładunku elektrycznym
i ładunku elektrycznym
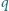 wisi na
sprężynie o stałej sprężystości
wisi na
sprężynie o stałej sprężystości
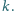 Kulka jest utrzymywana na
wysokości
Kulka jest utrzymywana na
wysokości
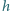 nad ziemią, tak że sprężyna nie jest naciągnięta.
Na podłodze, dokładnie pod kulką, znajduje się druga kulka, o takiej samej
masie
nad ziemią, tak że sprężyna nie jest naciągnięta.
Na podłodze, dokładnie pod kulką, znajduje się druga kulka, o takiej samej
masie
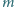 i przeciwnym ładunku
i przeciwnym ładunku
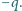 W pewnej chwili puszczamy
górną kulkę. Dla jakiego minimalnego ładunku
W pewnej chwili puszczamy
górną kulkę. Dla jakiego minimalnego ładunku
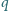 dolna kulka zostanie
poderwana do góry? Stała sprężystości sprężyny i masa kulki spełniają
warunek
dolna kulka zostanie
poderwana do góry? Stała sprężystości sprężyny i masa kulki spełniają
warunek
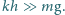
Kulka o masie
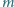 i ładunku elektrycznym
i ładunku elektrycznym
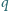 znajduje się pod
unieruchomionym ciałem o ładunku
znajduje się pod
unieruchomionym ciałem o ładunku
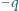 w odległości
w odległości
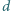 od niego
i na wysokości
od niego
i na wysokości
 nad ziemią. Jaką minimalną prędkość skierowaną
pionowo w dół należy nadać kulce, aby upadła na ziemię? Początkowa
wysokość
nad ziemią. Jaką minimalną prędkość skierowaną
pionowo w dół należy nadać kulce, aby upadła na ziemię? Początkowa
wysokość
 jest duża w porównaniu z
jest duża w porównaniu z
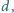 ruch odbywa się
w jednorodnym polu ciążenia Ziemi.
ruch odbywa się
w jednorodnym polu ciążenia Ziemi.
Zbiornik zawierający
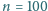 moli gazu doskonałego o temperaturze
moli gazu doskonałego o temperaturze
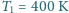 i pod ciśnieniem
i pod ciśnieniem
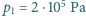 znajduje się
w otoczeniu powietrza atmosferycznego o temperaturze
znajduje się
w otoczeniu powietrza atmosferycznego o temperaturze
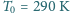 i pod
ciśnieniem
i pod
ciśnieniem
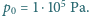 Obliczyć maksymalną pracę, którą może
wykonać zespół gaz + otoczenie (zarówno bezpośrednio, jak za
pośrednictwem maszyn cieplnych). Ciepło molowe gazu przy stałej objętości
jest równe
Obliczyć maksymalną pracę, którą może
wykonać zespół gaz + otoczenie (zarówno bezpośrednio, jak za
pośrednictwem maszyn cieplnych). Ciepło molowe gazu przy stałej objętości
jest równe
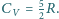
Pan Nowak wybiera się samochodem na urlop na południe i namawia do tego samego znajomych. Ma w tym pewien interes – oczekuje pewnego wydłużenia doby, a więc wydłużenia wakacji (przy niezmienionej cenie noclegów!). Udało mu się zebrać grupę 20 rodzin, którym skutecznie przedstawił przewagę Grecji nad Norwegią jako miejsca letniego wypoczynku. O ile wydłuży się doba wskutek tej wyprawy?

W płaskim naczyniu położono walec i nalano cieczy z jednej jego strony do
wysokości równej średnicy walca, a innej cieczy nalano z drugiej strony do
wysokości równej promieniowi walca. Przepływ cieczy wokół podstaw walca
jest uniemożliwiony barierami, które nie przeszkadzają walcowi toczyć się
w lewo lub w prawo. Jeśli gęstość walca jest równa
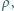 w opisanej
sytuacji pozostaje on w równowadze, a jego nacisk na dno naczynia jest równy
połowie jego ciężaru, to ile wynosi gęstość cieczy z lewej strony walca, a ile –
z prawej?
w opisanej
sytuacji pozostaje on w równowadze, a jego nacisk na dno naczynia jest równy
połowie jego ciężaru, to ile wynosi gęstość cieczy z lewej strony walca, a ile –
z prawej?
Obliczyć siłę rozciągającą kołową pętlę o promieniu 10 cm równomiernie
naładowaną ładunkiem
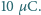 Pozostałe niezbędne dane ocenić
orientacyjnie. Pętla jest wykonana z drutu.
Pozostałe niezbędne dane ocenić
orientacyjnie. Pętla jest wykonana z drutu.
Lokomotywa jadąca po prostym torze ze stałą prędkością
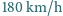 gwiżdże, wydając ton o częstotliwości 1000 Hz. W odległości 300 m od
toru stoi krowa. Ile wyniesie częstotliwość tonu słyszanego przez krowę
w momencie, gdy lokomotywa zbliży się do niej na odległość 500 m?
Prędkość dźwięku w powietrzu ma wartość
gwiżdże, wydając ton o częstotliwości 1000 Hz. W odległości 300 m od
toru stoi krowa. Ile wyniesie częstotliwość tonu słyszanego przez krowę
w momencie, gdy lokomotywa zbliży się do niej na odległość 500 m?
Prędkość dźwięku w powietrzu ma wartość
Dwóch studentów przechadzało się nad brzegiem stawu. W mętnej wodzie
podskakiwała szyjka butelki wrzuconej przez jakiegoś wandala.
– Założę się
o dychę, że potrafię obliczyć średnią głębokość zanurzenia tej butelki –
powiedział Fizyk.
– Ściemniasz, przecież nic nie widać w tej zupie!
– zaoponował Humanista. – Przyjmuję zakład!
Fizyk ustawił funkcję
stopera na swoim zegarku i zmierzył czas 10 okresów drgań butelki
– wyszło mu 7,8 sekundy. Przestawił zegarek na kalkulator i po paru
obliczeniach zawołał:
– Piętnaście centymetrów, sprawdzamy i jesteś do tyłu
o dychę!
Który student wygrał zakład?
Masa wolframowego włókna żarówki wynosi
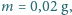 a ciepło
właściwe wolframu
a ciepło
właściwe wolframu
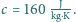 Gdy żarówka była zasilana
stałym napięciem 230 V, jej opór wynosił
Gdy żarówka była zasilana
stałym napięciem 230 V, jej opór wynosił
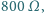 a temperatura
włókna była równa
a temperatura
włókna była równa
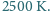 Podłączono tę żarówkę do napięcia
sinusoidalnie zmiennego o częstotliwości 50 Hz i wartości skutecznej 230 V.
Obliczyć przybliżoną głębokość modulacji promieniowania żarówki,
tzn. wielkość
Podłączono tę żarówkę do napięcia
sinusoidalnie zmiennego o częstotliwości 50 Hz i wartości skutecznej 230 V.
Obliczyć przybliżoną głębokość modulacji promieniowania żarówki,
tzn. wielkość
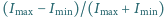 , gdzie
, gdzie
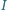 – moc
promieniowania. Założyć, że przepuszczalność szkła żarówki
nie zależy od długości fali.
– moc
promieniowania. Założyć, że przepuszczalność szkła żarówki
nie zależy od długości fali.
Można wykorzystać także następujące dane: gdy stałe napięcie zasilające
zmieniano w niewielkim zakresie i powoli, na każdy 1 wolt jego przyrostu
opór żarówki zwiększał się o
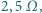 a temperatura włókna zwiększała
się o 0,7 K.
a temperatura włókna zwiększała
się o 0,7 K.
Pod wpływem różnicy ciśnień w rurce o stałym przekroju występuje stacjonarny (niezmienny w czasie) i laminarny (bezwirowy) przepływ cieczy. Jeśli dwukrotnie zwiększymy średnicę rurki, nie zmieniając jej długości, różnicy ciśnień i rodzaju cieczy, to ile razy wzrośnie ilość cieczy przepływającej w ciągu jednostki czasu? Uzasadnić odpowiedź.
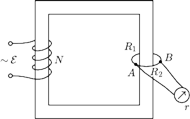
Jedno uzwojenie transformatora obniżającego napięcie ma
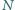 zwojów,
drugie jeden. Transformator ten podłączony jest do źródła napięcia zmiennego
o sile elektromotorycznej
zwojów,
drugie jeden. Transformator ten podłączony jest do źródła napięcia zmiennego
o sile elektromotorycznej
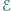 . Do pojedynczego uzwojenia podłączony jest
w punktach
. Do pojedynczego uzwojenia podłączony jest
w punktach
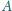 i
i
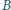 galwanometr o oporze wewnętrznym
galwanometr o oporze wewnętrznym
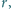 dzieląc zwój na części o oporze
dzieląc zwój na części o oporze
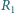 i
i
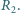 Jakie natężenie prądu
będzie pokazywał galwanometr?
Jakie natężenie prądu
będzie pokazywał galwanometr?

Pozioma płytka kołowa o promieniu
 i momencie bezwładności
i momencie bezwładności
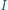 obraca się wokół swojej osi bez tarcia. Jej początkowa prędkość kątowa
to
obraca się wokół swojej osi bez tarcia. Jej początkowa prędkość kątowa
to
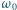 . W płytce jest rowek, a w rowku – kulka o masie
. W płytce jest rowek, a w rowku – kulka o masie
 , która
może się w nim toczyć bez tarcia. Kulka początkowo znajdowała się
w środku płytki, a pod wpływem bardzo słabego impulsu zaczęła się toczyć na
zewnątrz i spadła z płytki. Ile wynosiła końcowa prędkość kątowa
płytki
, która
może się w nim toczyć bez tarcia. Kulka początkowo znajdowała się
w środku płytki, a pod wpływem bardzo słabego impulsu zaczęła się toczyć na
zewnątrz i spadła z płytki. Ile wynosiła końcowa prędkość kątowa
płytki
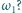 Rozważyć trzy przypadki – gdy rowek biegnie prosto
wzdłuż promienia (Rys. (a)) i gdy ma kształt półokręgu (Rys. (b) i (c)).
Rozważyć trzy przypadki – gdy rowek biegnie prosto
wzdłuż promienia (Rys. (a)) i gdy ma kształt półokręgu (Rys. (b) i (c)).