Klub 44F - zadania II 2012»Zadanie 533
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania II 2012
- Publikacja w Delcie: luty 2012
- Publikacja elektroniczna: 1 lutego 2012
- Artykuł źródłowy w wersji do druku [application/pdf]: (65 KB)
Wodór
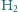 znajduje się w temperaturze 300 K pod ciśnieniem 100 Pa
w naczyniu o stałej objętości. Ile będzie wynosić ciśnienie w naczyniu,
jeśli ogrzać wodór do temperatury
znajduje się w temperaturze 300 K pod ciśnieniem 100 Pa
w naczyniu o stałej objętości. Ile będzie wynosić ciśnienie w naczyniu,
jeśli ogrzać wodór do temperatury
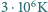 ?
?
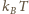 w temperaturze
w temperaturze
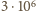 K
wynosi – w przeliczeniu na elektronowolty – około 300 eV, czyli znacznie więcej
zarówno od energii dysocjacji cząsteczek wodoru, jak i energii jonizacji
atomowego wodoru. Każda cząsteczka H
K
wynosi – w przeliczeniu na elektronowolty – około 300 eV, czyli znacznie więcej
zarówno od energii dysocjacji cząsteczek wodoru, jak i energii jonizacji
atomowego wodoru. Każda cząsteczka H
 rozpadnie się więc po
podgrzaniu na cztery cząstki – dwa jądra i dwa elektrony. Ciśnienie wzrośnie
rozpadnie się więc po
podgrzaniu na cztery cząstki – dwa jądra i dwa elektrony. Ciśnienie wzrośnie
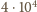 razy i wyniesie 4 MPa.
razy i wyniesie 4 MPa.
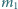 wisiał na sprężynce o stałej sprężystości
wisiał na sprężynce o stałej sprężystości
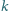 i drgał z amplitudą
i drgał z amplitudą
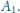 Z góry sypie się w tempie
Z góry sypie się w tempie
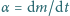 cienki strumień piasku, który spada ze stałą prędkością
cienki strumień piasku, który spada ze stałą prędkością
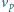 (stałą wskutek np. działania siły oporu powietrza). Piasek pada
na ciężarek i przykleja się, dalej drgając razem z nim. Po czasie długim
w porównaniu z okresem drgań masa ciężarka wraz z piaskiem wzrosła do
wartości
(stałą wskutek np. działania siły oporu powietrza). Piasek pada
na ciężarek i przykleja się, dalej drgając razem z nim. Po czasie długim
w porównaniu z okresem drgań masa ciężarka wraz z piaskiem wzrosła do
wartości
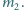 Znaleźć końcową amplitudę drgań. Założyć, że
prędkość ruchu ciężarka nie przekraczała prędkości spadku piasku.
Znaleźć końcową amplitudę drgań. Założyć, że
prędkość ruchu ciężarka nie przekraczała prędkości spadku piasku.
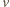 do góry, wtedy
jego prędkość względem piasku wynosi
do góry, wtedy
jego prędkość względem piasku wynosi
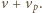 Ponieważ masa piasku
na jednostkę długości strumienia jest równa
Ponieważ masa piasku
na jednostkę długości strumienia jest równa
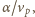 więc masa piasku
przyklejonego w ciągu czasu
więc masa piasku
przyklejonego w ciągu czasu
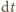 wynosi
wynosi
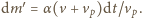 Energia
przekształcona w ciepło jest równa
Energia
przekształcona w ciepło jest równa
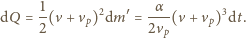
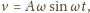 gdzie
gdzie
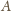 jest amplitudą,
jest amplitudą,
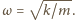 Gdy
podstawimy zależność
Gdy
podstawimy zależność
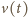 do
do
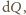 rozwiniemy sześcian
i scałkujemy względem okresu, niezerowy wkład do całki dadzą tylko parzyste
potęgi
rozwiniemy sześcian
i scałkujemy względem okresu, niezerowy wkład do całki dadzą tylko parzyste
potęgi
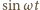 – zerowa i druga:
– zerowa i druga:
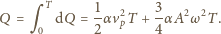
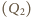 jest spadkiem
energii drgań w tym czasie. Przechodząc do dłuższej skali czasu, należy
wyrażenie
jest spadkiem
energii drgań w tym czasie. Przechodząc do dłuższej skali czasu, należy
wyrażenie
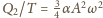 przyrównać do
przyrównać do
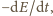 gdzie
gdzie
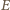 jest energią drgań ciężarka,
jest energią drgań ciężarka,
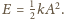 Stąd
Stąd
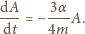
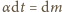 i scałkowanie prowadzi do wyniku
i scałkowanie prowadzi do wyniku
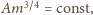 czyli
czyli
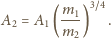
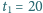 minut.
Po jakim dodatkowym czasie
minut.
Po jakim dodatkowym czasie
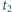 promień nawiniętej taśmy zmniejszy
się znowu dwukrotnie?
promień nawiniętej taśmy zmniejszy
się znowu dwukrotnie?
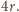 Zatem
po dwukrotnym zmniejszeniu się tego promienia powierzchnia nawiniętej
taśmy zmniejszy się o wielkość
Zatem
po dwukrotnym zmniejszeniu się tego promienia powierzchnia nawiniętej
taśmy zmniejszy się o wielkość
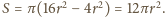 Przy
odsłuchiwaniu zapisu prędkość liniowa przesuwu taśmy
Przy
odsłuchiwaniu zapisu prędkość liniowa przesuwu taśmy
 jest stała,
zatem długość nawiniętej taśmy to
jest stała,
zatem długość nawiniętej taśmy to
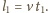 Z drugiej strony jest ona
równa
Z drugiej strony jest ona
równa
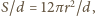 gdzie
gdzie
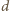 jest grubością taśmy.
Z porównania tych wzorów wynika, że
jest grubością taśmy.
Z porównania tych wzorów wynika, że
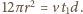
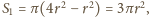 stąd
stąd
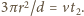 Ostatecznie:
Ostatecznie:
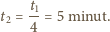
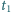 okazało się, że promień nawiniętej taśmy
okazało się, że promień nawiniętej taśmy
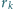 jest trzy razy większy od
początkowego promienia
jest trzy razy większy od
początkowego promienia
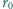 . W jakim czasie można nawinąć na
tę samą szpulę taśmę magnetyczną takiej samej długości, ale dwa razy
cieńszą?
. W jakim czasie można nawinąć na
tę samą szpulę taśmę magnetyczną takiej samej długości, ale dwa razy
cieńszą?
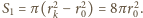 Zatem długość nawiniętej taśmy
będzie równa
Zatem długość nawiniętej taśmy
będzie równa
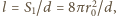 gdzie
gdzie
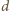 jest grubością taśmy.
jest grubością taśmy.
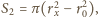 a jej długość wyniesie
a jej długość wyniesie
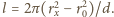 Ponieważ
długości taśm są jednakowe, to z porównania wzorów na nie wynika, że
Ponieważ
długości taśm są jednakowe, to z porównania wzorów na nie wynika, że
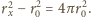 Stąd
Stąd
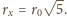
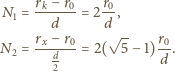
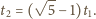
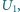 a obwód wtórny był otwarty, napięcie na uzwojeniu
wtórnym było równe
a obwód wtórny był otwarty, napięcie na uzwojeniu
wtórnym było równe
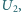 a natężenie prądu w uzwojeniu pierwotnym
a natężenie prądu w uzwojeniu pierwotnym
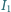 (wszystkie podane wielkości są wartościami skutecznymi).
Zamknięto obwód wtórny, dołączając do niego: a) opornik, b) zwojnicę
bezoporową, c) kondensator. Ile w każdym z tych przypadków wyniesie
natężenie prądu w uzwojeniu pierwotnym, jeśli we wtórnym popłynie prąd
o natężeniu
(wszystkie podane wielkości są wartościami skutecznymi).
Zamknięto obwód wtórny, dołączając do niego: a) opornik, b) zwojnicę
bezoporową, c) kondensator. Ile w każdym z tych przypadków wyniesie
natężenie prądu w uzwojeniu pierwotnym, jeśli we wtórnym popłynie prąd
o natężeniu
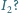 Oba napięcia
Oba napięcia
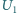 i
i
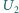 nie zmieniły
wartości, a straty energii w transformatorze (jego nagrzewanie się) można
pominąć.
nie zmieniły
wartości, a straty energii w transformatorze (jego nagrzewanie się) można
pominąć.
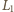 i
i
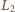 indukcyjności uzwojenia pierwotnego
i wtórnego, a przez
indukcyjności uzwojenia pierwotnego
i wtórnego, a przez
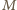 współczynnik indukcji wzajemnej. Równania
wyrażające II prawo Kirchhoffa dla obu obwodów przybierają postać
współczynnik indukcji wzajemnej. Równania
wyrażające II prawo Kirchhoffa dla obu obwodów przybierają postać
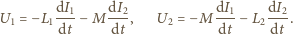
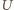 i
i
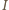 oznaczają –
niezbyt konsekwentnie – wartości chwilowe, w odróżnieniu od dalszych
przekształceń i treści zadania.
oznaczają –
niezbyt konsekwentnie – wartości chwilowe, w odróżnieniu od dalszych
przekształceń i treści zadania.
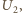 mimo zamknięcia obwodu wtórnego,
świadczy o tym, że sprzężenie indukcyjne obwodów jest maksymalne,
tzn.
mimo zamknięcia obwodu wtórnego,
świadczy o tym, że sprzężenie indukcyjne obwodów jest maksymalne,
tzn.
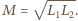 Wtedy stosunek
Wtedy stosunek
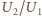 jest równy
jest równy
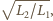 zatem stały. Przyjmując częstość
zatem stały. Przyjmując częstość
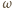 jako daną,
z danych wartości
jako daną,
z danych wartości
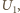
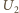 i
i
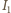 wyznaczamy (dla
wyznaczamy (dla
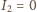 )
)
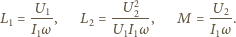
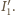 W przypadku a) należy
przyrównać
W przypadku a) należy
przyrównać
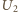 do
do
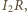 co po wyeliminowaniu przesunięcia
fazy między
co po wyeliminowaniu przesunięcia
fazy między
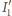 a
a
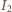 prowadzi do tożsamości
prowadzi do tożsamości
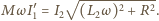
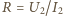 oraz
wyrażeń na
oraz
wyrażeń na
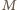 i
i
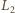 daje szukane natężenie prądu w uzwojeniu
pierwotnym
daje szukane natężenie prądu w uzwojeniu
pierwotnym
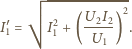
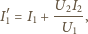
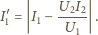
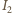 )
we wszystkich przypadkach przechodzimy do powszechnie znanego
związku
)
we wszystkich przypadkach przechodzimy do powszechnie znanego
związku
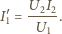
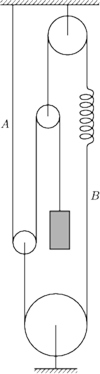
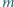 wisi na nici
wisi na nici
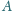 przełożonej przez 2 bloki
ruchome. Osie tych bloków są połączone nicią
przełożonej przez 2 bloki
ruchome. Osie tych bloków są połączone nicią
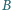 przełożoną przez
2 bloki nieruchome, a w tej nici zamontowana jest sprężynka o stałej
sprężystości
przełożoną przez
2 bloki nieruchome, a w tej nici zamontowana jest sprężynka o stałej
sprężystości
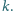 Obliczyć okres pionowych drgań ciężarka. Masy
bloków pominąć.
Obliczyć okres pionowych drgań ciężarka. Masy
bloków pominąć.
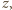 a dolny pozostanie nieruchomy, to ciężarek przesunie
się w górę o
a dolny pozostanie nieruchomy, to ciężarek przesunie
się w górę o
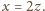 Przy tym sprężynka ulegnie skróceniu
o
Przy tym sprężynka ulegnie skróceniu
o
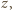 czyli siła wywierana przez nić
czyli siła wywierana przez nić
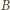 zmniejszy się o
zmniejszy się o
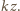 Siła napięcia nici
Siła napięcia nici
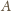 jest dwukrotnie mniejsza, zatem
zmniejszy się ona o
jest dwukrotnie mniejsza, zatem
zmniejszy się ona o
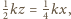 tak jakby ciężarek wisiał na
sprężynce o stałej sprężystości
tak jakby ciężarek wisiał na
sprężynce o stałej sprężystości
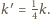 Szukany okres drgań jest
opisany wyrażeniem
Szukany okres drgań jest
opisany wyrażeniem
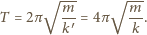
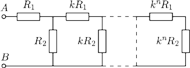
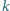 razy większy niż w poprzednim.
Znaleźć opór między punktami
razy większy niż w poprzednim.
Znaleźć opór między punktami
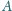 i
i
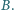 Opory w pierwszym
oczku sieci wynoszą
Opory w pierwszym
oczku sieci wynoszą
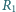 oraz
oraz
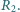
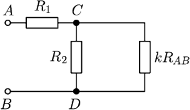
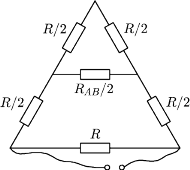
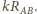 Zatem można przedstawić go
w postaci pokazanej na rysunku obok. Stąd wynika, że
Zatem można przedstawić go
w postaci pokazanej na rysunku obok. Stąd wynika, że
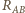 spełnia
równanie:
spełnia
równanie:
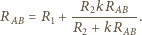
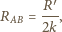

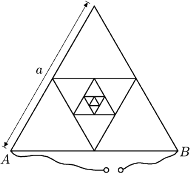
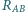 między punktami
między punktami
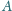 i
i
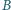 układu zbudowanego z cienkiej przewodzącej siatki. Przyjąć, że liczba
zmniejszających się oczek siatki jest bardzo duża. Długość boku trójkąta jest
równa
układu zbudowanego z cienkiej przewodzącej siatki. Przyjąć, że liczba
zmniejszających się oczek siatki jest bardzo duża. Długość boku trójkąta jest
równa
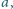 a gęstość liniowa drutu, z którego zrobiona jest siatka,
wynosi
a gęstość liniowa drutu, z którego zrobiona jest siatka,
wynosi
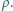
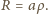 „Wewnętrzny”
układ składa się z nieskończonej ilości oczek, a jego opór wynosi
„Wewnętrzny”
układ składa się z nieskończonej ilości oczek, a jego opór wynosi
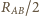 (z symetrii układu). Zatem
(z symetrii układu). Zatem
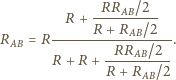
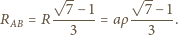
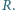 Odczytano wskazanie amperomierza
Odczytano wskazanie amperomierza
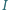 dla różnych
wartości
dla różnych
wartości
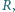 a wyniki przedstawiono w tabeli:
a wyniki przedstawiono w tabeli: 
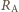 będzie szukanym oporem amperomierza, a
będzie szukanym oporem amperomierza, a
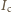 – natężeniem
prądu całkowitego, czyli sumą natężenia prądu płynącego przez
amperomierz
– natężeniem
prądu całkowitego, czyli sumą natężenia prądu płynącego przez
amperomierz
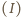 i przez bocznik. Napięcie na amperomierzu i boczniku
jest jednakowe, zatem
i przez bocznik. Napięcie na amperomierzu i boczniku
jest jednakowe, zatem
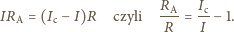
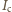 jest stałe, to wykres zależności
jest stałe, to wykres zależności
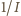 od
od
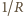 powinien
być liniowy, co dla danej serii pomiarów sprawdza się bardzo dobrze.
Z ekstrapolacji prostej do przecięcia z osią
powinien
być liniowy, co dla danej serii pomiarów sprawdza się bardzo dobrze.
Z ekstrapolacji prostej do przecięcia z osią
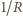 (tzn. do punktu,
w którym
(tzn. do punktu,
w którym
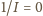 ) znajdujemy
) znajdujemy
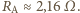
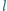 i masie
i masie
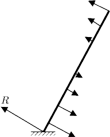
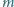 postawiono
pionowo na poziomym podłożu i zaczął się on przewracać bez poślizgu. Pręt
nie wygina się, a przy przekroczeniu w jakimkolwiek punkcie pewnej wartości
momentu siły zginającej
postawiono
pionowo na poziomym podłożu i zaczął się on przewracać bez poślizgu. Pręt
nie wygina się, a przy przekroczeniu w jakimkolwiek punkcie pewnej wartości
momentu siły zginającej
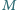 ulega złamaniu w tym punkcie. Obliczyć
minimalną wartość
ulega złamaniu w tym punkcie. Obliczyć
minimalną wartość
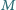 niezbędną do tego, aby pręt nie złamał się przed
upadkiem. W którym punkcie pręt się złamie, gdy
niezbędną do tego, aby pręt nie złamał się przed
upadkiem. W którym punkcie pręt się złamie, gdy
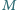 ma wartość
nieco mniejszą?
ma wartość
nieco mniejszą?
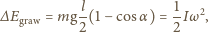
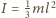 jest momentem bezwładności pręta względem punktu
podparcia, wyznaczamy prędkość kątową pręta
jest momentem bezwładności pręta względem punktu
podparcia, wyznaczamy prędkość kątową pręta
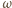 w zależności od
kąta odchylenia od pionu
w zależności od
kąta odchylenia od pionu
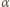 :
:
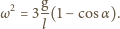
 :
:
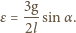
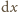 i masie
i masie
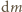 odległe od punktu podparcia o
odległe od punktu podparcia o
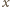 i dla każdego z nich
wyznaczmy „siłę wyginającą”
i dla każdego z nich
wyznaczmy „siłę wyginającą”
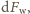 tzn. prostopadłą do pręta składową
siły wywieranej przez dany element na sąsiednie. Jeśli dodatni zwrot tej siły jest
w stronę spadku pręta, to jest ona równa różnicy prostopadłej składowej siły
ciężkości
tzn. prostopadłą do pręta składową
siły wywieranej przez dany element na sąsiednie. Jeśli dodatni zwrot tej siły jest
w stronę spadku pręta, to jest ona równa różnicy prostopadłej składowej siły
ciężkości
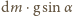 i iloczynu
i iloczynu
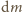 przez prostopadłą składową
przyspieszenia:
przez prostopadłą składową
przyspieszenia:
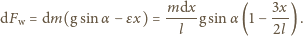
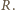 Moment
Moment
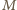 siły zginającej pręt
w punkcie
siły zginającej pręt
w punkcie
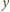 jest równy sumie momentów sił
jest równy sumie momentów sił
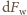 dla wszystkich
dla wszystkich
 większych od
większych od
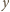 :
:
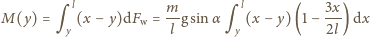
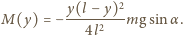
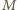 występuje tuż przed upadkiem
występuje tuż przed upadkiem
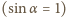 i w punkcie
i w punkcie
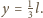 Wynosi ona
Wynosi ona
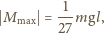
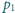 oraz bańka mydlana o promieniu
oraz bańka mydlana o promieniu
 . Napięcie
powierzchniowe błony mydlanej wynosi
. Napięcie
powierzchniowe błony mydlanej wynosi
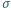 , temperatura układu
, temperatura układu
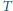 jest utrzymywana na stałym poziomie. Wyznaczyć ciśnienie
jest utrzymywana na stałym poziomie. Wyznaczyć ciśnienie
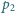 , do
którego należy sprężyć powietrze za pomocą tłoka, żeby promień bańki
zmniejszył się dwukrotnie.
, do
którego należy sprężyć powietrze za pomocą tłoka, żeby promień bańki
zmniejszył się dwukrotnie.
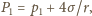 gdzie
gdzie
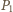 jest ciśnieniem wewnątrz bańki. Po zmniejszeniu promienia bańki
o połowę ciśnienie wywierane przez zakrzywioną powierzchnię bańki
zwiększy się do
jest ciśnieniem wewnątrz bańki. Po zmniejszeniu promienia bańki
o połowę ciśnienie wywierane przez zakrzywioną powierzchnię bańki
zwiększy się do
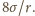 Skoro temperatura układu jest stała, to ciśnienie
powietrza wewnątrz bańki, odwrotnie proporcjonalne do jej objętości,
wzrośnie 8 razy,
Skoro temperatura układu jest stała, to ciśnienie
powietrza wewnątrz bańki, odwrotnie proporcjonalne do jej objętości,
wzrośnie 8 razy,
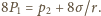 Z otrzymanych dwóch równań
wyznaczamy
Z otrzymanych dwóch równań
wyznaczamy
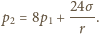
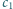 oraz
oraz
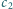 , których temperatury wynoszą, odpowiednio,
, których temperatury wynoszą, odpowiednio,
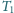 i
i
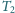 . Po usunięciu przegrody różnica początkowej
temperatury jednej z cieczy oraz ustanowionej temperatury równowagi okazała
się dwa razy mniejsza od początkowej różnicy temperatur cieczy. Znaleźć
stosunek mas cieczy
. Po usunięciu przegrody różnica początkowej
temperatury jednej z cieczy oraz ustanowionej temperatury równowagi okazała
się dwa razy mniejsza od początkowej różnicy temperatur cieczy. Znaleźć
stosunek mas cieczy
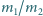 .
.
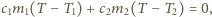 a stąd
a stąd
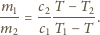
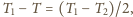 czyli
czyli
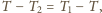 co ostatecznie daje:
co ostatecznie daje:
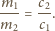
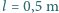 średnia pionowa odległość między atomami wynosi
średnia pionowa odległość między atomami wynosi
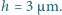
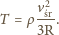
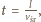 z drugiej jest to czas spadku
swobodnego równy
z drugiej jest to czas spadku
swobodnego równy
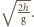 Stąd
Stąd
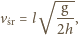
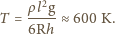
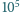 K umieszczono w polu
magnetycznym o indukcji 0,1 T. Znaleźć promień cyklotronowy
elektronów w tej plazmie.
K umieszczono w polu
magnetycznym o indukcji 0,1 T. Znaleźć promień cyklotronowy
elektronów w tej plazmie.
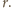 Siła wywierana przez pole magnetyczne
o indukcji
Siła wywierana przez pole magnetyczne
o indukcji
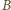 jest siłą dośrodkową:
jest siłą dośrodkową:
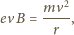
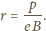
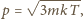 co daje ostatecznie
co daje ostatecznie
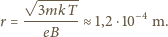
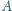 o temperaturze
o temperaturze
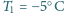 i oddaje ciepło otoczeniu o temperaturze
i oddaje ciepło otoczeniu o temperaturze
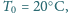 , działając na
następującej zasadzie. Naczynie o stałej objętości początkowo zawiera powietrze
atmosferyczne o temperaturze
, działając na
następującej zasadzie. Naczynie o stałej objętości początkowo zawiera powietrze
atmosferyczne o temperaturze
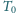 i ciśnieniu
i ciśnieniu
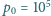 Pa,
następnie przy zachowaniu doskonałej izolacji termicznej pompa próżniowa
obniża ciśnienie w naczyniu do osiągnięcia temperatury
Pa,
następnie przy zachowaniu doskonałej izolacji termicznej pompa próżniowa
obniża ciśnienie w naczyniu do osiągnięcia temperatury
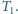 Dalej
odpompowuje się powietrze aż do stanu bliskiego próżni, przy czym
temperatura pozostaje równa
Dalej
odpompowuje się powietrze aż do stanu bliskiego próżni, przy czym
temperatura pozostaje równa
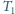 wskutek pobierania ciepła od
wskutek pobierania ciepła od
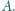 Następnie naczynie jest ponownie napełniane powietrzem atmosferycznym i cykl
się powtarza. Ile wynosi minimalna wartość pracy pompy niezbędnej do
odprowadzenia 1 J ciepła od
Następnie naczynie jest ponownie napełniane powietrzem atmosferycznym i cykl
się powtarza. Ile wynosi minimalna wartość pracy pompy niezbędnej do
odprowadzenia 1 J ciepła od
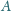 ?
?
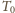 i tłok. Otwarcie zaworu łączącego cylinder z naczyniem następuje
w chwili dojścia tłoka „do końca” (objętość cylindra równa zeru),
po osiągnięciu przez tłok położenia przeciwnego następuje zamknięcie tego
zaworu, a po cofnięciu tłoka do położenia, w którym powietrze pobrane
z naczynia zostanie sprężone do ciśnienia
i tłok. Otwarcie zaworu łączącego cylinder z naczyniem następuje
w chwili dojścia tłoka „do końca” (objętość cylindra równa zeru),
po osiągnięciu przez tłok położenia przeciwnego następuje zamknięcie tego
zaworu, a po cofnięciu tłoka do położenia, w którym powietrze pobrane
z naczynia zostanie sprężone do ciśnienia
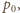 następuje otwarcie
zaworu umożliwiającego odprowadzenie na zewnątrz sprężonej partii gazu.
Ten zawór zostaje zamknięty tuż przed otwarciem pierwszego. Na każdy
cykl przemian w naczyniu próżniowym przypada wiele cykli pracy
pompy. Powietrze należy uważać za gaz doskonały o cieple molowym
następuje otwarcie
zaworu umożliwiającego odprowadzenie na zewnątrz sprężonej partii gazu.
Ten zawór zostaje zamknięty tuż przed otwarciem pierwszego. Na każdy
cykl przemian w naczyniu próżniowym przypada wiele cykli pracy
pompy. Powietrze należy uważać za gaz doskonały o cieple molowym
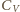 równym (5/2)R.
równym (5/2)R.
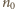 i
i
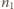 początkową liczbę moli
powietrza w naczyniu oraz liczbę moli w chwili osiągnięcia temperatury
początkową liczbę moli
powietrza w naczyniu oraz liczbę moli w chwili osiągnięcia temperatury
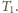 Z równania adiabaty w zmiennych
Z równania adiabaty w zmiennych
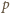 –
–
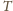
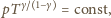
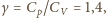 po przekształceniach znajdujemy
po przekształceniach znajdujemy
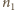

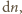 przy założeniu, że ciśnienie w naczyniu
pozostaje w przybliżeniu stałe i równe
przy założeniu, że ciśnienie w naczyniu
pozostaje w przybliżeniu stałe i równe
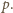 Jeśli objętość
cylindra pompy jest równa
Jeśli objętość
cylindra pompy jest równa
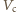 (zgodnie z podanym założeniem
(zgodnie z podanym założeniem
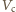 jest znacznie mniejsze od objętości naczynia), to wejdzie do niego
jest znacznie mniejsze od objętości naczynia), to wejdzie do niego
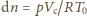 moli powietrza, a praca przeciw sile parcia z zewnątrz
wyniesie
moli powietrza, a praca przeciw sile parcia z zewnątrz
wyniesie
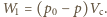 Sprężanie powietrza w cylindrze zachodzi
izotermicznie, zatem praca
Sprężanie powietrza w cylindrze zachodzi
izotermicznie, zatem praca
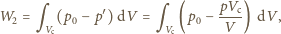
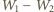 i okazuje się równa
i okazuje się równa
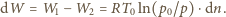
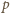 zależy od liczby moli
zależy od liczby moli
 pozostałej w naczyniu wg równania
pozostałej w naczyniu wg równania
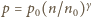 i w wyniku
całkowania otrzymujemy
i w wyniku
całkowania otrzymujemy
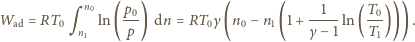
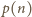 ma postać
ma postać
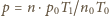 i całkowanie daje wynik
i całkowanie daje wynik
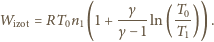
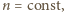
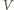 jest
zmienną) ciepło to jest równe
jest
zmienną) ciepło to jest równe
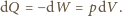
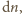 która jest równoważna
która jest równoważna
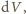 o ile
o ile
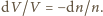 Dlatego
Dlatego
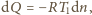 a jeśli stanem
końcowym jest próżnia, to
a jeśli stanem
końcowym jest próżnia, to
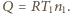 Szukany iloraz
Szukany iloraz
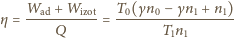
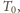
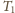 i
i
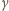 przyjmuje wartość 1,48, co można
porównać z
przyjmuje wartość 1,48, co można
porównać z
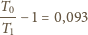
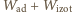 ), to wartość
), to wartość
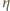 zmalałaby do 0,109.
zmalałaby do 0,109.

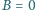 ). Oporności oporników są jednakowe, jednakowe są także
trzy pola powierzchni objęte oczkami obwodu: między linią przerywaną
a środkowym woltomierzem, między środkowym woltomierzem a dolnym
opornikiem oraz między dolnym opornikiem a dolnym woltomierzem.
Jeśli dolny woltomierz wskazuje 1 V, to jakie jest wskazanie pozostałych
woltomierzy?
). Oporności oporników są jednakowe, jednakowe są także
trzy pola powierzchni objęte oczkami obwodu: między linią przerywaną
a środkowym woltomierzem, między środkowym woltomierzem a dolnym
opornikiem oraz między dolnym opornikiem a dolnym woltomierzem.
Jeśli dolny woltomierz wskazuje 1 V, to jakie jest wskazanie pozostałych
woltomierzy?
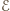 i przyjmijmy, że ma ona zwrot prawoskrętny – oczywiście wtedy
prąd płynie przez oba oporniki prawoskrętnie. Napięcia na woltomierzach
i przyjmijmy, że ma ona zwrot prawoskrętny – oczywiście wtedy
prąd płynie przez oba oporniki prawoskrętnie. Napięcia na woltomierzach
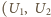 i
i
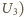 niech będą dodatnie, gdy plus jest po prawej stronie.
Dla kolejnych oczek obowiązują równania
niech będą dodatnie, gdy plus jest po prawej stronie.
Dla kolejnych oczek obowiązują równania

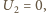
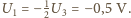
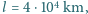 promień Ziemi
promień Ziemi
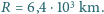 Przyjąć, że przyspieszenie swobodnego spadku na powierzchni Ziemi wynosi
Przyjąć, że przyspieszenie swobodnego spadku na powierzchni Ziemi wynosi
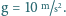
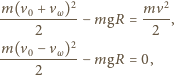
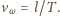 Stąd otrzymujemy:
Stąd otrzymujemy:
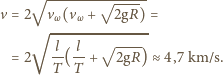
 . Z jaką
minimalną prędkością powinien poruszać się w poziomej części
kawałek sznurka o długości
. Z jaką
minimalną prędkością powinien poruszać się w poziomej części
kawałek sznurka o długości
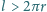 , tak aby przejść przez
pętlę? Założyć, że promień pętli jest dużo większy od promieni rurki
i sznurka.
, tak aby przejść przez
pętlę? Założyć, że promień pętli jest dużo większy od promieni rurki
i sznurka.
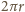 i masie
i masie
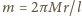 zostaje podniesiony
na wysokość
zostaje podniesiony
na wysokość
 :
:
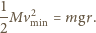
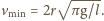
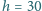 cm, a gęstość zmienia
się liniowo z wysokością od
cm, a gęstość zmienia
się liniowo z wysokością od
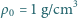 przy powierzchni do
przy powierzchni do
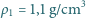 przy dnie. W połowie głębokości naczynia pływa
w stanie równowagi nurek Kartezjusza – niewielka probówka ze szkła
o gęstości
przy dnie. W połowie głębokości naczynia pływa
w stanie równowagi nurek Kartezjusza – niewielka probówka ze szkła
o gęstości
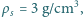 zawierająca pewną ilość powietrza
i otwarta od dołu. Czy ten stan równowagi jest trwały ze względu na
małe przesunięcia pionowe nurka? Ciśnienie atmosferyczne wynosi
zawierająca pewną ilość powietrza
i otwarta od dołu. Czy ten stan równowagi jest trwały ze względu na
małe przesunięcia pionowe nurka? Ciśnienie atmosferyczne wynosi
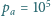 Pa.
Pa.
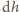 w górę powoduje spadek
siły wyporu o wielkość
w górę powoduje spadek
siły wyporu o wielkość
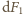 wynikającą ze spadku gęstości
wody
wynikającą ze spadku gęstości
wody
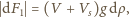
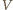 jest objętością powietrza w nurku,
jest objętością powietrza w nurku,
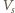 – objętością
szkła, a
– objętością
szkła, a
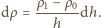 Z drugiej strony, nastąpi wtedy wzrost siły
wyporu o wielkość
Z drugiej strony, nastąpi wtedy wzrost siły
wyporu o wielkość
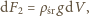
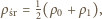 a
a
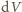 jest wzrostem objętości, będącym
skutkiem spadku ciśnienia i rozprężenia powietrza w nurku. Warunkiem
równowagi trwałej jest
jest wzrostem objętości, będącym
skutkiem spadku ciśnienia i rozprężenia powietrza w nurku. Warunkiem
równowagi trwałej jest
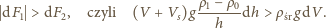
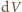 na podstawie prawa przemiany izotermicznej, gdyż
powietrza w nurku jest niewiele i kontakt ze ściankami zapewnia stałość
temperatury. Zatem
na podstawie prawa przemiany izotermicznej, gdyż
powietrza w nurku jest niewiele i kontakt ze ściankami zapewnia stałość
temperatury. Zatem
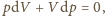 albo
albo
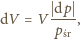
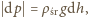 a
a
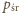 jest ciśnieniem w położeniu
równowagi nurka, czyli sumą ciśnienia atmosferycznego i ciśnienia górnej
połowy słupa wody. Średnia gęstość wody w górnej połowie wynosi
jest ciśnieniem w położeniu
równowagi nurka, czyli sumą ciśnienia atmosferycznego i ciśnienia górnej
połowy słupa wody. Średnia gęstość wody w górnej połowie wynosi
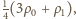 zatem
zatem
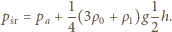
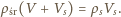
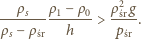
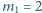 kg, poruszająca się z prędkością początkową
kg, poruszająca się z prędkością początkową
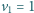 m/s, zderzyła się centralnie i doskonale sprężyście z kulą
o masie
m/s, zderzyła się centralnie i doskonale sprężyście z kulą
o masie
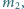 początkowo spoczywającą. Druga kula zderzyła się
w podobny sposób z trzecią kulą o masie
początkowo spoczywającą. Druga kula zderzyła się
w podobny sposób z trzecią kulą o masie
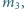 ta z kolei z czwartą,
czwarta z piątą itd. aż do kuli o numerze 2011. Dana jest masa ostatniej
kuli
ta z kolei z czwartą,
czwarta z piątą itd. aż do kuli o numerze 2011. Dana jest masa ostatniej
kuli
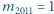 kg. Dobrać masy pośrednie tak, aby ostatnia kula
uzyskała największą prędkość, przy ustalonych wartościach
kg. Dobrać masy pośrednie tak, aby ostatnia kula
uzyskała największą prędkość, przy ustalonych wartościach
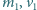 i
i
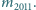 Ile wynosi ta największa prędkość? Pominąć efekty związane
z obrotem kul.
Ile wynosi ta największa prędkość? Pominąć efekty związane
z obrotem kul.
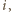
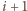 oraz
oraz
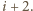 Z zasad zachowania energii i pędu oraz warunku zerowej
prędkości początkowej kul
Z zasad zachowania energii i pędu oraz warunku zerowej
prędkości początkowej kul
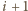 i
i
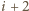 wyprowadzamy
standardowe wzory
wyprowadzamy
standardowe wzory
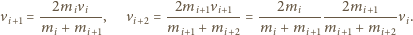
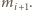 Nietrudno sprawdzić, że jest ono osiągane dla
Nietrudno sprawdzić, że jest ono osiągane dla
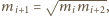 tzn. masy powinny tworzyć ciąg geometryczny.
Ilorazem tego ciągu jest
tzn. masy powinny tworzyć ciąg geometryczny.
Ilorazem tego ciągu jest
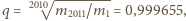 natomiast
prędkości tworzą ciąg o ilorazie
natomiast
prędkości tworzą ciąg o ilorazie
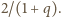 Zatem
Zatem
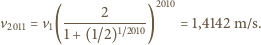
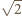 m/s.
Energia kinetyczna ostatniej kuli jest więc prawie dokładnie równa początkowej
energii kinetycznej (po zderzeniach z kulą poprzednią i następną każda z kul
pozostaje prawie nieruchoma).
m/s.
Energia kinetyczna ostatniej kuli jest więc prawie dokładnie równa początkowej
energii kinetycznej (po zderzeniach z kulą poprzednią i następną każda z kul
pozostaje prawie nieruchoma).
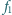 i
i
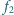 są
odległe o
są
odległe o
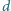 i wykonane z tego samego szkła. Jaki warunek muszą
spełniać podane parametry, aby ogniskowa zespołu nie zależała od długości
fali (aby układ był achromatyczny)? Zmiany współczynnika załamania
są niewielkie.
i wykonane z tego samego szkła. Jaki warunek muszą
spełniać podane parametry, aby ogniskowa zespołu nie zależała od długości
fali (aby układ był achromatyczny)? Zmiany współczynnika załamania
są niewielkie.
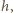 a wychodząc z układu przecina oś pod kątem
a wychodząc z układu przecina oś pod kątem
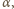 to ogniskowa wynosi
to ogniskowa wynosi
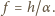
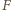 układu jest dość standardowe i nie będziemy
go powtarzać. Otrzymuje się
układu jest dość standardowe i nie będziemy
go powtarzać. Otrzymuje się
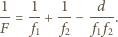
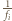 w postaci
w postaci
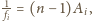 gdzie
gdzie
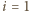 lub 2,
lub 2,
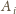 nie zależy od
nie zależy od
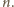 Przy niewielkiej zmianie
Przy niewielkiej zmianie
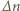 zmiana
zdolności skupiającej układu
zmiana
zdolności skupiającej układu
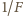 wynosi
wynosi
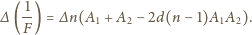
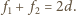
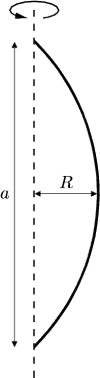
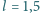 m i masie
m i masie
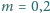 kg (jednorodnie
rozłożonej) jest zamocowana końcami w dwóch punktach odległych o
kg (jednorodnie
rozłożonej) jest zamocowana końcami w dwóch punktach odległych o
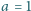 m (
m (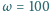 rad/s i względem tego
obracającego się układu odniesienia pozostaje nieruchoma. Pomijając efekty siły
ciężkości, obliczyć numerycznie odległość
rad/s i względem tego
obracającego się układu odniesienia pozostaje nieruchoma. Pomijając efekty siły
ciężkości, obliczyć numerycznie odległość
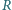 środkowego punktu
linki od osi obrotu.
środkowego punktu
linki od osi obrotu.
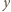 będzie współrzędną wzdłuż osi obrotu, natomiast
będzie współrzędną wzdłuż osi obrotu, natomiast
 – współrzędną wzdłuż osi prostopadłej. Składowa
– współrzędną wzdłuż osi prostopadłej. Składowa
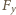 siły
napięcia linki jest stała, natomiast przyrost składowej
siły
napięcia linki jest stała, natomiast przyrost składowej
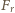 równoważy siłę
odśrodkową działającą na fragment linki o długości
równoważy siłę
odśrodkową działającą na fragment linki o długości
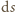 i masie
i masie
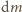 :
:
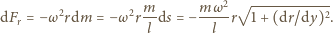
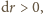
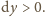 Kierunek
siły napięcia jest styczny do linki, czyli
Kierunek
siły napięcia jest styczny do linki, czyli
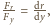 a stąd
a stąd
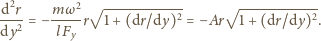
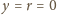 i dowolnie
wybranych wartości
i dowolnie
wybranych wartości
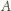 oraz
oraz
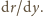 Wartości te należy dobrać
tak, aby w punkcie
Wartości te należy dobrać
tak, aby w punkcie
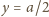 osiągnąć
osiągnąć
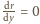 oraz długość linki
równą
oraz długość linki
równą
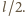 Okazuje się, że przy danych
Okazuje się, że przy danych
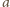 i
i
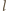 właściwymi
wyborami są
właściwymi
wyborami są
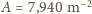 (faktycznie wyznaczamy w ten sposób
(faktycznie wyznaczamy w ten sposób
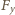 ; wartości
; wartości
 i
i
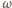 nie wpływają na kształt linki) oraz
nie wpływają na kształt linki) oraz
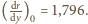 Maksymalną wartością
Maksymalną wartością
 jest
jest
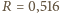 m.
Dla porównania, dla krzywej łańcuchowej (cosinusa hiperbolicznego) byłoby
m.
Dla porównania, dla krzywej łańcuchowej (cosinusa hiperbolicznego) byłoby
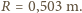
 wykonano niewielki otworek o promieniu
wykonano niewielki otworek o promieniu
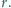 Wzdłuż osi
otworka rozchodzi się cienki promień światła. Jaki musi być poziom cieczy
Wzdłuż osi
otworka rozchodzi się cienki promień światła. Jaki musi być poziom cieczy
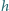 nad otworkiem, aby promień mógł wyjść ze strugi cieczy, ani razu
nie dokonując całkowicie wewnętrznego odbicia? Założyć, że współczynnik
załamania
nad otworkiem, aby promień mógł wyjść ze strugi cieczy, ani razu
nie dokonując całkowicie wewnętrznego odbicia? Założyć, że współczynnik
załamania
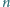 cieczy jest dostatecznie duży. Pominąć zmianę przekroju
poprzecznego cieczy.
cieczy jest dostatecznie duży. Pominąć zmianę przekroju
poprzecznego cieczy.
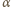 z poziomym
promieniem światła. Z drugiej strony kąt ten jest wyznaczony przez stosunek
składowej poziomej i pionowej cieczy:
z poziomym
promieniem światła. Z drugiej strony kąt ten jest wyznaczony przez stosunek
składowej poziomej i pionowej cieczy:
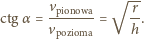
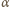 jest kątem granicznym, jeśli
jest kątem granicznym, jeśli
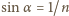 , zatem:
, zatem:
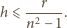
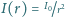 .
Jak zmienia się ta zależność, gdy w powietrzu znajduje się pochłaniający
światło pył o koncentracji
.
Jak zmienia się ta zależność, gdy w powietrzu znajduje się pochłaniający
światło pył o koncentracji
 i polu powierzchni drobiny
i polu powierzchni drobiny
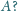
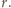 Kulę
dzielimy za pomocą współśrodkowych sfer na
Kulę
dzielimy za pomocą współśrodkowych sfer na
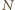 części o jednakowej
grubości
części o jednakowej
grubości
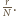 W
W
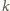 -tej części, licząc od środka, znajduje się
-tej części, licząc od środka, znajduje się
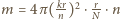 drobin pyłu, które zasłaniają powierzchnię
drobin pyłu, które zasłaniają powierzchnię
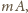 czyli
czyli
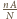 całości powierzchni sfery. Drobiny w różnych warstwach
ustawione są przypadkowo i niezależnie od siebie, więc całkowita niezasłonięta
powierzchnia to
całości powierzchni sfery. Drobiny w różnych warstwach
ustawione są przypadkowo i niezależnie od siebie, więc całkowita niezasłonięta
powierzchnia to
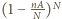 całej sfery, co po przejściu do granicy
całej sfery, co po przejściu do granicy
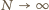 daje
daje
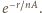 Po podzieleniu na jednostkę powierzchni
otrzymujemy
Po podzieleniu na jednostkę powierzchni
otrzymujemy
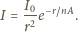
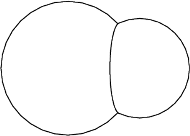
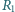 i
i
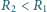 są
połączone tak, jak na rysunku. Jaki promień krzywizny ma błonka oddzielająca
bańki?
są
połączone tak, jak na rysunku. Jaki promień krzywizny ma błonka oddzielająca
bańki?
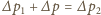 , czyli
, czyli
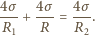
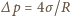 , ponieważ błonka ma dwie powierzchnie: zewnętrzną
i wewnętrzną. Zatem
, ponieważ błonka ma dwie powierzchnie: zewnętrzną
i wewnętrzną. Zatem
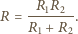
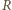 . Powierzchnia tego koła wynosi
. Powierzchnia tego koła wynosi
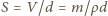 . Siła przyciągania między płytkami równa jest
. Siła przyciągania między płytkami równa jest
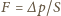 , gdzie
, gdzie
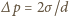 jest ciśnieniem wywieranym przez
zakrzywioną powierzchnię cieczy. Ostatecznie
jest ciśnieniem wywieranym przez
zakrzywioną powierzchnię cieczy. Ostatecznie
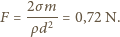
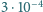 A i zakresie
A i zakresie
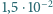 A,
wyposażony w opornik wewnętrzny
A,
wyposażony w opornik wewnętrzny
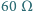 , należy przekształcić
w miernik uniwersalny (amperomierz o zakresach 100 mA i 5 A oraz
woltomierz 10 V, 100 V i 1000 V). Zaproponować schemat połączeń
i obliczyć parametry niezbędnych oporników.
, należy przekształcić
w miernik uniwersalny (amperomierz o zakresach 100 mA i 5 A oraz
woltomierz 10 V, 100 V i 1000 V). Zaproponować schemat połączeń
i obliczyć parametry niezbędnych oporników.
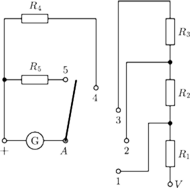
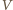 , a dla położeń 4 i 5 jako amperomierz o zaciskach
„+” i
, a dla położeń 4 i 5 jako amperomierz o zaciskach
„+” i
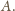
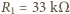 ,
,
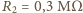 ,
,
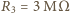 ,
,
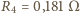 ,
,
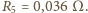
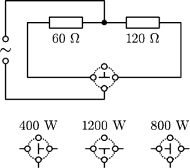
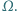 Zaprojektować schemat
połączeń pozwalających użytkować kuchenkę w trzech zakresach mocy: 400,
800 i 1200 W.
Zaprojektować schemat
połączeń pozwalających użytkować kuchenkę w trzech zakresach mocy: 400,
800 i 1200 W.
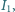 a w ramce
leżącej w płaszczyźnie prostopadłej do tego przewodnika – prąd o natężeniu
a w ramce
leżącej w płaszczyźnie prostopadłej do tego przewodnika – prąd o natężeniu
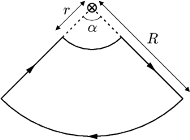
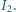 Ramka składa się z dwóch odcinków radialnych o kącie rozwarcia
Ramka składa się z dwóch odcinków radialnych o kącie rozwarcia
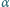 oraz łuków okręgów odległych od przewodnika prostoliniowego o
oraz łuków okręgów odległych od przewodnika prostoliniowego o
 i
i
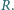 Względna przenikalność magnetyczna ośrodka jest
równa 1. Znaleźć siłę i moment siły oddziaływania ramki na przewodnik
prostoliniowy.
Względna przenikalność magnetyczna ośrodka jest
równa 1. Znaleźć siłę i moment siły oddziaływania ramki na przewodnik
prostoliniowy.
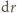 działa siła
działa siła
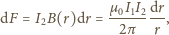
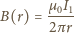
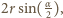 stąd moment pary sił
wynosi
stąd moment pary sił
wynosi
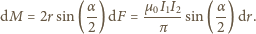
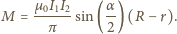
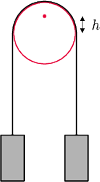
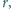 który może się swobodnie
obracać wokół osi odległej o
który może się swobodnie
obracać wokół osi odległej o
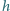 od środka krążka. Nić nie ślizga
się po krążku. Obliczyć okres małych drgań układu wokół położenia
równowagi.
od środka krążka. Nić nie ślizga
się po krążku. Obliczyć okres małych drgań układu wokół położenia
równowagi.
 oznacza podniesienie jego środka
o
oznacza podniesienie jego środka
o
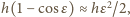 a zatem podniesienie środka masy ciężarków
o tę samą wielkość. Łączna energia potencjalna ciężarków wzrośnie o
a zatem podniesienie środka masy ciężarków
o tę samą wielkość. Łączna energia potencjalna ciężarków wzrośnie o
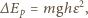
 jest masą jednego ciężarka. Prędkość ciężarków
jest masą jednego ciężarka. Prędkość ciężarków
 wystarczy wyznaczyć w pierwszym rzędzie względem prędkości
kątowej krążka
wystarczy wyznaczyć w pierwszym rzędzie względem prędkości
kątowej krążka
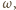 ponieważ do energii kinetycznej wchodzi ona
w kwadracie. Ze względu na długość nici ruch ciężarków odbywa się
wzdłuż osi pionowej i widzimy, że w tym przybliżeniu
ponieważ do energii kinetycznej wchodzi ona
w kwadracie. Ze względu na długość nici ruch ciężarków odbywa się
wzdłuż osi pionowej i widzimy, że w tym przybliżeniu
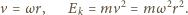
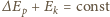 znajdujemy
znajdujemy