Klub 44F - zadania VI 2005»Zadanie 392
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania VI 2005
- Publikacja w Delcie: czerwiec 2005
- Publikacja elektroniczna: 24 sierpnia 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (76 KB)

Izolowany termicznie cylinder jest podzielony nieprzewodzącym ciepła tłokiem na dwie równe części zawierające jednakowe ilości tego samego gazu o temperaturze 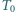 pod ciśnieniem
pod ciśnieniem 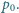 Do wnętrza doprowadzamy pewną ustaloną ilość ciepła
Do wnętrza doprowadzamy pewną ustaloną ilość ciepła 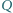 (np. grzałką elektryczną). W którym przypadku ciśnienie wzrośnie bardziej: gdy całe ciepło dostarczymy do jednej części cylindra, czy gdy do każdej części dostarczymy połowę?
(np. grzałką elektryczną). W którym przypadku ciśnienie wzrośnie bardziej: gdy całe ciepło dostarczymy do jednej części cylindra, czy gdy do każdej części dostarczymy połowę?
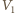 i
i 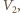 ich temperatury przez
ich temperatury przez 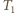 i
i 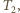 ciśnienie (jednakowe) przez
ciśnienie (jednakowe) przez 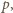 a liczbę moli w każdej z części przez
a liczbę moli w każdej z części przez 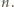 Spełnione są równania
Spełnione są równania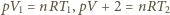
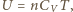 a przyrost całkowitej energii wewnętrznej w każdym z rozpatrywanych przypadków jest równy
a przyrost całkowitej energii wewnętrznej w każdym z rozpatrywanych przypadków jest równy 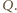 Stąd
Stąd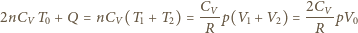
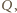 czyli wzrost ciśnienia nie zależy od tego podziału. (Dość podobne były przed wieloma laty zadania 198 i 257.)
czyli wzrost ciśnienia nie zależy od tego podziału. (Dość podobne były przed wieloma laty zadania 198 i 257.)
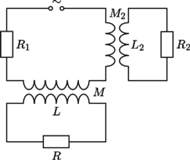
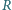 ) jest dołączony do źródła napięcia przemiennego przez transformator o indukcyjności uzwojenia wtórnego
) jest dołączony do źródła napięcia przemiennego przez transformator o indukcyjności uzwojenia wtórnego 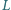 i współczynniku indukcji wzajemnej między uzwojeniami
i współczynniku indukcji wzajemnej między uzwojeniami 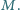 Ponadto w obwodzie występuje opornik
Ponadto w obwodzie występuje opornik 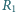 odpowiadający oporności przewodów i uzwojenia transformatora oraz drugi transformator opisany parametrami
odpowiadający oporności przewodów i uzwojenia transformatora oraz drugi transformator opisany parametrami 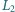 i
i 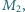 do którego dołączony jest opornik
do którego dołączony jest opornik 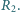 Ten drugi obwód symbolizuje prądy wirowe wzbudzane w przewodnikach, które przypadkiem znajdą się w pobliżu kabli doprowadzających energię do właściwego odbiornika.
Ten drugi obwód symbolizuje prądy wirowe wzbudzane w przewodnikach, które przypadkiem znajdą się w pobliżu kabli doprowadzających energię do właściwego odbiornika.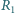 i
i 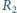 ) do mocy dostarczanej do opornika
) do mocy dostarczanej do opornika 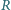 osiągał minimum dla pewnej częstotliwości?
osiągał minimum dla pewnej częstotliwości?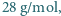 21% tlenu
21% tlenu 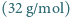 i 1% argonu
i 1% argonu 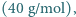 znaleźć prawdopodobieństwo fluktuacji gęstości tych gazów na poziomie większym niż 1% (dla objętości rozpatrywanych w przykładzie zilustrowanym tabelką w poniższej uwadze).
znaleźć prawdopodobieństwo fluktuacji gęstości tych gazów na poziomie większym niż 1% (dla objętości rozpatrywanych w przykładzie zilustrowanym tabelką w poniższej uwadze).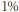 zależy bardzo silnie od promienia
zależy bardzo silnie od promienia  kuli, co widać z przytoczonej tabelki:
kuli, co widać z przytoczonej tabelki:![|-------|------|-------|-------|--------|-------| |r-[cm]--|--1---|5⋅10−5-|3⋅10−5-|2,5-⋅10−5|1-⋅10−5-| |θ [sek] |101014 | 1068 | 106 | 1 | 10−11 | -------------------------------------------------](/math/temat/fizyka/fizyka_statystyczna/zadania/2017/08/19/zf-466/3x-cee258ad6f163cb2712edf33b3db7796fca90dc8-dm-66,57,43-FF,FF,FF.gif)
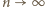 rozkład Poissona przechodzi na rozkład Gaussa (można to sprawdzić korzystając najpierw ze wzoru Stirlinga, a następnie z rozwinięcia logarytmu w szereg z dokładnością do dwóch wyrazów), mamy
rozkład Poissona przechodzi na rozkład Gaussa (można to sprawdzić korzystając najpierw ze wzoru Stirlinga, a następnie z rozwinięcia logarytmu w szereg z dokładnością do dwóch wyrazów), mamy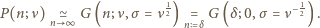
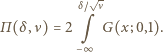
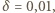 pozostaje więc tylko obliczenie
pozostaje więc tylko obliczenie 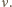 W tym celu obliczamy liczbę molekuł gazu w najmniejszej z rozpatrywanych objętości
W tym celu obliczamy liczbę molekuł gazu w najmniejszej z rozpatrywanych objętości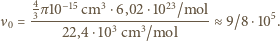


 oznacza średnią liczbę cząsteczek w małej objętości
oznacza średnią liczbę cząsteczek w małej objętości 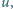 a
a 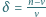 nazywane jest zagęszczeniem liczby cząsteczek w objętości
nazywane jest zagęszczeniem liczby cząsteczek w objętości 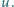 (Zakładamy, że w naczyniu o objętości
(Zakładamy, że w naczyniu o objętości 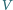 znajduje się
znajduje się  cząsteczek.)
cząsteczek.)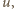 będącej częścią dużo większej objętości
będącej częścią dużo większej objętości 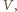 jest proporcjonalne do
jest proporcjonalne do 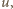 otrzymujemy, że liczba cząsteczek w objętości
otrzymujemy, że liczba cząsteczek w objętości  podlega statystyce Poissona
podlega statystyce Poissona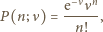
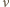 jest średnią liczbą cząsteczek w objętości
jest średnią liczbą cząsteczek w objętości 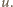 Wiedząc, że wariancja rozkładu Poissona
Wiedząc, że wariancja rozkładu Poissona 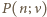 wynosi
wynosi 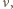 dostajemy
dostajemy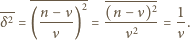
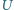 ze źródła zasilania, a do pozostałych dwóch dołączamy woltomierz o bardzo wielkim oporze własnym i mierzymy napięcie
ze źródła zasilania, a do pozostałych dwóch dołączamy woltomierz o bardzo wielkim oporze własnym i mierzymy napięcie 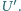 Istnieje sześć możliwych sposobów przyłączenia zasilania i woltomierza do "czarnej skrzynki", a zatem sześć możliwych wartości
Istnieje sześć możliwych sposobów przyłączenia zasilania i woltomierza do "czarnej skrzynki", a zatem sześć możliwych wartości 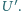 Zaprojektować taki możliwie najprostszy schemat "czarnej skrzynki", aby wśród nich znalazły się
Zaprojektować taki możliwie najprostszy schemat "czarnej skrzynki", aby wśród nich znalazły się 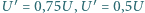 i
i 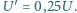
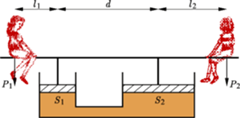
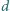 i połączonych z tłokami o powierzchniach
i połączonych z tłokami o powierzchniach 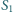 i
i 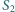 wywierającymi parcie na ciecz; odległości dziewczynek od punktów podparcia wynoszą odpowiednio
wywierającymi parcie na ciecz; odległości dziewczynek od punktów podparcia wynoszą odpowiednio 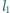 i
i 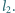 Jaki warunek muszą spełniać wymienione parametry oraz ciężary dziewczynek
Jaki warunek muszą spełniać wymienione parametry oraz ciężary dziewczynek 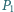 i
i 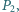 aby huśtawka pozostawała w równowadze? Ciężar huśtawki i tłoków pominąć.
aby huśtawka pozostawała w równowadze? Ciężar huśtawki i tłoków pominąć.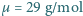 . Skorzystać z informacji, że satelita krążący wokół Ziemi na wysokości 100 km praktycznie nie napotyka oporu powietrza.
. Skorzystać z informacji, że satelita krążący wokół Ziemi na wysokości 100 km praktycznie nie napotyka oporu powietrza.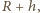 gdzie
gdzie 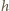 - wysokość 100 km, na której praktycznie nie występuje opór powietrza. Obliczmy, jak zmienia się przyspieszenie ziemskie w tak określonych granicach atmosfery:
- wysokość 100 km, na której praktycznie nie występuje opór powietrza. Obliczmy, jak zmienia się przyspieszenie ziemskie w tak określonych granicach atmosfery: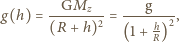
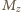 - masa Ziemi,
- masa Ziemi, 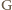 - stała grawitacji,
- stała grawitacji, 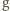 - przyspieszenie ziemskie na powierzchni Ziemi. Korzystając z tego, że
- przyspieszenie ziemskie na powierzchni Ziemi. Korzystając z tego, że 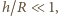 możemy przyjąć, że w pierwszym przybliżeniu
możemy przyjąć, że w pierwszym przybliżeniu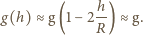
 i mającego podstawę jednostkową wynosi
i mającego podstawę jednostkową wynosi 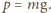 Całkowitą masę atmosfery
Całkowitą masę atmosfery 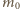 znajdujemy, mnożąc
znajdujemy, mnożąc  przez powierzchnię Ziemi:
przez powierzchnię Ziemi: 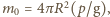 a stąd znajdujemy liczbę zawartych w atmosferze cząsteczek powietrza
a stąd znajdujemy liczbę zawartych w atmosferze cząsteczek powietrza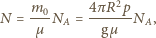
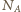 - liczba Avogadro. Podstawiając dane liczbowe, otrzymujemy
- liczba Avogadro. Podstawiając dane liczbowe, otrzymujemy 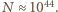
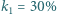 padającej na niego wiązki niespolaryzowanego światła, a dwa takie polaryzatory, ustawione jeden za drugim, przepuszczają
padającej na niego wiązki niespolaryzowanego światła, a dwa takie polaryzatory, ustawione jeden za drugim, przepuszczają 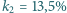 światła. Ile wynosi kąt
światła. Ile wynosi kąt  między płaszczyznami polaryzacji tych polaryzatorów?
między płaszczyznami polaryzacji tych polaryzatorów?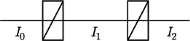
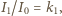 gdzie
gdzie 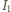 i
i 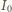 - natężenia wiązki padającej i przechodzącej dla pierwszego polaryzatora.
- natężenia wiązki padającej i przechodzącej dla pierwszego polaryzatora.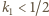 oznacza, że polaryzator częściowo pochłania światło. Jeżeli przepuszcza on, ze względu na pochłanianie, tylko
oznacza, że polaryzator częściowo pochłania światło. Jeżeli przepuszcza on, ze względu na pochłanianie, tylko 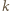 procent padającej wiązki, to
procent padającej wiązki, to 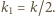 Gdy światło przechodzi przez dwa polaryzatory, to
Gdy światło przechodzi przez dwa polaryzatory, to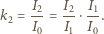
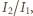 skorzystamy z prawa Malusa, które mówi, że natężenia światła spolaryzowanego padającego na polaryzator
skorzystamy z prawa Malusa, które mówi, że natężenia światła spolaryzowanego padającego na polaryzator 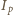 i z niego wychodzącego
i z niego wychodzącego 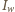 związane są wzorem
związane są wzorem 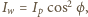 gdzie
gdzie 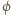 jest kątem między płaszczyzną polaryzacji światła padającego i płaszczyzną polaryzacji polaryzatora. Dodatkowo musimy uwzględnić to, że także w drugim polaryzatorze światło jest pochłaniane. Mamy więc:
jest kątem między płaszczyzną polaryzacji światła padającego i płaszczyzną polaryzacji polaryzatora. Dodatkowo musimy uwzględnić to, że także w drugim polaryzatorze światło jest pochłaniane. Mamy więc: 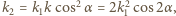 a stąd
a stąd 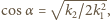 co daje
co daje 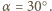
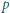 tego gazu w temperaturze
tego gazu w temperaturze 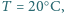 aby izolacja cieplna była skuteczna, jeżeli gazem jest azot, a odległość między podwójnymi ściankami termosu wynosi
aby izolacja cieplna była skuteczna, jeżeli gazem jest azot, a odległość między podwójnymi ściankami termosu wynosi 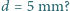 Średnica
Średnica  cząsteczki azotu wynosi około
cząsteczki azotu wynosi około 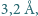 stała Avogadro
stała Avogadro 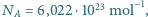 stała gazowa
stała gazowa 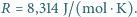
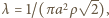 gdzie
gdzie 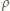 oznacza liczbę cząsteczek gazu w jednostce objętości.
oznacza liczbę cząsteczek gazu w jednostce objętości.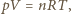 gdzie
gdzie 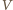 oznacza objętość gazu,
oznacza objętość gazu,  liczbę moli gazu, a
liczbę moli gazu, a 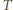 temperaturę w skali Kelvina. Liczba cząsteczek gazu w jednostce objętości
temperaturę w skali Kelvina. Liczba cząsteczek gazu w jednostce objętości 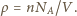 Korzystając z równania stanu oraz warunku
Korzystając z równania stanu oraz warunku 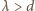 otrzymujemy:
otrzymujemy: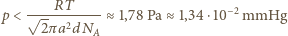
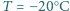 zderzają się. Ile, co najmniej, musiałaby wynosić prędkość każdej z kostek, aby w wyniku tego zderzenia kostki w całości wyparowały? Przyjmij, że w przybliżeniu ciepło właściwe lodu
zderzają się. Ile, co najmniej, musiałaby wynosić prędkość każdej z kostek, aby w wyniku tego zderzenia kostki w całości wyparowały? Przyjmij, że w przybliżeniu ciepło właściwe lodu 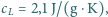 ciepło właściwe wody
ciepło właściwe wody 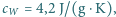 ciepło topnienia lodu
ciepło topnienia lodu 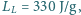 ciepło parowania wody
ciepło parowania wody 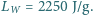
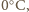 stopnienie lodu, podgrzanie wody do
stopnienie lodu, podgrzanie wody do 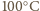 i odparowanie wody:
i odparowanie wody: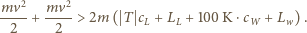
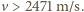
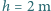 wydzielają się pęcherzyki gazu o średnicy
wydzielają się pęcherzyki gazu o średnicy 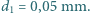 Jaka będzie średnica
Jaka będzie średnica 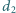 tych pęcherzyków, gdy osiągną one powierzchnię wody? Napięcie powierzchniowe wody wynosi
tych pęcherzyków, gdy osiągną one powierzchnię wody? Napięcie powierzchniowe wody wynosi 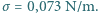 Dla ciśnienia atmosferycznego przyjąć wartość
Dla ciśnienia atmosferycznego przyjąć wartość 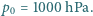
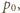 ciśnienie słupa wody
ciśnienie słupa wody 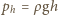 (
( 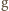 - przyspieszenie ziemskie,
- przyspieszenie ziemskie, 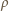 - gęstość wody) i ciśnienie wynikające z napięcia powierzchniowego
- gęstość wody) i ciśnienie wynikające z napięcia powierzchniowego 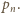 Przy powierzchni wody na ciśnienie w pęcherzyku składa się ciśnienie atmosferyczne
Przy powierzchni wody na ciśnienie w pęcherzyku składa się ciśnienie atmosferyczne 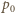 i ciśnienie wynikające z napięcia powierzchniowego
i ciśnienie wynikające z napięcia powierzchniowego 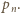
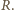 Jeżeli powiększymy jego promień o
Jeżeli powiększymy jego promień o 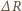 to powierzchnia wzrośnie o
to powierzchnia wzrośnie o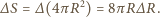
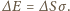 Powiększenie promienia pęcherzyka jest skutkiem wykonania pracy
Powiększenie promienia pęcherzyka jest skutkiem wykonania pracy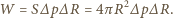
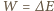 otrzymujemy na dodatkowe ciśnienie wyrażenie
otrzymujemy na dodatkowe ciśnienie wyrażenie 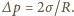
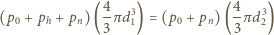
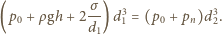
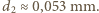 Zauważmy, że wkład od napięcia powierzchniowego jest znacznie mniejszy od ciśnienia atmosferycznego i hydrostatycznego i może być pominięty.
Zauważmy, że wkład od napięcia powierzchniowego jest znacznie mniejszy od ciśnienia atmosferycznego i hydrostatycznego i może być pominięty.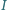 wypadkowego drgania powstałego w wyniku dodawania się dwóch fal elektromagnetycznych o takiej samej częstości i o natężeniach
wypadkowego drgania powstałego w wyniku dodawania się dwóch fal elektromagnetycznych o takiej samej częstości i o natężeniach 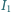 i
i 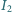 będzie równe sumie natężeń drgań składowych niezależnie od różnicy faz między nimi?
będzie równe sumie natężeń drgań składowych niezależnie od różnicy faz między nimi?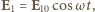 a drugiej
a drugiej 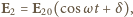 gdzie
gdzie 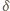 jest różnicą faz między drganiami. Drganie wypadkowe będzie dane wzorem
jest różnicą faz między drganiami. Drganie wypadkowe będzie dane wzorem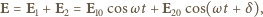
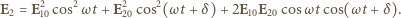
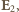 czyli
czyli
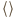 oznacza średnią względem czasu. Wyrażenie to będzie równe zero niezależnie od wartości przesunięcia fazowego
oznacza średnią względem czasu. Wyrażenie to będzie równe zero niezależnie od wartości przesunięcia fazowego 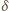 jeżeli iloczyn skalarny
jeżeli iloczyn skalarny 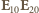 będzie równy zero, a to oznacza, że kierunki drgań muszą być względem siebie prostopadłe.
będzie równy zero, a to oznacza, że kierunki drgań muszą być względem siebie prostopadłe.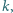 masę
masę 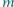 i długość
i długość 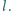 Okrąg zrobiony z tego kabla obraca się z prędkością kątową
Okrąg zrobiony z tego kabla obraca się z prędkością kątową 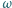 w płaszczyźnie poziomej wokół osi pionowej, przechodzącej przez środek okręgu. Wyznaczyć promień obracającego się pierścienia.
w płaszczyźnie poziomej wokół osi pionowej, przechodzącej przez środek okręgu. Wyznaczyć promień obracającego się pierścienia.
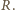 Rozważmy mały element tego okręgu o długości
Rozważmy mały element tego okręgu o długości 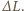 Jego masa to
Jego masa to 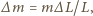 gdzie
gdzie 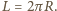 Na wydzielony element na jego końcach działają dwie siły naprężenia
Na wydzielony element na jego końcach działają dwie siły naprężenia 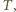 skierowane stycznie do okręgu. Ich wypadkowa
skierowane stycznie do okręgu. Ich wypadkowa 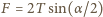 nadaje rozważanemu elementowi przyspieszenie dośrodkowe
nadaje rozważanemu elementowi przyspieszenie dośrodkowe 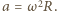 Równanie ruchu tego elementu ma postać
Równanie ruchu tego elementu ma postać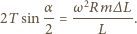
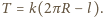 Uwzględniając, że kąt
Uwzględniając, że kąt 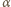 jest mały, czyli
jest mały, czyli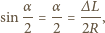
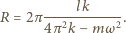

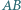 o masie
o masie 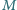 przyczepione jest wahadło matematyczne
przyczepione jest wahadło matematyczne 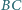 o masie
o masie  Punkt zawieszenia
Punkt zawieszenia 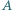 tego wahadła podwójnego drga harmonicznie wzdłuż linii poziomej z częstością
tego wahadła podwójnego drga harmonicznie wzdłuż linii poziomej z częstością 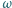 i małą amplitudą. Znaleźć długość nici dolnego wahadła, jeżeli górna nić przez cały czas pozostaje pionowa.
i małą amplitudą. Znaleźć długość nici dolnego wahadła, jeżeli górna nić przez cały czas pozostaje pionowa.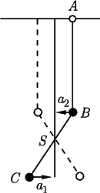
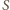 układu nie przemieszcza się w kierunku poziomym, a kulki w każdej chwili poruszają się w kierunkach przeciwnych. Stosunek ich przyspieszeń w kierunku poziomym wynosi
układu nie przemieszcza się w kierunku poziomym, a kulki w każdej chwili poruszają się w kierunkach przeciwnych. Stosunek ich przyspieszeń w kierunku poziomym wynosi 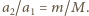 Oznaczmy szukaną długość dolnej nici przez
Oznaczmy szukaną długość dolnej nici przez 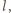 a odległość dolnej kulki od środka masy przez
a odległość dolnej kulki od środka masy przez 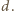 Z rysunku widać, że
Z rysunku widać, że 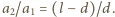 Z porównania wzorów na stosunki przyspieszeń otrzymujemy
Z porównania wzorów na stosunki przyspieszeń otrzymujemy 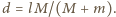 Ponieważ amplituda drgań punktu
Ponieważ amplituda drgań punktu 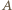 jest mała, przemieszczenia środka masy układu w kierunku pionowym również są małe i dolna kulka zachowuje się w przybliżeniu jak wahadło matematyczne o długości
jest mała, przemieszczenia środka masy układu w kierunku pionowym również są małe i dolna kulka zachowuje się w przybliżeniu jak wahadło matematyczne o długości 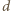 zawieszone w nieruchomym punkcie
zawieszone w nieruchomym punkcie 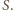 Częstość drgań tego wahadła jest taka sama jak częstość drgań punktu
Częstość drgań tego wahadła jest taka sama jak częstość drgań punktu 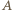 i wynosi
i wynosi 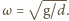 Stąd dolna nić ma długość
Stąd dolna nić ma długość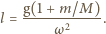
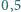 l powietrza. Skład wdychanego powietrza to (objętościowo) w
l powietrza. Skład wdychanego powietrza to (objętościowo) w 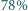 azot i
azot i 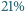 tlen, a wydychanego powietrza w
tlen, a wydychanego powietrza w 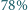 azot,
azot, 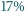 tlen i
tlen i 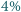 dwutlenek węgla.
dwutlenek węgla.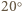 C (temperatura pokojowa) wynosi około 24 l (wszystkie gazy biorące udział w oddychaniu traktujemy jak gazy doskonałe). Ułamki objętościowe odpowiadają więc ułamkom molowym składu wdychanego i wydychanego powietrza. Biorąc pod uwagę masy molowe:
C (temperatura pokojowa) wynosi około 24 l (wszystkie gazy biorące udział w oddychaniu traktujemy jak gazy doskonałe). Ułamki objętościowe odpowiadają więc ułamkom molowym składu wdychanego i wydychanego powietrza. Biorąc pod uwagę masy molowe: 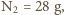
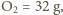
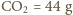 i fakt, że w jednym oddechu wymieniamy
i fakt, że w jednym oddechu wymieniamy 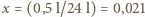 mola powietrza, otrzymujemy, że w każdym oddechu tracimy około
mola powietrza, otrzymujemy, że w każdym oddechu tracimy około 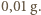 W ciągu 8 godzin snu daje to około 58 g.
W ciągu 8 godzin snu daje to około 58 g.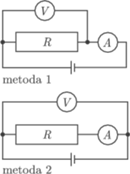
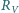 i amperomierz o oporze wewnętrznym
i amperomierz o oporze wewnętrznym 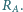 W celu wyznaczenia nieznanej wartości oporu
W celu wyznaczenia nieznanej wartości oporu 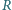 opornika możemy zestawić obwód pomiarowy na dwa różne sposoby (rysunek). Wykonując pomiary metodą 1, odczytaliśmy wartość prądu równą
opornika możemy zestawić obwód pomiarowy na dwa różne sposoby (rysunek). Wykonując pomiary metodą 1, odczytaliśmy wartość prądu równą 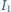 i napięcie równe
i napięcie równe 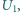 a pomiary metodą 2 dały wyniki
a pomiary metodą 2 dały wyniki 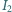 i
i 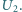 W jakich warunkach wartość obliczona na podstawie uproszczonego wzoru
W jakich warunkach wartość obliczona na podstawie uproszczonego wzoru 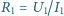 jest dokładniejszym przybliżeniem dokładnej wartości
jest dokładniejszym przybliżeniem dokładnej wartości 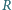 niż wartość
niż wartość 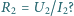 Zakładamy, że każdorazowo woltomierz poprawnie pokazuje różnicę potencjałów na jego zaciskach, a amperomierz poprawnie podaje wartość płynącego przezeń prądu.
Zakładamy, że każdorazowo woltomierz poprawnie pokazuje różnicę potencjałów na jego zaciskach, a amperomierz poprawnie podaje wartość płynącego przezeń prądu.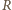 powinniśmy obliczać według wzorów:
powinniśmy obliczać według wzorów: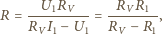
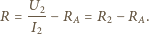
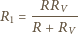
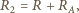
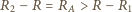
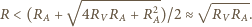
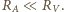
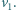 Lisa goni pies, którego prędkość ma stałą wartość
Lisa goni pies, którego prędkość ma stałą wartość 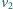 i skierowana jest cały czas na lisa. W chwili, gdy prędkości
i skierowana jest cały czas na lisa. W chwili, gdy prędkości 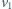 i
i 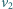 są do siebie prostopadłe, odległość między lisem a psem wynosi
są do siebie prostopadłe, odległość między lisem a psem wynosi 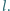 Jakie jest w tym momencie przyspieszenie psa?
Jakie jest w tym momencie przyspieszenie psa?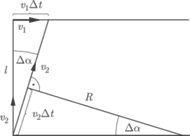
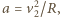 gdzie
gdzie 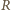 jest promieniem krzywizny toru w danym miejscu. W bardzo krótkim czasie
jest promieniem krzywizny toru w danym miejscu. W bardzo krótkim czasie 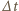 wektor prędkości psa obraca się o kąt
wektor prędkości psa obraca się o kąt 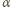 dany wzorem
dany wzorem 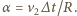 W tym samym czasie lis przebywa drogę
W tym samym czasie lis przebywa drogę 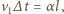 gdyż wektor prędkości psa skierowany jest cały czas na lisa. Stąd
gdyż wektor prędkości psa skierowany jest cały czas na lisa. Stąd 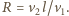 Szukana wartość przyspieszenia wynosi
Szukana wartość przyspieszenia wynosi 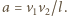
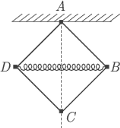
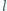 i lekkiej sprężyny o długości
i lekkiej sprężyny o długości 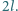 Pręty połączone są przegubowo za pomocą małych kulek o jednakowych masach. Układ zamocowany jest w punkcie
Pręty połączone są przegubowo za pomocą małych kulek o jednakowych masach. Układ zamocowany jest w punkcie  i znajduje się w polu ciężkości. W stanie równowagi pręty tworzą kwadrat. Znaleźć częstość małych drgań układu, przy których punkt
i znajduje się w polu ciężkości. W stanie równowagi pręty tworzą kwadrat. Znaleźć częstość małych drgań układu, przy których punkt  porusza się po linii pionowej.
porusza się po linii pionowej.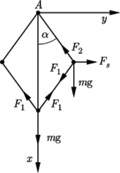
 Równania ruchu punktów
Równania ruchu punktów  i
i 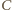 mają postać:
mają postać: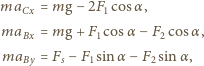
 jest masą przegubu,
jest masą przegubu, 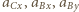 są przyspieszeniami punktów
są przyspieszeniami punktów 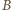 i
i 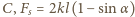 jest siłą sprężystości. Eliminując z tych równań siły reakcji
jest siłą sprężystości. Eliminując z tych równań siły reakcji 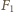 i
i 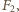 otrzymujemy
otrzymujemy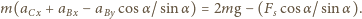
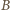 i
i 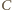 spełniają związki
spełniają związki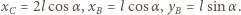
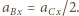 Dotychczasowe równania są słuszne dla dowolnego kąta
Dotychczasowe równania są słuszne dla dowolnego kąta 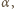 ograniczymy teraz nasze rozważania do małych wychyleń z położenia równowagi, gdy
ograniczymy teraz nasze rozważania do małych wychyleń z położenia równowagi, gdy 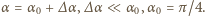 Wtedy
Wtedy 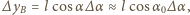
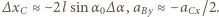 W rozważanym przybliżeniu lewa strona równania (1) ma postać
W rozważanym przybliżeniu lewa strona równania (1) ma postać 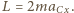 W stanie równowagi
W stanie równowagi 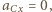 stąd
stąd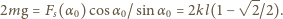
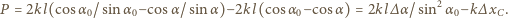
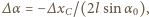 otrzymujemy równanie ruchu punktu
otrzymujemy równanie ruchu punktu 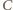 dla małych wychyleń z położenia równowagi:
dla małych wychyleń z położenia równowagi: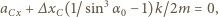
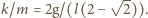 Szukana częstość drgań wynosi
Szukana częstość drgań wynosi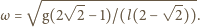
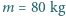 nabrał pełno powietrza do płuc
nabrał pełno powietrza do płuc 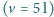 i wskoczył do wody. Z jakiej maksymalnej głębokości
i wskoczył do wody. Z jakiej maksymalnej głębokości 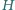 nurek może wypłynąć, nie wykonując żadnych ruchów? Objętość ciała nurka to
nurek może wypłynąć, nie wykonując żadnych ruchów? Objętość ciała nurka to 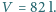
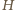 średnia gęstość nurka powinna być równa gęstości wody, a więc jego objętość powinna być równa
średnia gęstość nurka powinna być równa gęstości wody, a więc jego objętość powinna być równa 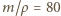 l, gdzie
l, gdzie 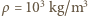 to gęstość wody. Zmniejszenie objętości ciała o wielkość
to gęstość wody. Zmniejszenie objętości ciała o wielkość 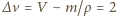 nastąpi - praktycznie biorąc - tylko w efekcie sprężenia powietrza w płucach, którego objętość zmaleje do
nastąpi - praktycznie biorąc - tylko w efekcie sprężenia powietrza w płucach, którego objętość zmaleje do 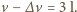 Przyjmując, że sprężenie następuje w stałej temperaturze, można zastosować prawo Boyle'a-Mariotte'a:
Przyjmując, że sprężenie następuje w stałej temperaturze, można zastosować prawo Boyle'a-Mariotte'a: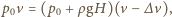
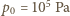 to ciśnienie atmosferyczne. Stąd otrzymujemy, że nurek może wypłynąć, nie wykonując żadnych ruchów, z głębokości nieco mniejszej od
to ciśnienie atmosferyczne. Stąd otrzymujemy, że nurek może wypłynąć, nie wykonując żadnych ruchów, z głębokości nieco mniejszej od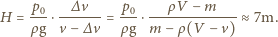
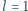 m doskonale odbijającą płytkę o masie
m doskonale odbijającą płytkę o masie 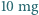 pada, prostopadle do jej powierzchni, wiązka światła laserowego. Jaka musiałaby być moc
pada, prostopadle do jej powierzchni, wiązka światła laserowego. Jaka musiałaby być moc 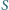 padającego światła, aby pod jego działaniem wahadło, którym jest zawieszona na nitce płytka, wychyliło się o kąt
padającego światła, aby pod jego działaniem wahadło, którym jest zawieszona na nitce płytka, wychyliło się o kąt 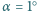 z położenia równowagi?
z położenia równowagi?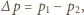 gdzie
gdzie 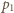 to pęd fotonu padającego, a
to pęd fotonu padającego, a 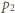 - pęd fotonu odbitego. Dla powierzchni doskonale odbijającej pędy
- pęd fotonu odbitego. Dla powierzchni doskonale odbijającej pędy 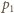 i
i 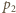 mają tę samą wartość
mają tę samą wartość 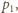 ale różnią się zwrotem, stąd zmiana pędu płytki wynosi
ale różnią się zwrotem, stąd zmiana pędu płytki wynosi 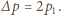 Energia
Energia 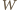 padających na płytkę w ciągu 1 s fotonów jest z definicji równa padającej na płytkę mocy
padających na płytkę w ciągu 1 s fotonów jest z definicji równa padającej na płytkę mocy 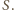 Ponieważ pęd
Ponieważ pęd 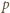 fotonu wiąże się z jego energią
fotonu wiąże się z jego energią 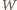 wzorem
wzorem 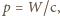 gdzie
gdzie  to prędkość światła, więc suma pędów fotonów padających na płytkę w czasie 1 s wynosi
to prędkość światła, więc suma pędów fotonów padających na płytkę w czasie 1 s wynosi 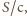 a pęd uzyskany przez płytkę w ciągu
a pęd uzyskany przez płytkę w ciągu 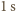 wynosi
wynosi 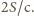 Zmiana pędu płytki w ciągu
Zmiana pędu płytki w ciągu 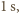 na mocy drugiej zasady dynamiki, jest równa działającej sile, więc
na mocy drugiej zasady dynamiki, jest równa działającej sile, więc 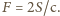 Ponieważ wychylenie wahadła wiąże się z siłą wzorem
Ponieważ wychylenie wahadła wiąże się z siłą wzorem 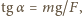 znajdujemy, że potrzebna moc to
znajdujemy, że potrzebna moc to 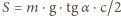 (przyjęliśmy, że dla
(przyjęliśmy, że dla 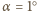 kąt padania wiązki nie zmienia się). Po podstawieniu danych liczbowych otrzymujemy
kąt padania wiązki nie zmienia się). Po podstawieniu danych liczbowych otrzymujemy 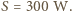 Dla wiązki światła laserowego o średnicy
Dla wiązki światła laserowego o średnicy 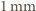 daje to gęstość mocy około
daje to gęstość mocy około 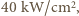 czyli z zakresu gęstości mocy stosowanych w technologiach cięcia i spawania metali.
czyli z zakresu gęstości mocy stosowanych w technologiach cięcia i spawania metali.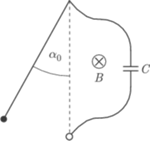
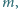 zawieszona na nieważkiej przewodzącej nici o długości
zawieszona na nieważkiej przewodzącej nici o długości 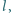 wykonuje małe drgania z amplitudą kątową
wykonuje małe drgania z amplitudą kątową 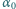 w płaszczyźnie pionowej, w jednorodnym polu magnetycznym o indukcji
w płaszczyźnie pionowej, w jednorodnym polu magnetycznym o indukcji 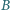 Linie pola magnetycznego są prostopadłe do płaszczyzny drgań wahadła. Gdy wahadło przechodzi przez położenie równowagi, podłączony zostaje do niego za pomocą cienkich, wiotkich przewodów kondensator o pojemności
Linie pola magnetycznego są prostopadłe do płaszczyzny drgań wahadła. Gdy wahadło przechodzi przez położenie równowagi, podłączony zostaje do niego za pomocą cienkich, wiotkich przewodów kondensator o pojemności 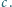 Czas kontaktu jest bardzo krótki i można przyjąć, że w tym czasie kondensator zostaje całkowicie naładowany. Znaleźć nową amplitudę kątową drgań wahadła.
Czas kontaktu jest bardzo krótki i można przyjąć, że w tym czasie kondensator zostaje całkowicie naładowany. Znaleźć nową amplitudę kątową drgań wahadła.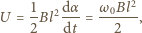
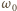 jest prędkością kątową wahadła w najniższym położeniu. Otrzymujemy ją z zasady zachowania energii, stosując przybliżenie małych kątów
jest prędkością kątową wahadła w najniższym położeniu. Otrzymujemy ją z zasady zachowania energii, stosując przybliżenie małych kątów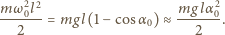
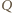 :
: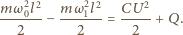
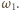 Czas kontaktu kulki z kondensatorem jest bardzo krótki, możemy więc przyjąć, że napięcie
Czas kontaktu kulki z kondensatorem jest bardzo krótki, możemy więc przyjąć, że napięcie 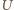 nie zmienia się podczas ładowania kondensatora. Źródło tego napięcia wykonuje zatem pracę
nie zmienia się podczas ładowania kondensatora. Źródło tego napięcia wykonuje zatem pracę 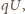 gdzie
gdzie 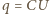 jest ładunkiem, do jakiego naładował się kondensator. Stąd
jest ładunkiem, do jakiego naładował się kondensator. Stąd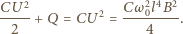
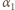 wahadła znajdujemy z równania
wahadła znajdujemy z równania 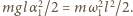 Uwzględniając (2), (3) i (4), dostajemy
Uwzględniając (2), (3) i (4), dostajemy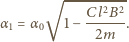
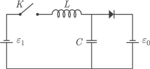
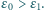 Jaki ładunek przepłynie przez źródło o sile elektromotorycznej
Jaki ładunek przepłynie przez źródło o sile elektromotorycznej 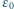 po zamknięciu klucza
po zamknięciu klucza 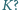 Zakładamy, że opór omowy cewki i opory wewnętrzne źródeł są równe zeru. Dioda jest idealna, czyli jej opór w kierunku przewodzenia wynosi zero, a w kierunku przeciwnym jest nieskończenie wielki. Przed zamknięciem klucza kondensator był nienaładowany.
Zakładamy, że opór omowy cewki i opory wewnętrzne źródeł są równe zeru. Dioda jest idealna, czyli jej opór w kierunku przewodzenia wynosi zero, a w kierunku przeciwnym jest nieskończenie wielki. Przed zamknięciem klucza kondensator był nienaładowany.
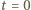 natężenie prądu płynącego przez cewkę i ładunek na kondensatorze są równe zeru. Spełnione są równania
natężenie prądu płynącego przez cewkę i ładunek na kondensatorze są równe zeru. Spełnione są równania
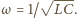 W obwodzie zachodzą drgania harmoniczne. Natężenie prądu płynącego przez cewkę osiąga maksymalną wartość, gdy znika jego pochodna po czasie, napięcie na kondensatorze równe jest wtedy sile elektromotorycznej źródła
W obwodzie zachodzą drgania harmoniczne. Natężenie prądu płynącego przez cewkę osiąga maksymalną wartość, gdy znika jego pochodna po czasie, napięcie na kondensatorze równe jest wtedy sile elektromotorycznej źródła 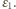 Kondensator ładuje się dalej kosztem energii pola magnetycznego w cewce. Gdy natężenie prądu
Kondensator ładuje się dalej kosztem energii pola magnetycznego w cewce. Gdy natężenie prądu 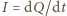 spada do zera, ładunek na kondensatorze osiąga maksymalną wartość
spada do zera, ładunek na kondensatorze osiąga maksymalną wartość 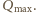 Zgodnie z zasadą zachowania energii mamy
Zgodnie z zasadą zachowania energii mamy 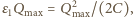 czyli maksymalne napięcie na kondensatorze wynosi
czyli maksymalne napięcie na kondensatorze wynosi 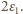
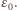 Gdy
Gdy 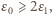 przez źródło o sile elektromotorycznej
przez źródło o sile elektromotorycznej 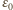 nie przepłynie żaden ładunek.
nie przepłynie żaden ładunek.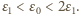 Gdy napięcie na kondensatorze osiąga wartość
Gdy napięcie na kondensatorze osiąga wartość 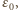 prąd płynie przez diodę kosztem energii pola magnetycznego w cewce zgodnie z równaniem
prąd płynie przez diodę kosztem energii pola magnetycznego w cewce zgodnie z równaniem 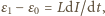 czyli natężenie prądu maleje liniowo w czasie. Do chwili, gdy jego wartość spadnie do zera, napięcie na kondensatorze nie zmienia się. Oznaczmy przez
czyli natężenie prądu maleje liniowo w czasie. Do chwili, gdy jego wartość spadnie do zera, napięcie na kondensatorze nie zmienia się. Oznaczmy przez 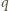 szukany ładunek przepływający przez źródło o sile elektromotorycznej
szukany ładunek przepływający przez źródło o sile elektromotorycznej 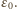 Od chwili zamknięcia klucza do chwili, kiedy przez diodę przestaje płynąć prąd, przez źródło
Od chwili zamknięcia klucza do chwili, kiedy przez diodę przestaje płynąć prąd, przez źródło 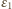 przepływa ładunek
przepływa ładunek 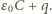 Bilans energetyczny dla całego procesu ma postać
Bilans energetyczny dla całego procesu ma postać 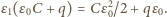 Stąd
Stąd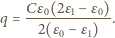
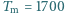 K, promień Słońca
K, promień Słońca 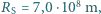 temperatura powierzchni Słońca
temperatura powierzchni Słońca 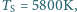 a stała Boltzmanna
a stała Boltzmanna 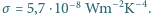
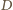 od jego środka wynosi:
od jego środka wynosi: 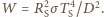 Dla uproszczenia dalszych obliczeń przyjmijmy, że możemy pominąć kątowe rozmiary Słońca. Wówczas ciało o promieniu
Dla uproszczenia dalszych obliczeń przyjmijmy, że możemy pominąć kątowe rozmiary Słońca. Wówczas ciało o promieniu  absorbuje moc
absorbuje moc 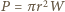 i, po osiągnięciu temperatury równowagi
i, po osiągnięciu temperatury równowagi 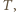 tę samą moc emituje. Mamy więc
tę samą moc emituje. Mamy więc 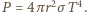 Meteoroid pozostaje w stanie stałym, gdy
Meteoroid pozostaje w stanie stałym, gdy 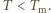 Oznacza to, że odległość od Słońca stałych meteoroidów żelaznych musi spełniać warunek:
Oznacza to, że odległość od Słońca stałych meteoroidów żelaznych musi spełniać warunek: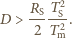
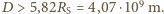 Nasze oszacowanie jest zaniżone, gdyż w tak małej odległości od Słońca poprawka wynikająca z faktu, że jest ono źródłem rozciągłym jest już dość znaczna - rozmiary kątowe Słońca "widziane" przez meteoroid wynoszą bowiem wówczas około
Nasze oszacowanie jest zaniżone, gdyż w tak małej odległości od Słońca poprawka wynikająca z faktu, że jest ono źródłem rozciągłym jest już dość znaczna - rozmiary kątowe Słońca "widziane" przez meteoroid wynoszą bowiem wówczas około 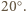
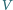 względem Ziemi takie odłamki mogą wchodzić do jej atmosfery. Przyjmij, że masa Słońca
względem Ziemi takie odłamki mogą wchodzić do jej atmosfery. Przyjmij, że masa Słońca 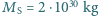 , odległość Ziemia-Słońce
, odległość Ziemia-Słońce 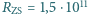 m, a stała grawitacji
m, a stała grawitacji 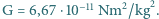
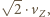 gdzie
gdzie 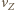 to prędkość, z jaką Ziemia obiega Słońce (
to prędkość, z jaką Ziemia obiega Słońce ( 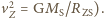 Maksymalna prędkość meteoroid-Ziemia wynosi więc
Maksymalna prędkość meteoroid-Ziemia wynosi więc 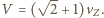 Po podstawieniu wartości liczbowych otrzymujemy
Po podstawieniu wartości liczbowych otrzymujemy 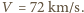
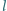 przyczepiono małą kulkę o masie
przyczepiono małą kulkę o masie 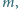 a do górnego końca rurkę w kształcie walca o wewnętrznym promieniu
a do górnego końca rurkę w kształcie walca o wewnętrznym promieniu 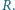 Masy pręta i rurki są zaniedbywalne. Rurka nasunięta jest luźno na nieruchomą, poziomą oś. Współczynnik tarcia między wewnętrzną powierzchnią rurki i osią jest równy
Masy pręta i rurki są zaniedbywalne. Rurka nasunięta jest luźno na nieruchomą, poziomą oś. Współczynnik tarcia między wewnętrzną powierzchnią rurki i osią jest równy 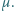 Dla jakich wartości kąta
Dla jakich wartości kąta 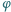 odchylenia pręta od pionu tak skonstruowane wahadło może znajdować się w równowadze?
odchylenia pręta od pionu tak skonstruowane wahadło może znajdować się w równowadze?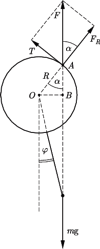
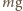 zaczepiona w środku kulki oraz siły reakcji
zaczepiona w środku kulki oraz siły reakcji 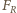 i tarcia
i tarcia 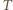 w punkcie
w punkcie 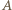 styczności osi z wewnętrzną powierzchnią rurki. Suma momentów tych sił względem dowolnego punktu wynosi zero, zatem proste, wzdłuż których działają siły, muszą się przecinać w jednym punkcie. Wynika stąd, że punkt
styczności osi z wewnętrzną powierzchnią rurki. Suma momentów tych sił względem dowolnego punktu wynosi zero, zatem proste, wzdłuż których działają siły, muszą się przecinać w jednym punkcie. Wynika stąd, że punkt 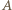 leży na przecięciu prostej pionowej, przechodzącej przez środek masy kulki z wewnętrzną powierzchnią rurki. Gdy środek kulki przemieszczony jest w prawo lub w lewo na odległość większą niż promień
leży na przecięciu prostej pionowej, przechodzącej przez środek masy kulki z wewnętrzną powierzchnią rurki. Gdy środek kulki przemieszczony jest w prawo lub w lewo na odległość większą niż promień 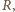 równowaga jest niemożliwa. Gdy kąt
równowaga jest niemożliwa. Gdy kąt 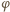 odchylenia wahadła od pionu jest maksymalny, tarcie statyczne osiąga największą możliwą wartość
odchylenia wahadła od pionu jest maksymalny, tarcie statyczne osiąga największą możliwą wartość 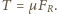 Ponieważ w stanie równowagi wypadkowa
Ponieważ w stanie równowagi wypadkowa 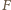 sił tarcia i reakcji skierowana jest pionowo w górę, zachodzi związek
sił tarcia i reakcji skierowana jest pionowo w górę, zachodzi związek 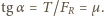 Odcinek
Odcinek 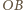 na rysunku możemy wyrazić przez kąty
na rysunku możemy wyrazić przez kąty 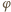 i
i 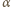 wzorem
wzorem 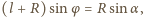 stąd
stąd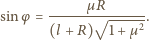
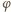 nie zależy od masy kulki. Dla
nie zależy od masy kulki. Dla 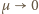 stan równowagi możliwy jest tylko dla pionowego położenia wahadła. Gdy
stan równowagi możliwy jest tylko dla pionowego położenia wahadła. Gdy 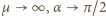 i
i 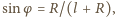 wtedy maksymalne odchylenie kulki w prawo dąży do
wtedy maksymalne odchylenie kulki w prawo dąży do 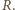 Gdy występuje tarcie w osi, wahadło może znaleźć się w równowadze także w położeniu odwróconym, kiedy kulka znajduje się powyżej osi.
Gdy występuje tarcie w osi, wahadło może znaleźć się w równowadze także w położeniu odwróconym, kiedy kulka znajduje się powyżej osi.
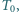 jednakowej w całym naczyniu, objętość gazu nad tłokiem jest
jednakowej w całym naczyniu, objętość gazu nad tłokiem jest 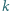 razy większa niż objętość gazu pod tłokiem. Jaki będzie stosunek tych objętości, gdy temperatura wzrośnie do wartości
razy większa niż objętość gazu pod tłokiem. Jaki będzie stosunek tych objętości, gdy temperatura wzrośnie do wartości 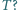
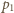 i
i 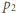 ciśnienia w dolnej i górnej części naczynia w temperaturze
ciśnienia w dolnej i górnej części naczynia w temperaturze 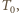 a przez
a przez 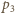 i
i 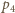 odpowiednie ciśnienia w temperaturze
odpowiednie ciśnienia w temperaturze 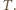 Różnica ciśnień związana jest z ciężarem tłoka i nie zależy od temperatury
Różnica ciśnień związana jest z ciężarem tłoka i nie zależy od temperatury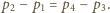
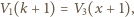
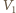 i
i 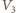 to początkowa i końcowa objętość gazu w dolnej części naczynia, a
to początkowa i końcowa objętość gazu w dolnej części naczynia, a  jest szukanym stosunkiem objętości w stanie końcowym. Masy gazu w obu częściach naczynia są takie same, z równań Clapeyrona wynikają więc związki
jest szukanym stosunkiem objętości w stanie końcowym. Masy gazu w obu częściach naczynia są takie same, z równań Clapeyrona wynikają więc związki 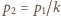 oraz
oraz 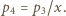 Podstawiając je do równania (1), otrzymujemy
Podstawiając je do równania (1), otrzymujemy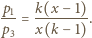
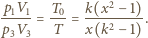
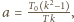 możemy napisać równanie kwadratowe na szukaną wielkość
możemy napisać równanie kwadratowe na szukaną wielkość 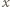 w postaci
w postaci 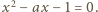 Dodatni pierwiastek tego równania ma postać
Dodatni pierwiastek tego równania ma postać 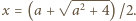 Dla
Dla 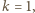 co odpowiada nieważkiemu tłokowi,
co odpowiada nieważkiemu tłokowi, 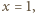 czyli objętości gazów nad i pod tłokiem są takie same. Dla dowolnego
czyli objętości gazów nad i pod tłokiem są takie same. Dla dowolnego 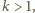 gdy temperatura dąży do nieskończoności, wartość
gdy temperatura dąży do nieskończoności, wartość 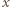 również dąży do 1. W bardzo wysokiej temperaturze ciśnienia gazów w obu częściach naczynia są na tyle duże, że wpływ siły ciężkości tłoka można pominąć.
również dąży do 1. W bardzo wysokiej temperaturze ciśnienia gazów w obu częściach naczynia są na tyle duże, że wpływ siły ciężkości tłoka można pominąć.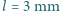 , a średnica tułowia jest równa szerokości skrzydła
, a średnica tułowia jest równa szerokości skrzydła 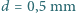 . Gęstość powietrza to
. Gęstość powietrza to 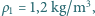 a średnia gęstość komara
a średnia gęstość komara 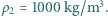
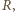 działającą na skrzydło, możemy oszacować, posługując się analizą wymiarową, przyjmując, że siła ta zależy od gęstości powietrza, prędkości jego strumienia oraz pola powierzchni prostopadłego do niego przekroju poprzecznego:
działającą na skrzydło, możemy oszacować, posługując się analizą wymiarową, przyjmując, że siła ta zależy od gęstości powietrza, prędkości jego strumienia oraz pola powierzchni prostopadłego do niego przekroju poprzecznego: 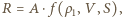 a współczynnik
a współczynnik 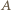 dla zakresu prędkości, z jakim mamy do czynienia, to około 1/2.
dla zakresu prędkości, z jakim mamy do czynienia, to około 1/2.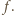 Założymy, że amplituda machnięć jest rzędu długości skrzydła
Założymy, że amplituda machnięć jest rzędu długości skrzydła 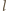 i że skrzydła opuszczają się płasko, a podnoszą się krawędzią tak, że opór powietrza przy podnoszeniu można pominąć. Średnia prędkość powietrza odrzucanego skrzydłami w dół wynosi
i że skrzydła opuszczają się płasko, a podnoszą się krawędzią tak, że opór powietrza przy podnoszeniu można pominąć. Średnia prędkość powietrza odrzucanego skrzydłami w dół wynosi 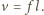 Posługując się analizą wymiarową, znajdujemy, że
Posługując się analizą wymiarową, znajdujemy, że 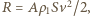 gdzie
gdzie 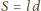 to powierzchnia skrzydła (współczynnik
to powierzchnia skrzydła (współczynnik 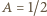 z warunków zadania). Siła unosząca
z warunków zadania). Siła unosząca 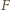 jest równa średniej czasowej siły oporu działającej na skrzydło, pomnożonej przez liczbę skrzydeł i podzielonej przez dwa, ponieważ opór powietrza działa na skrzydło tylko przy jego ruchu w dół. Stąd
jest równa średniej czasowej siły oporu działającej na skrzydło, pomnożonej przez liczbę skrzydeł i podzielonej przez dwa, ponieważ opór powietrza działa na skrzydło tylko przy jego ruchu w dół. Stąd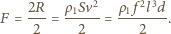
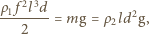
 to masa komara, g - przyspieszenie ziemskie. Ostatecznie
to masa komara, g - przyspieszenie ziemskie. Ostatecznie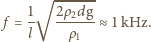
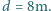 Czy uda mu się wznieść, jeżeli jego masa wraz z masą helikoptera wynosi
Czy uda mu się wznieść, jeżeli jego masa wraz z masą helikoptera wynosi 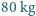 ? Przyjąć, że kolarz-amator przy długotrwałym wysiłku rozwija moc około 150 W. Masa cząsteczkowa powietrza to
? Przyjąć, że kolarz-amator przy długotrwałym wysiłku rozwija moc około 150 W. Masa cząsteczkowa powietrza to 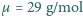 .
.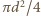 z prędkością
z prędkością 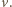 Jeżeli gęstość powietrza wynosi
Jeżeli gęstość powietrza wynosi 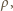 to w czasie
to w czasie 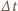 wirnik nadaje powietrzu o masie
wirnik nadaje powietrzu o masie 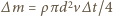 pęd
pęd 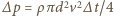 i energię kinetyczną
i energię kinetyczną 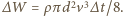 Aby helikopter się wzniósł, wirnik musi wytworzyć siłę ciągu równą ciężarowi helikoptera z pilotem:
Aby helikopter się wzniósł, wirnik musi wytworzyć siłę ciągu równą ciężarowi helikoptera z pilotem: 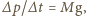 a potrzebna do tego moc wynosi
a potrzebna do tego moc wynosi 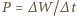 (g - przyspieszenie ziemskie). Korzystając z tego, że w warunkach normalnych objętość jednego mola gazu to
(g - przyspieszenie ziemskie). Korzystając z tego, że w warunkach normalnych objętość jednego mola gazu to 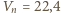 litra, znajdujemy, że gęstość powietrza wynosi
litra, znajdujemy, że gęstość powietrza wynosi 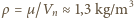 i otrzymujemy
i otrzymujemy